Задача 8

Прямолинейный проводник с длиной активной части 8 см и током 20 А находится в неоднородном магнитном поле (рис. 7). Магнитная индукция меняется по закону = с·х², где с = 0,1 Тл/м² , — орт оси OZ. Какая совершается работа при перемещении проводника вдоль оси ОХ из точки с координатой x₁= 0 см в точку с координатой х₂ = 20 см (рис. 8)? Какую скорость приобретет проводник при таком перемещении? Проводник расположен и перемещается перпендикулярно линиям индукции. Масса проводника 10 г.

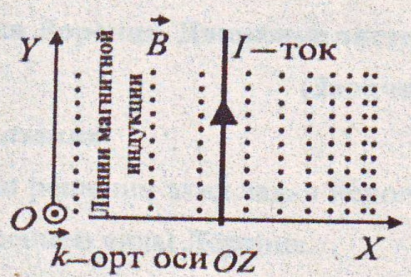
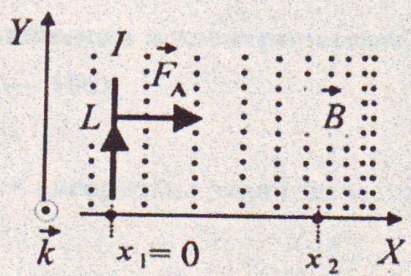
Рис.7 Рис.8

Д Прямая соединительная линия 20 ано: Решение

L= 0.08 м; I = 20 А По определению механическая работа

x₁= 0 см ; х₂ = 20 см А =

= с·х² В нашем случае α = 0°,

c = 0.1 Тл/м²

m = 0,01 кг F_A=1LB = IL· 0,1 · x² (рис. 8), поэтому

A,v-?

A=01IL

По теореме о кинетической энергии работа магнитного поля приводит к изменению кинетической энергии проводника, поэтому

А=

Ответ: А = 4,3·10^-4Дж; v = 0,3 м/с.

4. Сила Лоренца. Движение частиц в магнитном и электрическом полях. (Задачи № 75 —100)

Указания

При решении этих задач используются алгоритмы задач по механике с добавлением силы Лоренца.

Задача 9

Альфа-частица c кинетической энергией К = 500 эВ, влетает в однородное магнитное иоле перпендикулярно его силовым линиям, Индукция магнитного поля В = 0,1 Тл. Найти: 1) силу, действующую на частицу; 2) радиус окружности, по которой движется частица; 3) период обращения частицы.

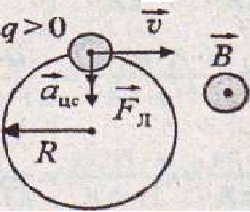
Рис.9

Д ано: Решение

К = 500 эВ = Зная кинетическую энергию альфа-частицы, определим ее скорость v:

= 1,6·10^-19·500 Дж К= (1)

В = 0,1 Тл где m — масса альфа-частицы.

F_л-?R - ?Т -?

На движущуюся частицу с зарядом q в магнитном поле действует сила Лоренца (рис. 9)

F_л = qv B sinα

направленная всегда перпендикулярно скорости частицы (правило левой руки):. В нашем случае угол между вектором скорости частицы и вектором магнитной индукции α = π/2, следовательно:

F_л = (2)