Задача 4

Б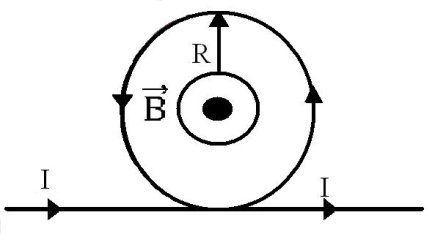 есконечно длинный провод образует круговую петлю, касательную к проводу. По проводу течет ток 5 А. Найти радиус петли, если известно, что индукция магнитного поля в центре петли равна 5·10 ^-5 Тл.

Рис.3

Дано; Решение

I= 5 А Индукция магнитного поля в центре петли равна векторной сумме индукции

В = 5·10^-5 Тл прямого тока и индукции кругового тока = + , где В₁ = ,

R-? В₂=

По правилу буравчика и параллельны, поэтому В =B₁ + В_2..

Таким образом, B =

Отсюда R=

Вычисления: R = ≈ 8, 3 • 10^-2 (м).

Ответ: R = 8, 3· 10^-2 м.

Задача 5

Два круговых витка расположены под углом 30° так, что их центры совпадают. Радиус каждого витка 2 см и токи, текущие по виткам I₁=I₂=I = 5 A. Найти индукцию магнитного поля в центре витков.

Рис.4

Д ано: Решение

R₁ = R₂ = R = 2 см Индукция магнитного поля в центре петли равна векторной сумме ин-

I₁ = I₂ = I = 5 А дукции кругового тока I₁ и индукции кругового тока I₂ (рис. 4)

α = 30° = + ,

B -? где В₁ = , и В₁ = , .

Направления и , определяемые по правилу буравчика, перпендикулярны, поэтому

.

Таким образом,

или .

Вычисления: ≈0,22 ·10^-3 (Тл).

Ответ: В= 2,2·10^-4 Тл.

3. Сила Ампера. Работа тока в магнитном поле. (Задачи №51 —75)

Указания

При решении этих задач используются алгоритмы задач по механике с добавлением силы Ампера, а также формулы механической работы:

A= , где F_A – сила Ампера или A= =I (Ф₂ – Ф₁),

где Ф₁— магнитный поток в начальном состоянии; Ф₂ — в конечном состоянии.

Задача 6

Между полюсами магнита подвешен горизонтально на двух невесомых нитях прямой проводник длиной 0,4 м и массой 10 г. Индукция однородно­го магнитного поля равна 0,05 Тл и перпендикулярна к проводнику. На какой угол от вертикали отклонятся нити, поддерживающие проводник, если по нему пропустить ток 5 А?

Рис.5

Д ано: Решение

L = 0,4 м

m = 0,01 кг На проводник действуют три силы: m — сила тяжести, — сила

В = 0,05 Тл натяжения нити, F_A-ILB — сила Ампера, действующая со стороны

I= 5 А магнитного поля на проводник длиной L с током I, направление которого

α =? перпендикулярно направлению магнитной индукции.

По условию равновесия в проекциях на ось X:

F_A - Тsinα = 0 => Тsinα = F_A,

в проекциях на ось Y:

Т cosα - mg = 0 =>T cosα = mg.

Разделив первое уравнение на второе, получим tgα = .

=> α =arctg1 = 45°.

Ответ: α = 45°.

Задача 7

И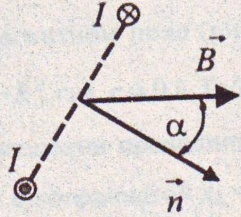 з проволоки длиной 20 см сделан квадратный контур, который помещен в магнитное поле с индукцией 0,1 Тл. Нормаль к контуру составляет угол 45^° с направлением поля. Определить вращающий момент, действующий при силе тока 2 А, и работу, которую надо совершить, чтобы расположить плоскость контура параллельно направлению магнитной индукции.

Рис.6

Д ано: Решение

L = 0,2 м Момент силы, действующей на контур с током в магнитном поле, определяется

I= 2 A формулой:

В = 0,1 Тл M = ISBsinα,

α= 45°; где S — площадь контура; α— угол между вектором магнитной индукции и

М, Aст. - ? нормалью к поверхности контура.

В нашем случае S = , α= 45°.

=> М = ISBsinα = 3А∙0,0025м² 0,1Тл =3_,5·l0^-4 Н·м.

Механическая работа контура с током в магнитном поле, определяется формулой:

:А =I(Ф₂ – Ф₁),

где Ф₁ — магнитный поток в начальном состоянии; Ф₂ — в конечном состоянии. В нашем случае Ф₁= BScos45˚, Ф₂= BScos90˚=0.

А = -IBScos45˚= -2А∙0,1Тл∙0,0025м² = - 3,5 • 10^-4 Дж.

Работа сторонних сил имеет знак, противоположный знаку работы контура с током. Поэтому, А_ст.= 3,5·10^-4 Дж.

Ответ: М = 3_,5·l0^-4 Н·м; А_ст.= 3,5·10^-4 Дж.