Раздел «Электромагнитная индукция» Краткая теория

Элементарный магнитный поток dФ через элемент по­верхности dS определяется формулой:

dФ = B S cosα,

где α — угол между единичным вектором нормали к поверхности, ох­ватываемой контуром, и вектором магнитной индукции .

Полный магнитный поток через поверхность S:

.

Механическая работа, совершаемая при перемещении контура с током в магнитном поле:

A =

При конечном изменении потока и постоянном токе I:

A=I(Ф₂-Ф₁).

где Ф₁ — магнитный поток в начальном положении контура; Ф₂ — в конечном положении.

Индуктивность соленоида L:

L=μ₀ ·n²l∙ S= μ₀ ·n²V

где μ₀ = 4π • 10^-7 Гн/м - магнитная постоянная; l - длина соленоида; S - площадь поперечного сечения соленоида; n = ─ число витков на единицу длины, V = l∙ S — объем соленоида.

Индукция магнитного поля в соленоиде направлена вдоль оси соленоида:

В = μ₀ n I = ,

где I ─ сила тока.

Индукция магнитного поля в веществе :

= μμ₀ ,,

где μ – относительная магнитная проницаемость среды; ─ напряженность магнитного поля.

Закон электромагнитной индукции: ЭДС индукции ε пропорциональна скорости изменения магнитного потока Ф сквозь поверхность, охватываемую контуром:

.

Среднее значение ЭДС индукции:

,

где ΔФ ─ изменение магнитного потока за время Δt.

Закон самоиндукции: ЭДС самоиндукции ε_с пропорциональна скорости изменения силы тока / в контуре:

.

где L - индуктивность контура.

Среднее значение ЭЛС самоиндукции:

,

где ΔI ─ изменение силы тока в контуре за время Δt.

Закон взаимной индукции: ЭДС взаимной индукции во втором контуре ε₂ пропорциональна скорости изменения силы тока I₁ в первом контуре:

.

где L₁₂ - взаимная индуктивность контуров.

Энергия магнитного поля W контурас током:

,

где L - индуктивность контура.

Плотность энергии магнитного поля w:

,

где и - индукция и напряженность магнитного поля.

Мгновенное значение силы тока I в цепи, содержащей ЭДС ε, со­противление R и индуктивность L через время t после замыкания цепи:

,

а при размыкании цепи:

где I₀ ─ значение силы тока в цепи при t=0; t─ время с момента размыка­ния цепи.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. Проводник длиной l помещен в магнитное поле с индукцией В. Концы проводника замкнуты гибким проводом, находящимся вне поля. Со­противление всей цепи R. Какую мощность необходимо затратить, чтобы двигать проводник перпендикулярно линиям индукции со скоростью V?

РЕШЕНИЕ

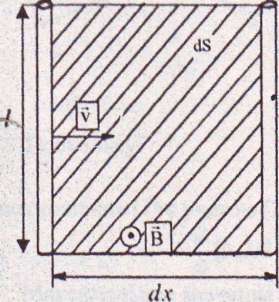
Мощность N, затраченная на пе­ремещение проводника, числен­но равна мощности индуциро­ванного в этом проводнике тока:

N = (1)

где R - электрическое сопротив­ление цепи; ε ─ ЭДС индукции, равная:

.

Здесь dФ - изменение магнитного потока при движении проводника за интервал времени dt, то есть:

dФ = BdS = Bldx,

где dS = Idx- площадь, очерченная проводником. Учитывая, что:

V = ,

получаем: dx=Vdt,

Отсюда: ε=-BIV (2)

С учетом (2) соотношение (1) принимает вид:

2. Определить максимальное значение ЭДС, которая возникает в замкнутом контуре площадью S, вращающемся с частотой ν в магнитном поле напряженностью H.

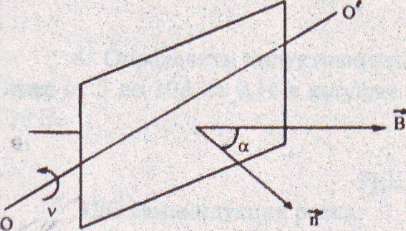РЕШЕНИЕ

Согласно закону электро­магнитной индукции, ЭДС индукции равна

(1)

где Ф - поток магнитной индук­ции сквозь контур, равный:

Ф=BScosα= BScos(2πvt) (2)

Здесь учтено, что:

α = ωt= 2πvt .

Поскольку: В = μ₀H , (3)

то соотношение (1) с учетом (2) и (3) принимает вид:

ε =

Максимальное значение ЭДС индукции:

ε₀ = 2πv μ₀H S .

3. Сколько витков N имеет соленоид, диаметр которого D и индук­тивность L, если при силе тока I индукция магнитного поля внутри соле­ноида равна В?

РЕШЕНИЕ

Индуктивность соленоида: L (1)

где l -длина; S- площадь поперечного сечения соленоида.

Подставляя площадь круга:

S =

в формулу (1), получаем: : L (2)

Индукция магнитного поля внутри соленоида:

B= (3)

Решая систему уравнений (2) и (3) относительно N, получаем:

.

4. Определить индуктивность катушки, если при изменении в ней тока от 5 до 10А за 0,1с в катушке возникает ЭДС самоиндукции, равная 10 В.

РЕШЕНИЕ

ЭДС самоиндукции равна: .

Знак “-” говорит о том, что, по правилу Ленца, индукционный ток препятствует любым изменениям исходного тока. Поэтому в численных расчетах его можно не учитывать.

Отсюда:

.

Ответ:L = 0,2 Гн.

5. Две катушки имеют взаимную индуктивность L_{12 =} 0,005 Гн. В первой катушке сила тока изменяется по закону I=I₀sinωt, где I₀=10А; ω=2π/T; Т= 0,02с. Найти: 1) зависимость от времени ЭДС, индуцируемой во вто­рой катушке; 2) наибольшее значение этой ЭДС.

РЕШЕНИЕ

Поскольку в первой катушке сила тока I=I₀sinωt изменяется со вре­менем, то во второй катушке, согласно закону электромагнитной индук­ции, возникает ЭДС, равная:

.

Учитывая, что ω=2π/T, найдем наибольшее значение ЭДС индук­ции во второй катушке:

ε₀ = .

Ответ:ε₀ = 15,7 В.

6.На стержень из немагнитного материала длиной 50 см и сечением 2 см² намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию магнитного поля внутри соленоида, если сила тока в обмотке равна 0,5 А.

РЕШЕНИЕ

Энергия магнитного поля соленоида с индуктивностью L, по обмот­ке которого течет ток I, выражается формулой:

.

Индуктивность соленоида с немагнитным сердечником равна:

L=μ₀n²Sl.

Объединив две эти формулы, получим:

W=

Ответ:W = 6, 28·10^-5 Дж.