2.3 Определение допускаемых напряжений изгиба

Предел изгибной выносливости:

- для колеса 2

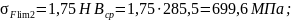
- для шестерни 1 по таблице 2.3

Коэффициенты запаса прочности: для зубчатого колеса 2 с однородной структурой материала (т.о. улучшение) и для шестерни 1 с поверхностным упрочнением (т.о. улучшение и закалка ТВЧ) S_F = 1,7.

Базовое число циклов нагружений при расчете на изгибную выносливость N_FG = 4 10⁶.

Коэффициент долговечности

где q = 6 для улучшенных зубчатых колес и q= 9 для закаленных и поверхностно-упрочненных зубьев.

принимаем

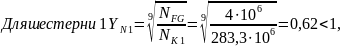
принимаем

Допускаемые напряжения изгиба:

2.4 Определение межосевого расстояния

Коэффициент ширины колеса относительно межосевого расстояния по рекомендации [1] при симметричном расположении колес относительно опор ψ_ba = 0,4.

Коэффициент ширины относительно диаметра шестерни

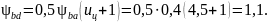
Коэффициент неравномерности распределения нагрузки по длине контактных линий (коэффициент концентрации нагрузки) при твердости шестерни 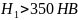и колеса (вариант т.о. 2)

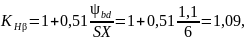
где – номер схемы (1, 2, 3…7) расположения колес в редукторе относительно опор по рисунку 2.4 [1].

Коэффициент межосевого расстояния для косозубых передач K_a = 430.

Межосевое расстояние

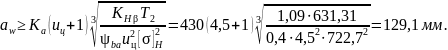
Принимаем a_w = 135 мм.

2.5 Предварительные основные размеры колеса

Делительный диаметр

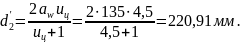
Ширина (ширину колеса принимают равной рабочей ширине венца зубчатой передачи)

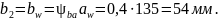
По ряду нормальных линейных размеров принимаем b₂ = 55 мм.

2.6 Определение модуля передачи

Модуль передачи

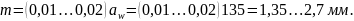
По стандартному ряду модулей принимаем m = 2 мм.

2.7 Определение угла наклона зубьев колес и суммарного числа зубьев

Минимальный угол наклона зубьев косозубых колес

Суммарное число зубьев

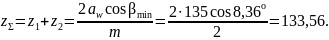
Полученное значение округляем в меньшую сторону до целого числа z_Σ = 133.

Действительное значение угла зубьев

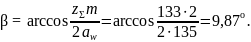
Для косозубых колес рекомендуемое значение угла наклона зубьев β = 8…20^о.

2.8 Определение чисел зубьев шестерни и колеса

Число зубьев шестерни

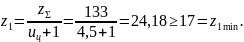
Принимаем z₁ = 24.

Число зубьев колеса

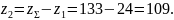
2.9 Определение фактического передаточного числа

Фактическое передаточное число

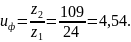
Отклонение от заданного передаточного числа

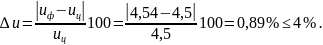
2.10 Размеры колес

Делительные диаметры:

- шестерни 1

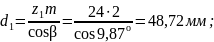
- колеса 2

Диаметры окружностей вершин 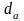и впадин зубьев:

- шестерни 1

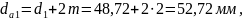
- колеса 2

Ширина шестерни 1

По ряду нормальных линейных размеров принимаем b₂ = 60 мм.

2.11 Определение сил, действующих в зацеплении

Силы в зацеплении:

- окружная

- радиальная

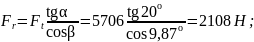
- осевая

2.12 Проверка зубьев колес по контактным напряжениям

Окружная скорость колеса

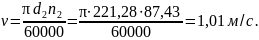
По таблице 2.5 [1], в зависимости от окружной скорости колеса, принимаем 8-ю степень точности зубчатой передачи.

Коэффициент распределения нагрузки между зубьями для косозубых передач

где n_ст – число соответствующее степени точности, ;

C – коэффициент, С = 0,12 при твердости поверхностей зубьев шестерни и колеса H₁ и H₂ > 350 НВ, С = 0,06 при H₁ и H₂ 350 НВ или H₁ > 350 НВ, а H₂ < 350 НВ.

Тогда

По таблице 2.6 [1] принимаем коэффициент, учитывающий динамическую нагрузку, K_Hv = 1,02.

Коэффициент, учитывающий механические свойства сопряженных зубатых колес, для стальных колес Z_E = 190.

Коэффициент торцового перекрытия для передач без смещения исходного контура

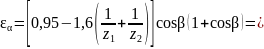
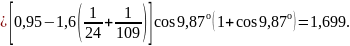
Коэффициент, учитывающий суммарную длину контактных линий, для косозубых передач

Коэффициент, учитывающий форму сопряжений поверхностей, для косозубых передач, выполненных без смещения исходного контура

Расчетное контактное напряжение в зацеплении

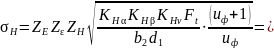
где [σ]_H = 722,7 МПа.

Условие прочности выполняется.