З акон Паскаля

Рассмотрим две частицы жидкости, из которых одна распложена в точке 1 внутри объёма жидкости на высоте z от произвольно выбранной плоскости сравнения О-О, а другая находится в точке 2 на поверхности жидкости – на высоте z₀ от той же плоскости;

p и p₀ – давления в точках 1 и 2.

Согласно предыдущему уравнению

или ,

z – высота расположения точки над плоскостью сравнения (нивелирная высота);

- статический напор (или пьезометрический напор).

Следовательно, согласно основному уравнению гидростатики, сумма нивелирной высоты и статического напора есть величина постоянная.

Основное уравнение гидростатики представляет собой частный случай закона сохранения энергии и может быть сформулирован и так: общая удельная потенциальная энергия (удельная потенциальная энергия положения z и удельная потенциальная энергия давления ) во всех точках покоящейся жидкости есть величина постоянная.

z₀ - z = h - глубина погружения точки.

Уравнение можно записать и в другой форме:

или

.

Это есть закон Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости передаётся одинаково всем точкам её объёма.

Действительно, при изменении давления p₀ в точке z₀ на какую-либо величину давление p во всякой другой точке z жидкости изменится в соответствии с последним уравнением на ту же величину.

Практические приложения основного уравнения гидростатики

Основное уравнение гидростатики имеет ряд важных практических приложений. Рассмотрим наиболее важные из них.

1. Принцип сообщающихся сосудов и его использование.

а) жидкости с одинаковой плотностью

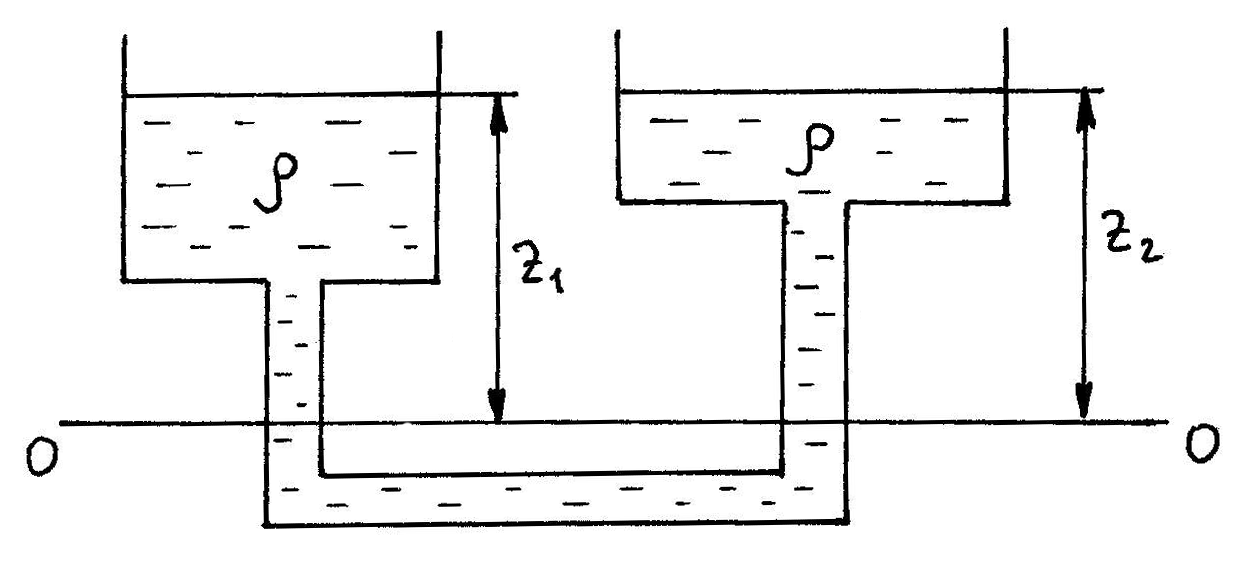
для левого сосуда

,

для правого сосуда

.

При равновесии для каждой точки давление одинаково в любом направлении (в противном случае происходило бы перемещение жидкости). Следовательно,

или z₁ = z₂.

Аналогичный вывод может быть сделан для двух закрытых сообщающихся сосудов, в которых давления над свободной поверхностью жидкости одинаковы.

Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни её располагаются на одной высоте независимо от формы и поперечного сечения сосудов.

Э тот принцип используется, в частности, для измерения уровня жидкости в закрытых аппаратах с помощью водомерных стёкол.

б) жидкости с разной плотностью

Аналогично предыдущему получим

или

,

или ,

то есть высоты уровней разнородных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей.

в) сосуды заполнены одной жидкостью (ρ), но давления над уровнем жидкости в них неодинаковы

,

откуда разность уровней жидкости в сосудах

.

Это уравнение применяют при измерении давлений или разности давлений между различными точками с помощью дифференциальных U-образных манометров.

Условия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных аппаратах.