Линейная (относительно   и  ) часть полного приращения функции называется полным дифференциалом и обозначается  : 

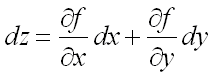
9. Двойной интеграл. Определение и свойства.

Двойной интеграл - это интеграл от функции двух переменных, который вычисляется в некоторой области переменных. 

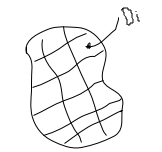
Определение: если независимо от способа дробления области D на N частей Di и независимо от выбора точек (x_i, y_i) существует и конечен предел интегральной суммы σ при ранге дробления λ → 0

то его называют двойным интегралом от функции f(x;y) в области D.

Свойства двойного интеграла.

1) Если f(x;y) непрерывна в области D, то она там интегрируема.

2) Если f(x;y) интегрируема в области D, то для любой с-сonst, функция сf(x;y) также интегрируема в области

3) Если функции f(x;y) и g(x;y) интегрируются в области D, то функция f(x;y)+g(x;y) также интегрируема в области D

Обратное неверно!

4) Пусть функция f(x;y) интегрируема в области D и пусть область D разбита на две подобласти D₁ и D₂, в пересечении которых пусто:

Геометрический смысл двойного интеграла: при неотрицательной функции f(x,y), двойной интеграл по области D представляет из себя объем криволинейного цилиндра, который построен на области D и ограничен сверху поверхностью z=f(x,y).

Вопрос 10

Выражение в правой части называется повторным интегралом.

Пусть область D задана в виде  . Эта область снизу ограничена прямой  , сверху -  , слева кривой  , справа кривой  . Двойной интеграл от функции   по такой области вычисляется по формуле

Равенство повторного и двойного интегралов

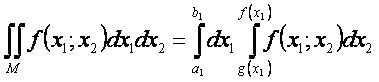
Вопрос 11

Связь между двойными и повторными интегралами

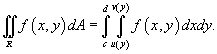
16.Криволинейный интеграл II-го рода. Определение, свойства и вычисление.

Если существует конечный предел при  интегральной суммы  , не зависящий от способа разбиения кривой на отрезки и выбора точек Mi, то от называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается

                     .      

Если вдоль плоской кривой   с концевыми точками А и В. Определена векторная функция 

Произведем дробление кривой АВ на N частей произвольным образом, но так

Определение: если независимо от способа дробления кривой АВ на N частей точек   и не зависимо от способа выбора точек   дуге  существует и конечен предел интегрирования суммы   при 

Специальные свойства криволинейного интеграла второго рода

1) Из определения следует, что если кривая АВ- отрезок прямой параллельный напр. оси ох, то

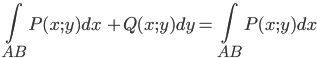
2) Из определения следует, что

Линейность:

2. Аддитивность:

3. 

16. приложенеие интегралов Вычисление площадей

Объем тела

Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой

лощадь поверхности

Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой

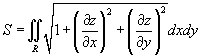
Центр тяжести плоской фигуры

Если 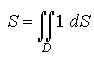    ,   то координаты х_c и у_c центра С находятся так:

центр масс и моменты инерции кривой

Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности ρ (x,y,z). Тогда координаты центра масс кривой определяются формулами

где

− так называемые моменты первого порядка.  Моменты инерции относительно осей Ox, Oy и Oz определяются формулами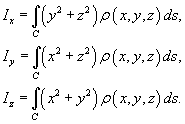

Работа поля

Работа при перемещении тела в силовом поле   вдоль кривой C выражается через криволинейный интеграл второго рода

Длина кривой 

     Масса кривой