4) Третий закон Ньютона.

Третий закон Ньютона: Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.

Это означает, что если на тело А со стороны тела В действует сила   ,  то одновременно на тело В со стороны тела А будет действовать сила   ,причем      = -  .

  

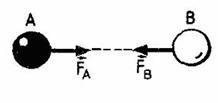
Используя второй закон Ньютона, можно  записать:

 ,

Отсюда следует, что

т. е. отношение модулей ускорений    и     взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил. Более массивное тело получает меньшее ускорение, а легкое - большее.

Важно понимать, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому они не могут уравновешивать друг друга.

5) Следствия из законов Ньютона

Законы Ньютона представляют собой систему взаимосвязанных законов, которые позволяют глубже понять сущность понятий силы и массы.  Следствия из законов:

1. Сила является мерой воздействия, оказываемого на данную частицу со стороны других тел, и с увеличением расстояния до них убывает, стремясь к нулю.

То, что сила является мерой воздействия со стороны окружающих частику тел, следует из того, что она зависит от состояния этих тел  и при этом определяет ускорение данной частицы:   . Убывания действующей силы до нуля при неогра­ниченном удалении от частицы окружающих ее тел  является следствием первого и второго законов Ньютона. Так как, со­гласно первому закону Ньютона, бесконечно удаленная от всех тел

частица имеет нулевое ускорение   . Согласно второму закону Нью­тона   Поэтому при    и сила   .

2. Сила, с которой сразу несколько тел действует на данную частицу, равна сумме сил, с которыми эти тела действуют на нее по отдельности:

Это утверждение  называется принципом  независимости  взаимодействий. С учетом этого принципа второй закон Ньютона записы­вается в виде:

Сумму сил, стоящую в правой части этого закона, называют равнодействующей силой.

Принцип независимости взаимодействий иначе называют принципом суперпозиции сил.

3. Сумма всех внутренних сил, действующих в любой сис­теме, всегда равна нулю.

Под внутренними понимают те силы, которые действуют между телами самой рассматриваемой системы.

Внутренние силы не способны привести в движение систему тел как целое. Действительно, для этого нужно было бы сообщить ускорение, а ускорение, как это следует из второго закона Ньютона, могут сообщить системе лишь те силы, сумма ко­торых отлична от нуля.

4. Отношение модулей ускорений, полученных двумя те­лами в результате взаимодействия друг с другом, равно обратному отношению их масс:

4. Реактивная тяга — сила, возникающая в результате взаимодействия двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающей кинетической энергией

Максимально достижимая скорость зависит в первую очередь от скорости истечения газов из сопла, которая в свою очередь зависит прежде всего от вида топлива и температуры газовой струи. Чем выше температура, тем больше скорость. Значит, для ракеты нужно подбирать самое калорийное топливо, дающее наибольшее количество теплоты. Отношение массы топлива к массе ракеты в конце работы двигателя (т.е. по существу к весу пустой ракеты) называется числом Циолковского.

Основной вывод состоит в том, что в безвоздушном пространстве ракета разовьёт тем большую скорость, чем больше скорость истечения газов и чем больше число Циолковского.

Движения тел переменной массы. Знание закона сохранения импульса во многих случаях дает возможность найти результат взаимодействия тел, когда значения действующих сил неизвестны.

Рассмотрим в качестве примера действие реактивного двигателя. При сгорании топлива в камере сгорания ракеты образуются газы, нагретые до высокой температуры. При действии двигателя в течение короткого интервала времени t из сопла ракеты выбрасываются со скоростью u относительно ракеты горячие газы массой m. Ракета и выбрасываемые ее двигателем газы взаимодействуют между собой. На основании закона сохранения импульса при отсутствии внешних сил сумма векторов импульсов взаимодействующих тел остается постоянной.

До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю:

где m - масса ракеты, V - изменение скорости ракеты, m - масса выброшенных газов, u - скорость истечения газов.

Отсюда для векторов импульса получаем:

Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:

или

Произведение массы ракеты m на ускорение ее движения a по определению равно силе, вызывающей это ускорение:

Таким образом, мы показали, что реактивная сила тяги Fp равна произведению скорости u движения выбрасываемых газов относительно ракеты на секундный расход топливаm/t.

Реактивная сила тяги Fp действует со стороны газов на ракету и направлена в сторону, противоположную направлению истечения газов.

Выражение 

есть уравнение динамики тела переменной массы для случая, когда внешние силы равны нулю. Если же на ракету, кроме реактивной силы Fp, действует внешняя сила F, то уравнение динамики движения примет вид:

Это уравнение получено профессором Петербургского университета  И. В. Мещерским и носит его имя.

Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами F, действующими на тело, но и реактивной силой Fp, обусловленной изменением массы движущегося тела:

Ракета. Система двух тел. Корпус топлива. Корпус - труба с одним открытым концом для выхода отработанных газов. На хвосте ставят сопла (трубки) для направленного выброса газов с большой скоростью. Топливо - сложное горючее, которое при сжигании превращается в газ большой температуры и большого движения.

V ракеты зависит от m топлива и самой ракеты, а также от V выбросов газов.

В данной формуле не учитывается сопротивление воздуха и F_пр к Земле.

На самом деле выброс газов происходит не мгновенно, а постепенно. Если учесть все условия, то топлива надо брать во много раз больше.

Чтобы сообщить кораблю первую космическую скорость, то

m_т >m_об= в 55 раз

5.

Консервативные и неконсервативные силы

Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное.

 Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

 

К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное.

Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

                    Потенциальная энергия.

 

Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил.

Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.

Е_П1 - Е_П2 = Е_П = А_12конс, .

 

Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.

 

.

Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.

Свойства потенциальной энергии.

1. Потенциальная энергия является конечной, однозначной, непрерывной

функцией механического состояния системы.

2. Численное значение потенциальной энергии зависит от выбора уровня с нулевой потенциальной энергией.

Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии:

 

,

 

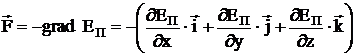причем

,  ,  .

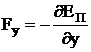Примеры потенциальной энергии:

1)  – потенциальная энергия тела массой m, поднятого на высоту h относительно нулевого уровня энергии в поле силы тяжести;

 

2)                    – потенциальная энергия упругого деформированного тела, х – деформация тела.

 

 

                                          Потенциальные кривые.

 

Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является функцией лишь одной переменной (например, координаты х), т. е. П=П (х). График зависимости потенциальной энергии от некоторого аргумента назы­ваетсяпотенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.

Будем рассматривать только консервативные системы, т. е. системы, в которых взаимные превращения механической энергии в другие виды отсутствуют. Тогда справедлив закон сохранения энергии в форме

 

Рассмотрим графическое пред­ставление потенциальной энергии для тела в однородном поле тяжести и для упругодеформированного тела.

Потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, согласно

 График данной зависимости П = П(h) — прямая линия, проходящая через начало координат

(рис. 15), угол наклона которой к оси h тем больше, чем больше масса тела (так как tg=mg).