Ответы на вопросы к 2 коллоквиуму

Молекулярно-кинетическая теория — это раздел физики, изучающий свойства различных состояний вещества, основывающийся на представлениях о существовании молекул и атомов как мельчайших частиц вещества. В основе МКТ лежат три основных положения:           1. Все вещества состоят из мельчайших частиц: молекул, атомов или ионов.           2. Эти частицы находятся в непрерывном хаотическом движении, скорость которого определяет температуру вещества.           3. Между частицами существуют силы притяжения и отталкивания, характер которых зависит от расстояния между ними.           Основные положения МКТ подтверждаются многими опытными фактами. Существование молекул, атомов и ионов доказано экспериментально, молекулы достаточно изучены и даже сфотографированы с помощью электронных микроскопов. Способность газов неограниченно расширяться и занимать весь предоставленный им объем объясняется непрерывным хаотическим движением молекул. Упругость газов, твердых и жидких тел, способность жидкостей смачивать некоторые твердые тела, процессы окрашивания, склеивания, сохранения формы твердыми телами и многое другое говорят о существовании сил притяжения и отталкивания между молекулами. Явление диффузии — способность молекул одного вещества проникать в промежутки между молекулами другого — тоже подтверждает основные положения МКТ. Явлением диффузии объясняется, например, распространение запахов, смешивание разнородных жидкостей, процесс растворения твердых тел в жидкостях, сварка металлов путем их расплавления или путем давления. Подтверждением непрерывного хаотического движения молекул является также и броуновское движение — непрерывное хаотическое движение микроскопических частиц, нерастворимых в жидкости.           Движение броуновских частиц объясняется хаотическим движением частиц жидкости, которые сталкиваются с микроскопическими частицами и приводят их в движение. Опытным путем было доказано, что скорость броуновских частиц зависит от температуры жидкости. Теорию броуновского движения разработал А. Эйнштейн. Законы движения частиц носят статистический, вероятностный характер. Известен только один способ уменьшения интенсивности броуновского движения — уменьшение температуры. Существование броуновского движения убедительно подтверждает движение молекул.           Любое вещество состоит из частиц, поэтому количество вещества v принято считать пропорциональным числу частиц, т. е. структурных элементов, содержащихся в теле.           Единицей количества вещества является моль. Моль — это количество вещества, содержащее столько же структурных элементов любого вещества, сколько содержится атомов в 12 г углерода С12. Отношение числа молекул вещества к количеству вещества называют постоянной Авогадро:                      Постоянная Авогадро показывает, сколько атомов и молекул содержится в одном моле вещества. Молярная масса — масса одного моля вещества, равная отношению массы вещества к количеству вещества:           М = m/v.           Молярная масса выражается в кг/моль. Зная молярную массу, можно вычислить массу одной молекулы:                      Средняя масса молекул обычно определяется химическими методами, постоянная Авогадро с высокой точностью определена несколькими физическими методами. Массы молекул и атомов со значительной степенью точности определяются с помощью масс-спектрографа.           Массы молекул очень малы. Например, масса молекулы воды:            Молярная масса связана с относительной молекулярной массой Мг. Относительная молекулярная масса — это величина, равная отношению массы молекулы данного вещества к 1/12 массы атома углерода С12. Если известна химическая формула вещества, то с помощью таблицы Менделеева может быть определена его относительная масса, которая, будучи выражена в килограммах, показывает величину молярной массы этого вещества.           Диаметром молекулы принято считать минимальное расстояние, на которое им позволяют сблизиться силы отталкивания. Однако понятие размера молекулы является условным. Средний размер молекул порядка 10^-10м.           2.     С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров - давление, объем или температура - остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами.    Процессы, протекающие при неизменном значении одного из параметров, называютизопроцессами (от греческого слова «изос» - равный). Правда, в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объема. Лишь в лабораторных условиях удается поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс - это идеализированная модель реального процесса, которая только приближенно отражает действительность.    Изотермический процесс. Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называютизотермическим. Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой - термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.    Согласно уравнению состояния идеального газа (10.4) в любом состоянии с неизменной температурой произведение давления газа на его объем остается постоянным:

   Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.    Этот закон экспериментально был открыт английским ученым Р. Бойлем (1627-1691) и несколько позже французским ученым Э. Мариоттом (1620-1684). Поэтому он носит названиезакона Бойля - Мариотта.    Закон Бойля - Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха. Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.    Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют изотермой. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой (рис.10.1).

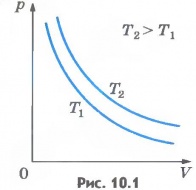
   Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если V=const. Поэтому изотерма, соответствующая более высокой температуре T₂, лежит выше изотермы, соответствующей более низкой температуре T₁(см. рис.10.1).    Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость молекул после ударов о поршень увеличивается, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.    Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всем сосуде. Если значения давления и температуры в различных точках объема разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние. Равновесное состояние - это состояние, при котором температура и давление во всех точках объема одинаковы. Параметры состояния газа могут быть определены, если он находится в равновесном состоянии. Процесс, при котором все промежуточные состояния газа являются равновесными, называют равновесным процессом. Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.    Изобарный процесс. Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (от греческого слова «барос» - вес).    Согласно уравнению (10.4) в любом состоянии газа с неизменным давлением отношение объема газа к его температуре остается постоянным: 

   Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.    Этот закон был установлен экспериментально в 1802 г. французским ученым Ж. Гей-Люссаком (1778-1850) и носит название закона Гей-Люссака. Согласно уравнению (10.7) объем газа при постоянном давлении пропорционален температуре:

   Эта зависимость графически изображается прямой, которая называется изобарой(рис.10.2). Разным давлениям  соответствуют  разные  изобары. С ростом давления объем газа при постоянной температуре согласно закону Бойля - Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению p₂, лежит ниже изобары, соответствующей более низкому давлению p₁.

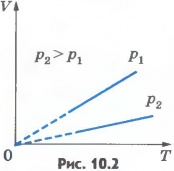
   В области низких температур все изобары идеального газа сходятся в точке T=0. Но это не означает, что объем реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (10.4) неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может.    Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем, если внешнее давление постоянно. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.    Изохорный процесс. Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным (от греческого слова «хорема» - вместимость).    Из уравнения состояния (10.4) вытекает, что в любом состоянии газа с неизменным объемом отношение давления газа к его температуре остается постоянным: 

   Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.    Этот газовый закон был установлен в 1787 г. французским физиком Ж.Шарлем (1746-1823) и носит название закона Шарля. Согласно уравнению (10.9) давление газа при постоянном объеме пропорционально температуре:

   Эта зависимость изображается прямой, называемой изохорой (рис.10.3). Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля - Мариотта падает. Поэтому изохора, соответствующая большему объему V₂, лежит ниже изохоры, соответствующей меньшему объему V₁.

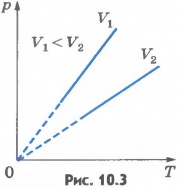
1.    В соответствии с уравнением (10.10) все изохоры идеального газа начинаются в точкеT=0. Значит, давление идеального газа при абсолютном нуле равно нулю.    Увеличение давления газа в любом сосуде или в электрической лампочке при нагревании можно считать изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объема.    Газовые законы - частный случай уравнения состояния идеального газа, один из параметров которого остается постоянным.

 Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона ) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

• p — давление,

• V_μ — молярный объём,

• T — абсолютная температура,

• R — универсальная газовая постоянная.

Так как  , где где ν — количество вещества, а   , где m — масса, μ — молярная масса, уравнение состояния можно записать:

      Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

Уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — закон Гей-Люссака.

— закон Шарля

3. Идеальный газ. Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. В модели идеального газа предполагается следующее: молекулы обладают пренебрежимо малым объемом по сравнению с объемом сосуда, между молекулами не действуют силы притяжения, при соударениях молекул друг с другом и со стенками сосуда действуют силы отталкивания.

Давление идеального газа. Одним из первых и важных успехов молекулярно-кинетической теории было качественное и количественное объяснение явления давления газа на стенки сосуда.

   Качественное объяснение давления газа заключается в том, что молекулы идеального газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела. При столкновении молекулы со стенкой сосуда проекция   вектора скорости на ось ОХ, перпендикулярную стенке, изменяет свой знак на противоположный, но остается постоянной по модулю (рис. 82).

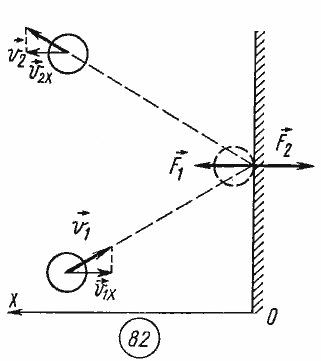
Поэтому в результате столкновения молекулы со стенкой проекция ее импульса на ось ОХ изменяется от   до  . Изменение импульса молекулы показывает, что на нее при столкновении действует сила  , направленная от стенки. Изменение импульса молекулы равно импульсу силы  :

 .

Во время столкновения молекула действует на стенку с силой  , равной по третьему закону Ньютона силе   по модулю и направленной противоположно. 

   Молекул газа очень много, и удары их о стенку следуют один за другим с очень большой частотой. Среднее значение геометрической суммы сил, действующих со стороны отдельных молекул при их столкновениях со стенкой сосуда, и является силой давления газа. Давление газа равно отношению модуля силы давления   к площади стенки S:

.

На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяло вычислить давление газа, если известны масса m₀ молекулы газа, среднее значение квадрата скорости молекул   и концентрацияn молекул:

 . (24.1)

Уравнение (24.1) называют основным уравнением молекулярно-кинетической теории.    Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа  :

,

получим

 . (24.2)

Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

4. Если газ находится в равновесии, молекулы движутся хаотически, и все направления их движения равновероятны. Скорости молекул могут быть самыми различными по модулю и при каждом соударении с другими молекулами изменяются случайным образом.

В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был выведен теоретически Дж. Максвеллом. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по модулям скоростей. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), скорости которых заключены в этом интервале.

Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, то есть:

dN(v)/N=f(v)dv, откуда f(v)=dN(v)/Ndv (28)

Применяя методы теории вероятностей, Дж. Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения:

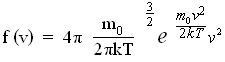 (29)

Из (29) следует, что конкретное распределение зависит от рода газа (от массы молекулы ) и от его термодинамической температуры. Очевидно, что функция распределения не зависит ни от давления, ни от объема газа. График функции распределения имеет вид, показанный на рис. 5.

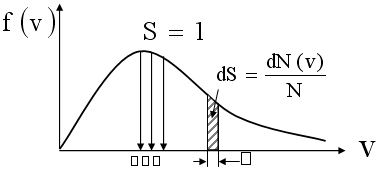  Рис. 5. График функции распределения молекул по скоростям

Выражение dN(v)/N=f(v)dv представляет собой вероятность встретить молекулу со скоростью, принадлежащей интервалу (v;v+dv). Эта вероятность равна площади заштрихованной полоски с основанием dv (рис. 5). Относительная доля молекул, имеющих определенную скорость, равна нулю.

Площадь под кривой f(v) равна вероятности достоверного события – встретить молекулу со скоростью, принадлежащей интервалу (0;∞), то есть равна единице. Это означает, что функция удовлетворяет условию нормировки:

f(v)dv=1 (30)

Наиболее вероятная v_в, средняя арифметическая <v> и среднеквадратичная скорости <v_кв> молекул.

Наиболее вероятная скорость соответствует максимуму функции распределения, ведь именно этой скоростью будет обладать наибольшее число молекул. Ее значение найдется из условия экстремума функции f(v):

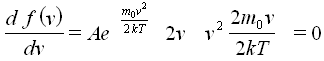
v_в=√(2kT/m₀)=√(2kN_AT/m₀N_A)=√(2RT/M) (31)

Отсюда видно, что при увеличении температуры T максимум кривой распределения сместится вправо, так как при увеличении T увеличивается v_в, которая определяет положение максимума. Но площадь под кривой должна оставаться постоянной. Поэтому величина максимума будет уменьшаться. Влияние же массы молекулы m₀ будет обратным. Влияние температуры и массы молекулы на вид функции распределения показано на рис. 6.

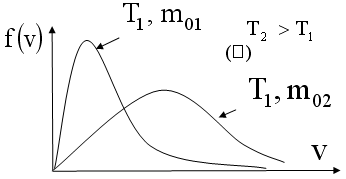  Рис. 6. Влияние параметров газа на вид функции распределения

Выражение для средней скорости <v> определяется по формуле:

<v>= vf(v)dv=√(8kT/πm₀)=√(8kN_AT/πm₀N_A)=√(8RT/πM) (32)

Аналогично найдем выражение для среднеквадратичной скорости:

<v_кв>= v²f(v)dv.

Произведя интегрирование, получим:

<v_кв>=√(3RT/M) (33)

Из сравнения найденных скоростей вытекает:

<v_кв>=√(3RT/M) > <v>=√(8RT/πM) > v_в=√(2RT/M).

Соотношения между скоростями:

v_в : <v> : <v_кв> = √2 : √(8/π) : √3 = 1 : 1,13 : 1,22

При комнатной температуре T=300K средняя арифметическая скорость молекул кислорода будет равна:

<v>=√(8RT/πM)=√(8·8,31·300/π·0,032)≈500 м/с

Первое экспериментальное определение скоростей молекул было осуществлено Штерном в 1920 г: подтвердилась правильность оценки средней скорости молекул, вытекающей из распределения Максвелла; о характере распределения этот опыт дал лишь приближенные сведения. Более точно закон Максвелла был проверен в опыте Ламмерта (1929 г.).

Из функции распределения молекул по модулям скоростей можно получить функцию распределения молекул по кинетическим энергиям теплового движения:

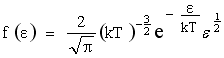 (34)

Найдем среднюю кинетическую энергию <ε> молекулы идеального газа:

 

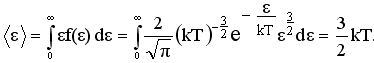
5. Барометрическая формула. Распределение Больцмана. Закон равномерного распределения энергии по степеням свободы.

Барометрическая формула:

,

где p — давление газа в слое, расположенном на высоте h,  p₀ — давление на нулевом уровне h = h₀,  M — молярная масса газа,  R — газовая постоянная,  T — абсолютная температура.

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

Где:  n — концентрация молекул на высоте h,  n₀ — концентрация молекул на начальном уровне h = 0,  m — масса частиц,  g — ускорение свободного падения,  k — постоянная Больцмана,  T — температура.

В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободымолекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная   , а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы:

,

где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы:i = i_пост. + i_вращ. + 2i_колеб.

Закон равнораспределения показывает, что при тепловом равновесии, любая степень свободы (компоненты векторов положения или скорость частицы), которая появляется только как квадратичная функция в энергии, обладает средней энергией равной ½k в T и поэтому вносит вклад ½k в теплоёмкость системы.

6. Средние скорости молекул, газа очень велики - порядка сотен метров в секунду при обычных условиях. Однако процесс выравнивая неоднородности в газе вследствие молекулярного движения протекает весьма медленно. Это объясняется тем, что молекулы при перемещении испытывают соударения с другими молекулами. При каждом соударении скорость молекулы изменяется по величине и направлению. Вследствие этого, скорость, с которой молекула диффундирует из одной части газа в другую, значительно меньше средней скорости молекулярного движения. Для оценки скорости движения молекул вводится понятие средней длины свободного пробега. Таким образом, средняя дли свободного пробега   - это среднее расстояние, которое проходит молекула от столкновения до столкновения.Для определения   вычислим сначала среднее число соударений   выбранной молекулы с другими молекулами за единицу времени. Будем считать, что молекула после соударения продолжает двигаться по прямой со средней скоростью движения   .

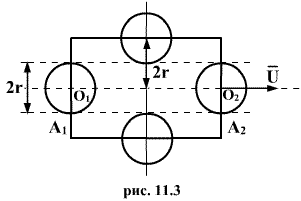
Молекулы, с которыми соударяется выбранная молекула, в первом приближении считаем неподвижными и принимаем их за сферические тела радиуса r. Пусть выбранная молекула движется вправо из положения   в положение   по прямой   (рис.11.3). При своем движении она испытывает соударения с теми неподвижными молекулами, центры которых лежат не дальше чем 2r от траектории   . Иными словами, движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной   , т.е.

.

Если концентрация молекул n , то внутри рассмотренного цилиндра находится число молекул, равное

Это число   и определяет среднее число соударений за единицу времени.

Предположение о том, что все молекулы, кроме одной, неподвижны, является, конечно не верным. В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости. Поэтому вместо среднеарифметической скорости   должны входить средняя относительная скорость молекул   . Если скорости молекул распределены по закону Максвелла, то, как можно показать, средняя относительная скорость двух молекул однородного газа в   раз превышает   . Таким образом, среднее число соударений должно быть увеличено в   раз

(11.7)

Средний путь, проходимый молекулой за единицу времени, численно равен   . Поэтому средняя длина свободного пробега равна   или

(11.8)

Таким образом, средняя длина свободного пробега   не зависит от температуры газа, т.к. с ростом температуры одновременно возрастают и   , и   . При подсчете числа соударений и средней длины свободного пробега молекул за модель молекулы было принято шарообразное упругое тело. В действительности каждая молекула представляет собой сложную систему элементарных частиц и при рассмотрении упругого соударения молекул имелось в виду, что центры молекул могут сблизиться до некоторого наименьшего расстояния. Затем возникает силы отталкивания которые вызывают взаимодействие, подобное взаимодействию при упругом ударе. Среднее расстояние между центрами молекул, взаимодействующих, как при упругом ударе, называют эффективным диаметром   . Тогда

Явления переноса. Диффузия, вязкость, теплопроводность. Коэффициенты диффузии, вязкости, теплопроводности.

Явления переноса в термодинамически неравновесных системах      В термодинамически неравновесных системах возникают особые необратимые процес­сы, называемые явлениями переноса, в результате которых происходит пространствен­ный перенос энергии, массы, импульса. К явлениям переноса относятся теплопровод­ность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса).Для простоты ограничимся одномер­ными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориен­тирована в направлении переноса.      1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных сто­лкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье: 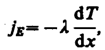(48.1)      где jE  — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х, l —теплопроводность,    — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE  и   – противоположны). Теплопроводность l численно равна плотности теплового потока при градиенте температуры, равном единице.  Можно показать, что (48.2) где сV— удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме), r — плотность газа, <v> — средняя скорость теплового движения молекул, <l> — средняя длина сво­бодного пробега.      2. Диффузия. Явление диффузии заключается в том, что происходит самопроиз­вольное проникновение и перемешивание частиц двух соприкасающихся газов, жид­костей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте. Явление диффузии для химически однородного газа подчиняется закону Фука: (48.3)      где jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), dr/dx — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки jm и dr/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинети­ческой теории газов, (48.4)      Коэффициент  диффузии в жидкости увеличивается с температурой, что обусловлено «разрыхлением» структуры жидкости при нагреве и соответствующим увеличением числа перескоков в единицу времени.      В твёрдом теле могут действовать несколько механизмов диффузии: обмен местами атомов с вакансиями(незанятыми узлами кристаллической решётки), перемещение атомов по междоузлиям, одновременное циклическое перемещение нескольких атомов, прямой обмен местами двух соседних атомов и т.д. Первый механизм преобладает, например, при образовании твёрдых растворов замещения, второй — твёрдых растворов внедрения.      Коэффициент диффузии в твёрдых телах крайне чувствителен к дефектам кристаллической решётки, возникшим при нагреве, напряжениях, деформациях и др. воздействиях. Увеличение числа дефектов (главном образом вакансий) облегчает перемещение атомов в твёрдом теле и приводит к росту коэффициента диффузии. Для коэффициента диффузии в твёрдых телах характерна резкая (экспоненциальная) зависимость от температуры. Так, коэффициент диффузии цинка в медь при повышении температуры от 20 до 300°С возрастает в 1014 раз.       3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона: 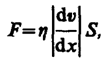(48.5)      где h — динамическая вязкость (вязкость), dv/dx — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S — площадь, на которую действует сила F.       Взаимодействие двух слоев согласно второму закону Ньютона можно рассматри­вать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно пред­ставить в виде 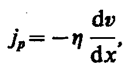(48.6)      где jp — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х,    — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и   противоположны).      Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле (48.7)      Из сопоставления формул (48.1), (48.3) и (48.6), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были установлены задолго до того, как они были обоснованы и выведены из молекулярно-кинетической теории, позволившей установить, что внешнее сходство их математи­ческих выражений обусловлено общностью лежащего в основе явлений теплопровод­ности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.      Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетического смысла коэффициентов l, D иh. Выражения для коэффициентов переноса выводятся из кинетической теории. Они записаны без вывода, так как строгое рассмот­рение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (48.2), (48.4) и (48.7) связывают коэффициенты переноса и характеристики теплового движения молекул. Из этих формул вытекают простые зависимости между l, D иh: 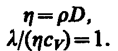Используя эти формулы, можно по найденным из опыта одним величинам определить другие.

Вязкость.

Вязкость - сопротивление, оказываемое телом движению отдельной его части без нарушения связи целого. Такое движение составляет характеристику жидкостей, как "капельных", так и "упругих", т. е. газов.      Внутреннее трение жидкостей возникает при движении жидкости из-за переноса импульса в направлении, перпендикулярном к направлению движения. Перенос импульса из одного слоя в другой осуществляется при скачках молекул, о которых говорилось выше.  Очевидно, что жидкость будет тем менее вязкой, чем меньше время t между скачками молекул, и значит, чем чаще происходят скачки. 

7. Важной характеристикой термодинамической системы является ее внутренняя энергия. Как известно, энергия тела состоит из кинетической энергии движения тела со скоростью v и потенциальной энергии тела во внешних силовых полях (гравитационном, магнитном и т. д.): 

E_мех=(1/2)·mv²+E_пот.

Согласно МКТ, все тела состоят из молекул, которые находятся в состоянии непрерывного, хаотического движения, то есть обладают кинетической энергией, а вследствие взаимодействия между собой обладают потенциальной энергией взаимодействия.  Внутренняя энергия – суммарная энергия хаотического (теплового) движения микрочастиц системы и энергия взаимодействия этих частиц.  Внутренняя энергия - однозначная функция термодинамического состояния системы (при переходе системы из одного состояния в другое изменение внутренней энергии определяется разностью значений внутренней энергии этих состояний и не зависит от пути перехода).  Как известно из механики, движение тел (или материальных точек) происходит в пространстве и во времени. Любое движение тела можно представить как комбинацию поступательного и вращательного движений. Положение тела в каждый момент времени характеризуется числом степеней свободы.  Число степеней свободы молекулы – число независимых переменных (координат), полностью определяющих положение системы в пространстве.  Молекулу одноатомного газа (в виду ее малости) можно рассматривать как материальную точку, которой приписывают три степени свободы поступательного движения: i=i_пост (рис. 8). 

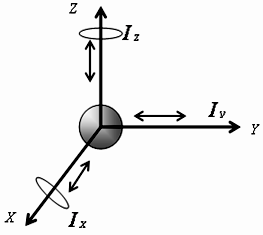  Рис. 8. К определению числа степеней свободы для одноатомной молекулы

Средняя кинетическая энергия поступательного движения одноатомной молекулы идеального газа равна: 

E₀=m₀{v_кв}²/2=3kT/2.

Вращательные степени свободы в данном случае не учитываются, так как момент инерции данной молекулы относительно каждой из осей: I_x=mr², I_y=mr², I_z=mr², расстояние до осей вращения r→0, следовательно I_x→0, I_y→0, I_z→0, тогда кинетическая энергия вращения для каждой из осей: 

E_к.вр.=Iω²→0.

Молекула двухатомного газа рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью (рис. 9). Кроме трех поступательных степеней свободы, у такой молекулы появляются две вращательные степени свободы: 

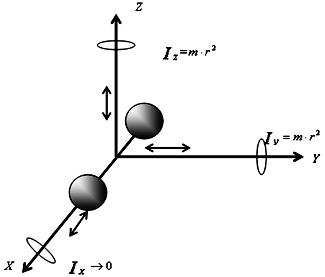  Рис. 9. К определению числа степеней свободы для двухатомной молекулы

i=i_пост+i_вращ=5

Трехатомная и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных (рис. 10): 

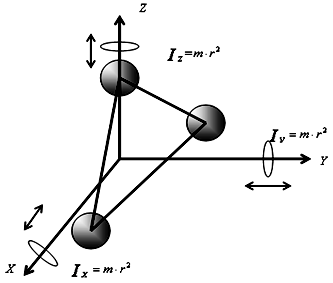  Рис. 10. К определению количества степеней свободы для трехатомной молекулы

i=i_пост+i_вращ=6

На самом деле, жесткой связи между атомами не существует. Атомы в молекуле могут сближаться и расходиться, то есть могут совершать колебания около положения равновесия. Энергия колебательного движения молекулы является суммой кинетической и потенциальной энергий, средние значения которых одинаковы. Таким образом, для реальных молекул необходимо учитывать также степени свободы колебательного движения.  В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы – в среднем энергия, равная . Средняя энергия молекулы равна: 

{ε}=[i/2]·kT, (46)

где i=i_пост+i_вращ+2i_колеб  Установлено, что однако энергия поступательного и вращательного движений молекулы значительно меньше энергии колебательного движения атомов в молекуле, поэтому колебательные степени свободы возбуждаются при высоких температурах.  Внутренняя энергия идеального газа складывается только из кинетических энергий всех молекул в данном объеме, так как потенциальной энергией взаимодействия молекул, согласно допущениям модели идеального газа (п.1.3), можно пренебречь.  Для одного моля идеального газа: 

U_m=EN_A=[i/2]·kN_AT

Внутренняя энергия для произвольной массы идеального газа: 

U=U_mυ=[i/2]·mRT/M

8. Внутренняя энергия — это энергия движения и взаимодействия частиц, из которых состоит тело. Внутренняя энергия зависит от температуры тела, его агрегатного состояния, от химических, атомных и ядерных реакций. Она не зависит ни от механического движения тела, ни от положения этого тела относительно других тел. Внутреннюю энергию можно изменить путем совершения работы и теплопередачи. Если над телом совершается работа, то внутренняя энергия тела увеличивается; если же это тело совершает работу, то его внутренняя энергия уменьшается. т. е. чтобы изменить внутреннюю энергию тела, нужно изменить его температуру. Увеличение внутренней энергии можно понаблюдать на интересном опыте «Воздушное огниво» . В прозрачный цилиндр с толстыми стенками из оргстекла помещают маленький кусочек ваты. Вдвигают в цилиндр поршень и резким движением опускают его вниз. За счёт совершенной работы внутренняя энергия воздуха при сжатии возрастает, увеличивается его температура, в результате чего вата воспламеняется.

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.

Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца[1]. Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника. Формулировка

Существует несколько эквивалентных формулировок первого начала термодинамики

В любой изолированной системе запас энергии остаётся постоянным.[2] Это — формулировка Дж. П. Джоуля (1842 г.).

Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил

Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.

\oint dU = 0

Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале \mu, и работы A'[3], совершённой над системой внешними силами и полями, за вычетом работы A, совершённой самой системой против внешних сил

\Delta U = Q - A + \mu\Delta N + A'.

Для элементарного количества теплоты \delta Q, элементарной работы \delta A и малого приращения dU внутренней энергии первый закон термодинамики имеет вид:

dU=\delta Q-\delta A+\mu dN+\delta A'.

Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.

Важно заметить, что dU и dN являются полными дифференциалами, а \delta A и \delta Q — нет.

Частные случаи

Рассмотрим несколько частных случаев:

Если \delta Q > 0, то это означает, что тепло к системе подводится.

Если \delta Q < 0, аналогично — тепло отводится.

Если \delta Q = 0, то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.

Обобщая: в конечном процессе 1 \to 2 элементарные количества теплоты могут быть любого знака. Общее количество теплоты, которое мы назвали просто Q — это алгебраическая сумма количеств теплоты, сообщаемых на всех участках этого процесса. В ходе процесса теплота может поступать в систему или уходить из неё разными способами.

При отсутствии работы над системой и потоков энергии-вещества, когда \delta A'=0, \delta Q=0, dN=0, выполнение системой работы \delta A приводит к тому, что \Delta U<0, и энергия системы U убывает. Поскольку запас внутренней энергии U ограничен, то процесс, в котором система бесконечно долгое время выполняет работу без подвода энергии извне, невозможен, что запрещает существование вечных двигателей первого рода.

Первое начало термодинамики:

при изобарном процессе

Q = \Delta U + A = \Delta U + p\Delta V

при изохорном процессе (A=0)

Q = \Delta U = {m\over M} C_V\Delta T

при изотермическом процессе (\Delta U=0)

Q = A = {m\over M} R T \ln{V_2\over V_1}

Здесь \ m — масса газа, \ M — молярная масса газа, \ C_V — молярная теплоёмкость при постоянном объёме, \ p, V, T — давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.

9. Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT[1]:

C = {\delta Q \over \delta T}.

Единица измерения теплоёмкости в Международной системе единиц (СИ) — Дж/К.

Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.

Массовая теплоёмкость (С), также называемая просто удельной теплоёмкостью — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг−1·К−1).

Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м−3·К−1).

Молярная теплоёмкость (Сμ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)).

Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).

Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна:

c_v = \frac{i}{2}R,

где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная.

А при постоянном давлении

c_p = c_v + R = \frac{i+2}{2} R.

Переход вещества из одного агрегатного состояния в другое сопровождается скачкообразным изменением теплоёмкости в конкретной для каждого вещества температурной точке превращения — температура плавления (переход твёрдого тела в жидкость), температура кипения (переход жидкости в газ) и, соответственно, температуры обратных превращений: замерзания и конденсации.

Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К).

Cp = Cv + R

Оно показывает, что расширение моля идеального газа при постоянном давлении и изменении его температуры на 1 Кельвин требует дополнительного, по сравнению с изобарическим расширением, количества теплоты, необходимого для совершения работы. Это значение равно универсальной газовой постоянной....;)

10.

Ответы на вопросы к 1 коллоквиуму

1.

Механическое движение — изменение пространственного положения тела относительно других тел с течением времени Материальная точка — тело, обладающее массой, размерами которого можно в данной задаче пренебречь.

Система отсчета — совокупность тела отсчета, связанной с ним системы координат и часов Траектория — воображаемая линия, соединяющая положения материальной точки в ближайшие последовательные моменты времени

Радиус-вектор — вектор, соединяющий начало отсчета с положением материальной точки в произвольный момент времени Закон движения — зависимость радиуса-вектора или координат от времени.

Перемещение — вектор, проведенный из начального положения материальной точки в конечное Путь — длина участка траектории, пройденного материальной точкой за данный промежуток времени Средняя скорость — скалярная величина, равная отношению пройденного пути к промежутку времени, в течение которого этот путь пройден.

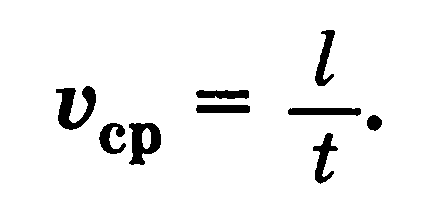
Скорость — векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, в течение которого это перемещение произошло.

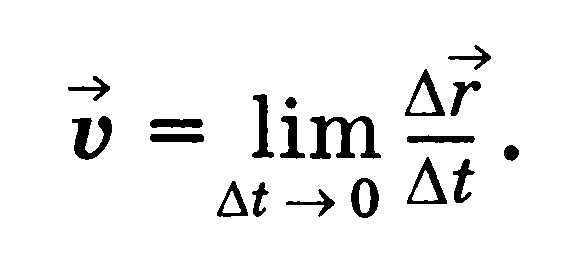
Единица скорости — метр в секунду (м/с).

Скорость тела направлена по касательной к траектории в сторону движения тела

Относительная скорость первого тела относительно второго равна разности векторов скорости тел

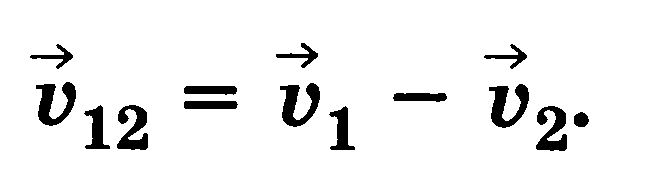
Равномерное прямолинейное движение — движение с постоянной по модулю и направлению скоростью.

Закон равномерного прямолинейного движения по оси X

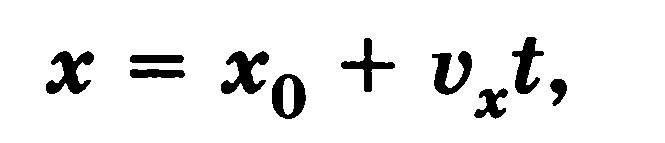
где х₀ — начальная координата тела, v_x — проекция скорости тела на ось X

Ускорение — векторная физическая величина, равная пределу отношения изменения скорости тела к промежутку времени, в течение которого это изменение произошло.

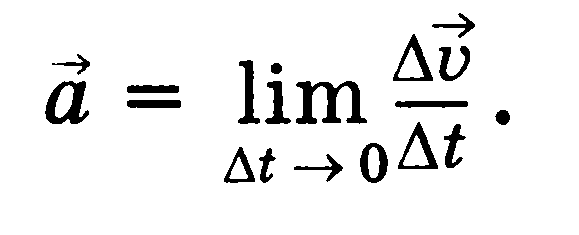
Единица ускорения — метр на секунду в квадрате (м/с²) Равноускоренное прямолинейное движение — прямолинейное движение, при котором ускорение параллельно скорости и постоянно по модулю.

Равнозамедленное прямолинейное движение — прямолинейное движение, при котором ускорение антипараллельно (противоположно направлено) скорости и постоянно по модулю

Равнопеременное движение —

движение с постоянным по модулю и направлению ускорением Закон равнопеременного движения

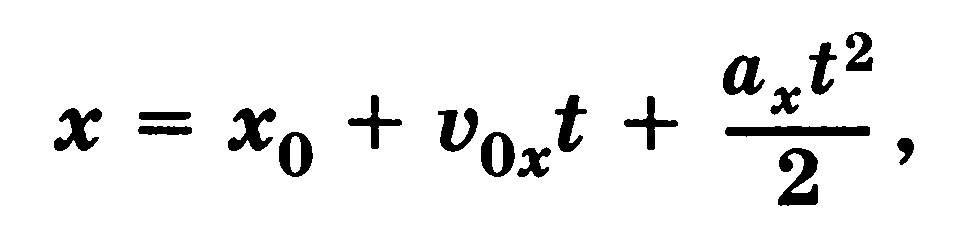
где v_0x и а_х — проекции начальной скорости и ускорения тела на ось X. Проекция скорости на ось X при равнопеременном движении линейно зависит от времени

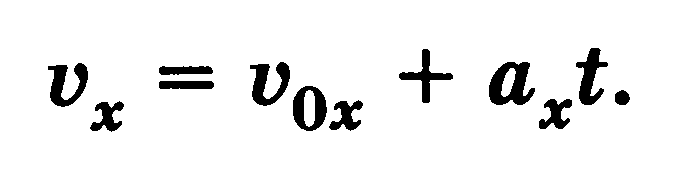
В отсутствие сил сопротивления воздуха все тела независимо от их массы падают на Землю с одинаковым ускорением свободного падения (g = 9,8 м/с²)

Криволинейное баллистическое движение — результат сложения двух прямолинейных движений равномерного движения по горизонтальной оси и равнопеременного движения по вертикальной оси Баллистической кривой в отсутствие сопротивления воздуха является парабола

Максимальная дальность полета тела в поле тяжести (в отсутствие сопротивления воздуха) достигается при его вылете под углом 45° к горизонту

В верхней точке траектории вертикальная компонента скорости равна нулю

Периодическое движение — движение, повторяющееся через постоянный промежуток времени. Период — минимальный интервал времени, через который движение повторяется

Период вращения — время одного оборота по окружности Угловая скорость — физическая величина, равная отношению угла поворота к интервалу времени, в течение которого этот поворот произошел.

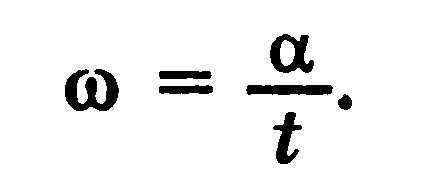
Единица угловой скорости — радиан в секунду (рад/с)

Угловая скорость связана с периодом вращения и частотой соотношениями

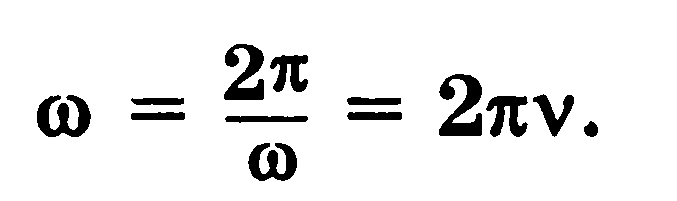
Линейная скорость движения тела по окружности радиусом r пропорциональна его угловой скорости

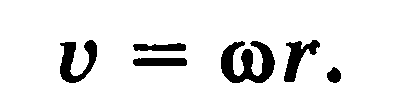
Касательное (тангенциальное) ускорение — составляющая ускорения тела, движущегося по криволинейной траектории, направленная по касательной Нормальное (центростремительное) ускорение — составляющая ускорения тела, движущегося по криволинейной траектории, направленная перпендикулярно траектории.

Модуль нормального ускорения тела при движении по окружности радиусом r

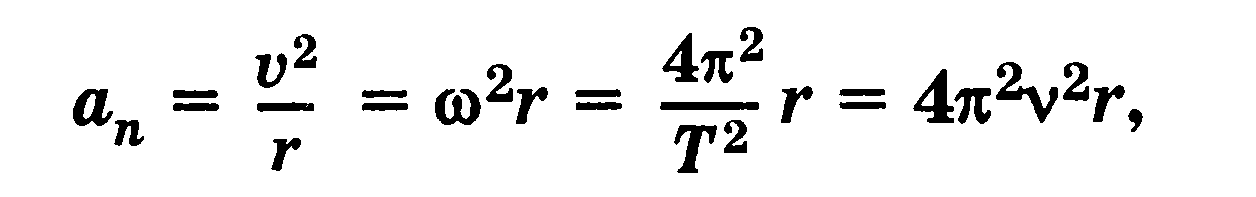
где v — скорость тела, со — угловая скорость, Т — период вращения, v — частота вращения Гармонические колебания — колебания, при которых физическая величина изменяется со временем синусоидально (или косинусоидально).

2.

Враща́тельное движе́ние — вид механического движения. При вращательном движении материальной точки она описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым.

Вращение характеризуется углом  , измеряющимся в градусах или радианах, угловой скоростью   (измеряется в рад/с) и угловым ускорением   (единица измерения — рад/с²).

При равномерном вращении (T - период вращения),

• Частота вращения — число оборотов в единицу времени.

,

• Период вращения — время одного полного оборота. Период вращения 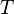  и его частота 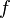  связаны соотношением  .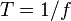

• Линейная скорость точки, находящейся на расстоянии R от оси вращения

,

• Угловая скорость вращения тела

.

Динамические характеристики

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные изуравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:

.

В этой формуле момент инерции играет роль массы, а угловая скорость - роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы  .

• Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всехn материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности впоступательном движении.

3.

Законы механики Ньютона

1) Первый закон Ньютона: Существуют такие системы отсчета, называемые инерциальными, относительно которых свободные тела движется равномерно и прямолинейно.

Первый закон механики, или закон инерции, как его часто называют, бал, по существу, установлен еще Галилеем, но общую формулировку ему дал Ньютон.

Свободным телом – называют тело, на которое не действуют какие – либо другие тела или поля. При решении некоторых задач тело можно считать свободным, если внешние воздействия уравновешены.

Системы отсчета, в которых свободная материальная точка покоится или движется прямолинейно и равномерно, называются инерциальными системами отсчета. Прямолинейное и равномерное движение свободной материальной точки в инерциальной системе отсчета называется движением по инерции.При таком движении вектор скорости материальной точки остается постоянным (  = const ). Покой точки является частным   случаем движения по  инерции (  =0).

В инерциальных системах отсчета покой или равномерное движение представляет собой естественное состояние, а динамика должна объяснить изменение этого состояния (т.е. появление уско­рения тела под действием сил). Свободных тел, не подверженных воздействию со стороны других тел не существует. Однако, благо­даря убыванию всех: известных взаимодействий с увеличением рас­стояния, такое тело можно реализовать с любой требуемой, точ­ностью.

Системы отсчета, в которых свободное тело не сохраняет ско­рость движения неизменной, называются неинерциальными. Неинерциальной является система отсчета, движущаяся с ускорением отно­сительно любой инерциальной системы отсчета. В неинерциальной системе отсчета даже свободное тело может двигаться с ускорением.

Равномерное и прямолинейное движение системы отсчета не влияет на ход механических явлений, протекающих в ней. Никакие механические опыты не позволяют отличить покой инерциальной системы отсчета от ее равномерного прямолинейного движения. Для любых механических явлений все инициальные системы отсче­та оказываются равноправными. Эти утверждения выражают меха­нический принцип относительности (принцип относительности Галилея). Принцип относительности является одним из наиболее об­щих законов природы, в специальной теории относительности он распространяется на электромагнитные и оптические явления.