Построение линейной модели множественной регрессии
Наконец, я построил линейную модель множественной регрессии. Были получены следующие результаты.
Рис. 14 – результаты оценивания параметров линейной модели множественной регрессии
Как видно из вероятности статистики теста Фишера (Prob(F-statistic)=0,000000), модель является значимой. Но если взглянуть на значимость зависимых величин (Prob.), мы увидим, что из них значима лишь одна – уровень национального дохода на душу населения. Тогда начнём по очереди удалять из модели незначимые величины, начиная с самой незначимой (в данном случае – с охвата среднего образования).
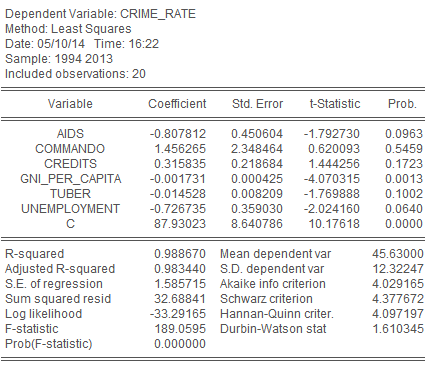
Рис. 15 – результаты оценивания параметров линейной модели множественной регрессии после удаления незначимой переменной school_enrollment
Как видим, в модели по-прежнему сохраняются незначимые переменные. Самая незначимая теперь, резко выделяющаяся на фоне остальных – это наличие/отсутствие коммандо. Удаляем из модели и её.
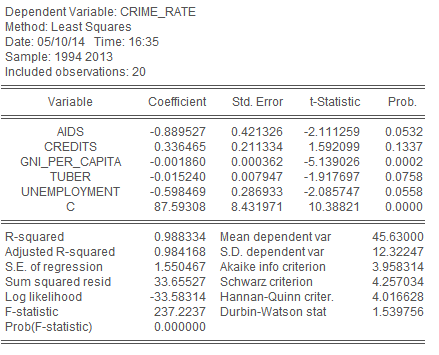
Рис. 16 - результаты оценивания параметров линейной модели множественной регрессии после удаления незначимой переменной commando
Картина значительно улучшилась – значимость переменных теперь куда ближе к необходимой. Однако все они, кроме одной (gni_per_capita), по-прежнему незначимы. Теперь удаляем самую незначимую переменную процентной ставки по кредитам.
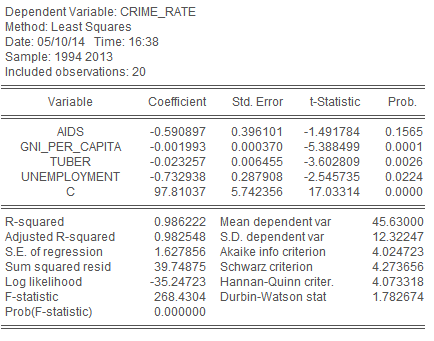
Рис. 17 - результаты оценивания параметров линейной модели множественной регрессии после удаления незначимой переменной credits
Теперь значимы все переменные, кроме одной – процента больных ВИЧ/СПИД. Для построения правильной модели необходимо удалить и её.
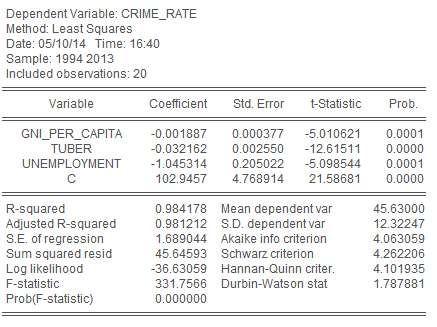
Рис. 18 - результаты оценивания параметров линейной модели множественной регрессии после удаления незначимой переменной aids
Вот теперь все переменные в линейной модели значимы (как и она сама). В итоге я получил модель, в которой переменная crime_rate (уровень убийств на 100 тыс. чел.) зависит от переменных gni_per_capita (уровень национального дохода на душу населения), tuber (уровень заболеваемости туберкулёзом на 100 тыс. чел.) и unemployment (уровень безработицы в процентах к трудоспособному населению). Теперь можно переходить к дальнейшему исследованию модели.
Гистограмма частот
Я посмотрел гистограмму частот каждой переменной. В результате были получены следующие гистограммы.
Уровень убийств.
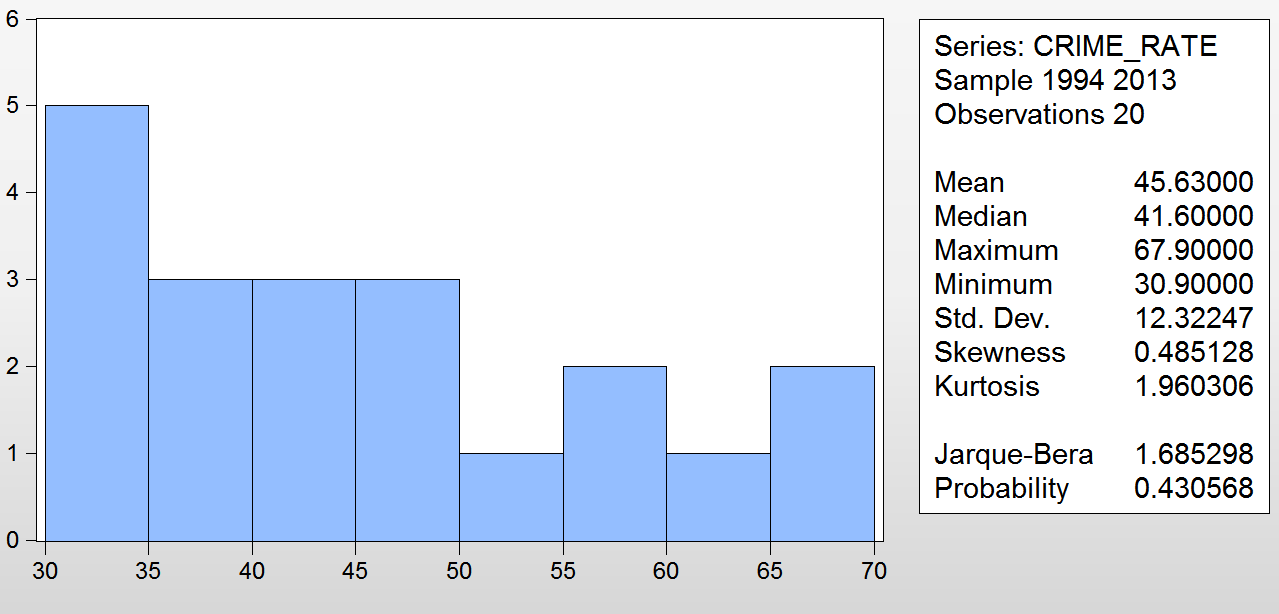
Рис. 19 – гистограмма уровня убийств на 100 тыс. чел. в 1994-2013 гг.
Уровень убийств распределён ненормально, как и его остатки по результатам теста Харке-Бера (скорее он ближе к Парето-распределению). Видно, что самая большая доля значений – от 30 до 35 (5 из 20). Ещё три группы значений (35-40, 40-45, 45-50) вместе насчитывают 9 наблюдений. Высокие же значения переменной относительно немногочисленны: три значения в диапазоне от 50 до 60 и столько же – от 60 до 70. Всё это говорит о небольшой доле крупных значений в выборке и значительной – малых и средних (среднее значение равно 45,6). Таким образом, уровень убийств был действительно высоким лишь в течение недолгого времени (3-6 лет), а в большую часть периода 1994-2013 гг. он был уже далеко не так высок и имел тенденцию к быстрому снижению (т.к. все группы с небольшими значениями достаточно велики по своей доле в выборке).
Национальный доход на душу населения.
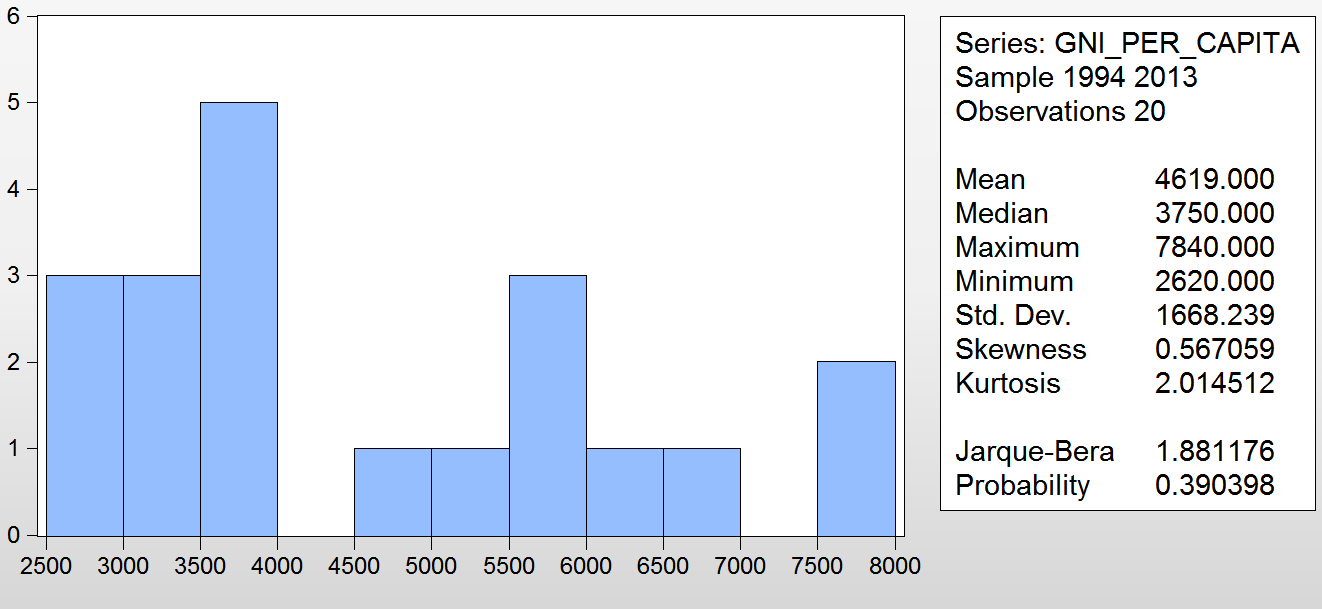
Рис. 20 – гистограмма национального дохода на душу населения в 1994-2013 гг.
Распределение этой переменной также далеко от нормального. Впрочем, оно мало похоже и на Парето-распределение. Есть два «провала» на шкале, в которые не попадает ни одно из значений переменной. Они ограничивают более-менее нормально распределённую середину шкалы. Крайние же значения, напротив, обладают большей частотой, чем хвосты середины. Если учитывать динамику НД, то такая гистограмма говорит о том, что показатели национального дохода на душу населения долгое время менялись довольно медленно и незначительно, а затем начали резко расти, порой «проскакивая» определённые интервалы значений. Три случая в диапазоне от 5500 до 6000 – это застойный период конца 2000-х гг. Два значения между 7500 и 8000 долларов на душу населения – это последние два года исследуемого периода, когда рост переменной замедлился. Таким образом, мы можем наблюдать пусть и медленный вначале и единожды прерывавшийся ближе к концу, но неуклонный рост национального дохода на душу населения в ЮАР.
Количество больных туберкулёзом.
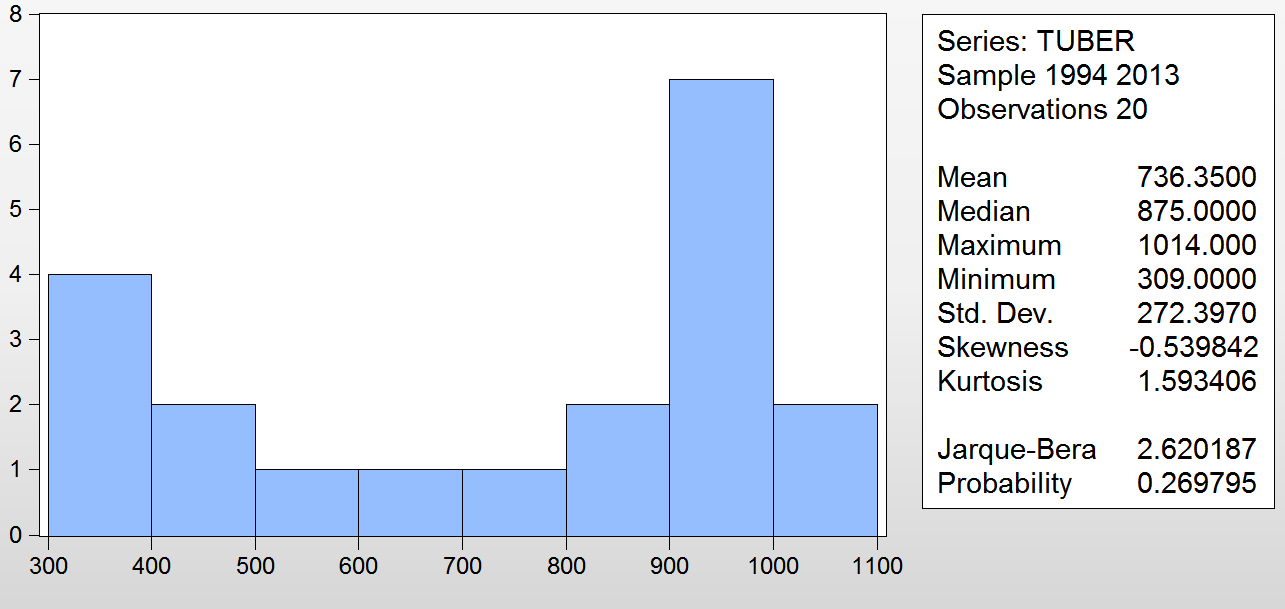
Рис. 21 – гистограмма количества больных туберкулёзом на 100 тыс. чел. населения в 1994-2013 гг.
Распределение данной переменной скорее похоже на обратное нормальному: наибольшие и наименьшие значения выборки имеют большую частоту, чем средние. Впрочем, даже с точки зрения такой модели частоты распределены неравномерно – резко выделяются самые маленькие значения (от 300 до 400 чел. на 100 тыс. населения) и одни из самых больших (от 900 до 1000). В сумме они составляют 11 случаев, т.е. больше половины выборки. Это отлично сочетается с данными графика, которые говорят о том, что эта непрерывно возрастающая функция имела самый слабый рост (а значит, самое большое количество близких друг к другу значений) в начале и в конце рассматриваемого периода. В другие же периоды она возрастала достаточно быстро, значения резко возрастали, и потому их частотность была невелика.
Уровень безработицы.
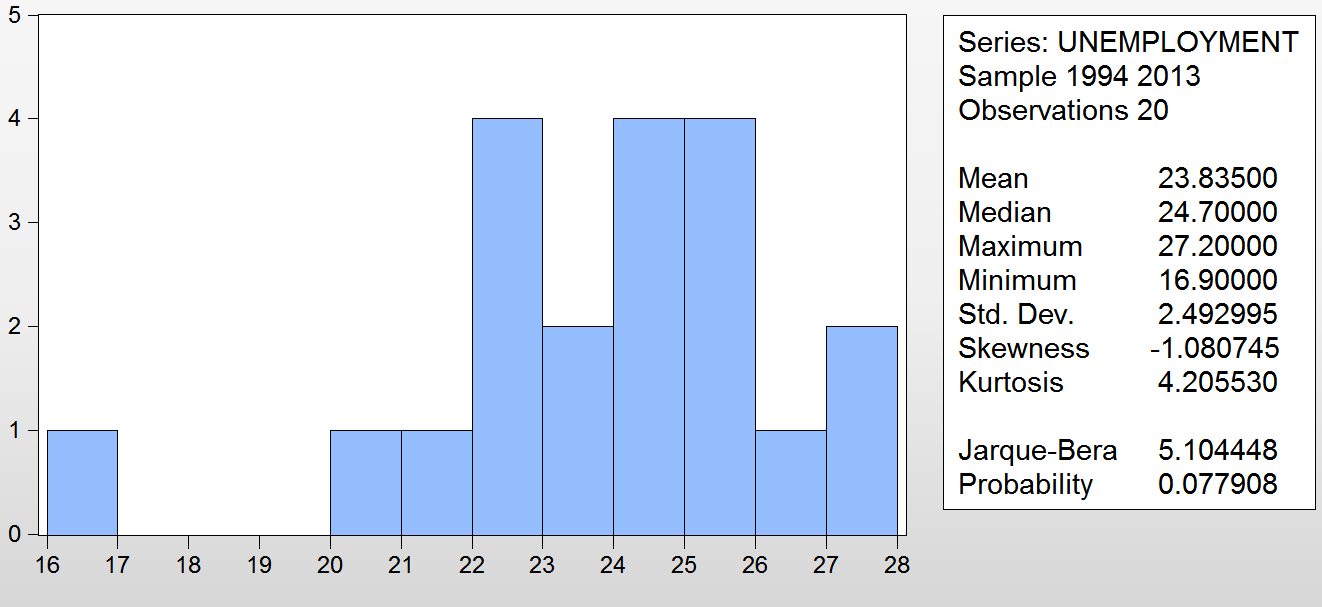
Рис. 22 – гистограмма уровня безработицы в 1994-2013 гг.
Тест Харке-Бера говорил о том, что остатки переменной уровня безработицы были распределены наиболее ненормально. Однако распределение самой переменной на фоне остальных выглядит очень близким к нормальному, если не считать значительного «провала» в районе среднего значения переменной и возрастания на крайнем справа отрезке от 27 до 28. Это говорит о том, что уровень безработицы большую часть периода 1994-2013 гг. был средним, а его крайние значения – редкими, т.е. не было ни постоянного роста, ни постоянного снижения безработицы (что подтверждается и графиком переменной).