3.2 Определение направления процесса по уравнению изотермы химической реакции

Изменение энергии Гиббса для химической реакции, записанной в виде (2.26) и протекающей в газовой фазе, при условиях, для которых применимы законы идеального газообразного состояния, можно вычислить по уравнению изотермы Вант – Гоффа

, (2.39)

где – начальные (неравновесные) парциальные давления реагирующих веществ.

Уравнение изотермы может быть записано также в следующем виде (при T, V = const):

, (2.40)

где – начальные (неравновесные) концентрации продуктов реакции и исходных веществ.

Уравнение изотермы можно представить в более компактном виде

, (2.41)

где

.

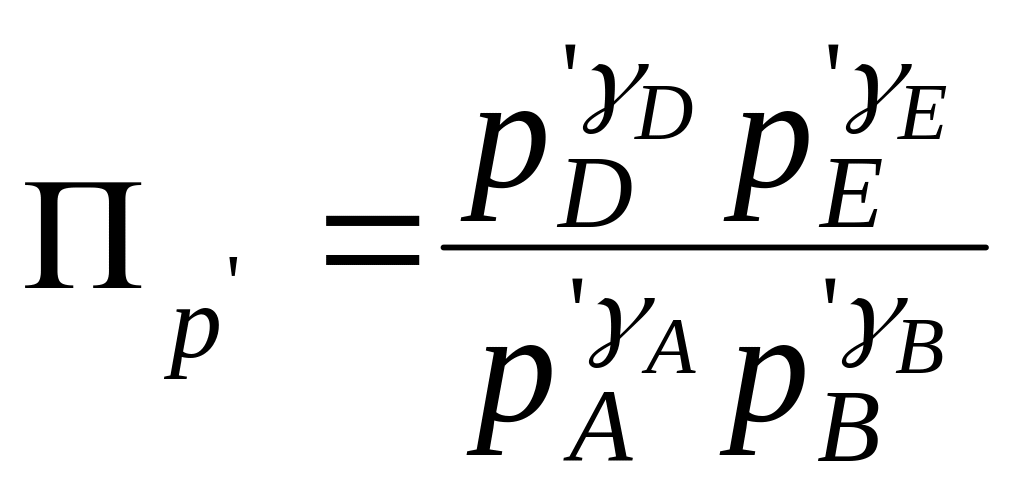По знаку и можно судить о возможности протекания данной реакции. Если согласно расчету <0 ( ), то реакция самопроизвольно пойдет в прямом направлении (слева направо). В случае, когда >0 ( ), процесс является необратимым несамопроизвольным, т. е. реакция будет протекать в обратном направлении. При =0 ( ) система находится в равновесии.

Приближенные данные о протекании реакции можно также получить по стандартному изменению энергии Гиббса, которая определяется по уравнению (2.25). Практически с достаточно большой вероятностью можно считать, что если кДж/моль, то реакция термодинамически возможна; если кДж/моль, то реакция термодинамически запрещена; если значение находится в интервале между этими двумя значениями, то нужно сделать точный расчет по полному уравнению изотермы (2.39).

3.3 Зависимость константы равновесия от температуры

Влияние температуры на константу равновесия выражается уравнением изобары (изохоры) Вант – Гоффа

; (2.42)

. (2.43)

Согласно уравнению (2.42) влияние температуры на константу равновесия обусловливается знаком теплового эффекта. Если , т. е. тепловой эффект реакции положителен (реакция эндотермическая), то температурный коэффициент константы равновесия также положителен: . Следовательно, для эндотермической реакции с повышением температуры константа равновесия будет увеличиваться, т.е. химическое равновесие будет смещаться в сторону продуктов реакции. При (экзотермическая реакция) , поэтому константа равновесия будет уменьшаться, а равновесие будет смещаться в сторону исходных веществ. Если , то константа равновесия реакции не зависит от температуры.

В небольшом интервале температур T₂ – T₁ тепловой эффект реакции можно принять постоянным и независящим от температуры. Тогда в интегральной форме уравнение изобары (2.41) принимает вид

. (2.44)

Выражение (2.44) позволяет вычислить константу равновесия при заданной температуре, если известно ее значение при другой температуре, а также тепловой эффект реакции . Если же известны константы равновесия при двух температурах, то можно рассчитать тепловой эффект реакции.

П р и м е р. Упругость диссоциации (равновесное парциальное давление диоксида углерода) при 500 C равна 60 Па, а при 600 C – 440 Па. Вычислить тепловой эффект реакции разложения магнезита

(2.45)

и рассчитать температуру, при которой упругость диссоциации будет равна 1,01310⁵ Па.

Решение. Определяем из уравнения (2.44)

(2.46)

или с учетом (2.34)

, (2.47)

где ; – константы равновесия, выраженные через упругости диссоциации при соответствующих температурах.

Подставив в (2.47) числовые значения, получим

.

Определим температуру T₂, воспользовавшись, например, выражением (2.47), при которой упругость диссоциации достигнет давления 1,01310⁵ Па:

.