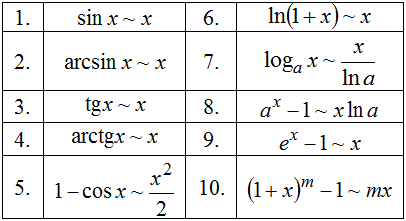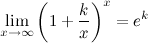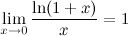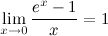15. Взаимное расположение плоскостей в пространстве.
α1IIα2
II
α1⅃α2 ⅃ ,
*
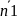=0
Расстояние от точки до плоскости
D=
Угол между двумя плоскостями:
Cosα=
16. Предел ф-ции. Св-ва пределов.
Точку (действительное число) a называют пределом (значений) функции f(x) x О X, в точке х0 ( или, что то же самое, при x à x0 ); если для любой последовательности точек xn О X ; n = 1,2,… , имеющей своим пределом точку x0 , последовательность значений функции в этих точках, т.е. { f(xn) }, имеет своим пределом точку a.
Замечание. Существование предела у всех последовательностей { f(xn) } является необходимым и достаточным условием существования предела функции.
Свойства пределов:
Предел суммы/разности двух функций равен сумме/разности их пределов:
Предел произведения двух функций равен произведению их пределов:
Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:
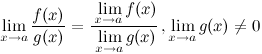
Константу можно выносить за знак предела:
Предел степени с натуральным показателем равен степени предела:
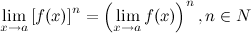
17. Бесконечно малые ф-ции и их св-ва.
Функция
называется
бесконечно
малой функцией (б.м.ф.)
при
(или
в точке
),
если
Основные свойства бесконечно малых функций:
Сумма конечного числа б.м функций является функцией б.м.
Произведение б.м функции на ограниченную есть функция б.м.
Произведение двух б.м функций есть функция б.м.
Произведение б.м функции на константу является б.м функцией.
Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
Функция
,
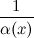обратная к б.м функции
,
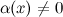есть функция бесконечно большая. Верно
и обратное.
Теорема.
Пусть
-
предел
функции
в
точке
:
.
Тогда заданную функцию можно представить
в виде
,
где
-
б.м функция. Верно и обратное утверждение.
18. Первый замечательный предел. Второй замечательный предел.
Первый замечательный предел:
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
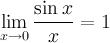
Следствия из первого замечательного предела:
Второй замечательный предел:
,
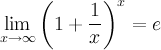здесь е - число
Эйлера.
Следствия из второго замечательного предела:
19. Сравнение бесконечно малых функций. Таблица эквивалентности.
Функция называется бесконечно малой при (или в точке ), если
Бесконечно малые функции одного порядка:
Пусть
и
-
две б.м. функции при
.
Функции
и
называются
б.м. одного порядка малости при
,
если
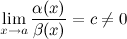
Бесконечно малые функции более низкого и высокого порядков:
1)Если
,
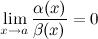то
является
б.м. более
высокого порядка
при
,
чем
,
а
-
б.м. более
низкого порядка по сравнению с
:
при
.
2)Если
,
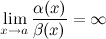то
-
б.м. низшего
порядка малости при
по
сравнению с
.
3) Если
,
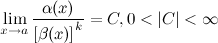то
называется
б.м. порядка
по
сравнению с
при
.
Б.м. функции
и
называются
эквивалентными
или равносильными
б.м. одного порядка при
,
если
Обозначают:
при
.
Таблица эквивалентных
б.м. функций при
