5. Определение векторов. Действия над ними.

Вектором называется направленный отрезок или упорядоченная пара чисел.

2 вектора называются коллинеарными, если они лежат на одной прямой или на II прямых. Коллинеарные вектора А и В называются сонаправленными, когда их направления совпадают и вектора противоположнонаправлены, если у них направления противоположны. Длиной вектора АВ называется число равное отрезку АВ. Два вектора считаются равными, если длины этих векторов одинаковы и они сонаправлены. Если длина вектора а равна 1, то а называется единичным. А₁В₁ называется проекцией вектора АВ на прямую l и находится по формуле: А₁В₁=IABIcosf. Если А имеет координаты Х_а и У_а, а В (Х_в У_в), то длина вектора АВ находится по формуле: IABI= , IaI=

Сложение векторов:

А) правило параллелограмма б) правило треугольника

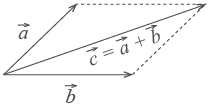
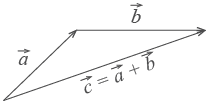
Вычитание векторов:

Произведение на число k: k = - необходимое достаточное условие коллинеарности векторов.

Два вектора IIодной и той же плоскости и лежащие в ней называются компланарными.

6. Скалярное произведение векторов.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

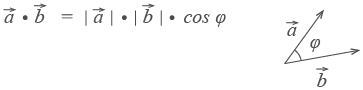
Если векторы перпендикулярны, их скалярное произведение равно нулю.

Из формулы для скалярного произведения можно найти угол между векторами:

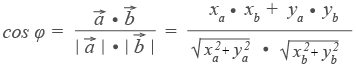
Свойства:

1. =

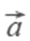
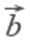2. K( )=(k ) = (k )

3. ( ) = ( )= ( )

4. ( + ) = +

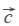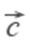5. = ²

7. Векторное произведение векторов.

Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c.

a × b = i j k = i(aybz - azby) - j(axbz - azbx) + k(axby - aybx)

ax ay az

bx by bz

S_парал = a × b

SΔ = 1 |a × b|

2

Свойства:

1. a × b = -b × a

2. (k a) × b = a × (k b) = k (a × b)

3. (a + b) × c = a × c + b × c

4. a×a=0

5. Для того чтобы два нулевых вектора были коллинеарны, необходимо и достаточно, чтобы их скалярное произведение было =0

8. Смешанное произведение векторов.

Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

a · [b × c] = ax ay az

bx by bz

cx cy cz

Геометрический смысл смешанного произведения: если тройка векторов правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: . В случае левой тройки смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: . Если , и компланарны, то их смешанное произведение равно нулю.

- объём пирамиды

Свойства:

1. Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.

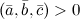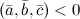2. Тройка векторов является правой тогда и только тогда, когда . Если же , то векторы , и образуют левую тройку векторов.