Вопросы к экзамену по математике

1. Определители 2-го и 3-го порядка. Св-ва определителей.

2. Решение систем линейных алгебраических уравнений методом Крамора. Решение систем линейных однородных алгебраических уравнений.

3. Действия над матрицами и их св-ва.

4. Обратная матрица. Решение систем линейных алгебраических уравнений матричным методом.

5. Определение векторов. Действия над ними.

6. Скалярное произведение векторов.

7. Векторное произведение векторов.

8. Смешанное произведение векторов.

9. Уравнение прямой с заданным угловым коэффициентом. Уравнение прямой, проходящей через 2 точки.

10. Общее уравнение прямой на плоскости.

11. Параметрическое и каноническое уравнения прямой на плоскости.

12. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой.

13. Уравнение плоскости в пространстве. Взаимное расположение прямых в пространстве.

14. Взаимное расположение прямой и плоскости в пространстве.

15. Взаимное расположение плоскостей в пространстве.

16. Предел ф-ции. Св-ва пределов.

17. Бесконечно малые ф-ции и их св-ва.

18. Первый замечательный предел. Второй замечательный предел.

19. Сравнение бесконечно малых функций. Таблица эквивалентности.

20. Общее определение производной.

21. Геометрический смысл производной.

22. Связь между дифференцируемостью и непрерывностью ф-ции.

23. Основные правила дифференцирования. Таблица производных.

24. Логарифмическое дифференцирование.

25. Производная сложной ф-ции.

26. Производная неявной ф-ции.

27. Дифференциал ф-ции, св-ва. Его геометрический смысл.

28. Правило Лопиталя.

29. Необходимое и достаточные условия локального экстремума ф-ции одной переменной.

30. Асимптоты графика ф-ции.

31. Исследование ф-ции на выпуклость и вогнутость. Точки перегиба.

32. Первообразная и неопределённый интеграл. Св-ва неопределённого интеграла.

33. Таблица интегралов.

34. Правила интегрирования.

35. Непосредственное интегрирование.

36. Интегрирование методом замены переменной.

37. Интегрирование по частям.

38. Интегрирование простейших рациональных дробей.

39. Интегрирование некоторых классов тригонометрических ф-ций.

40. Основные св-ва определённого интеграла.

41. Формула Ньютона-Лейбница.

42. Замена переменной в определённом интеграле.

43. Интегрирование по частям определённого интеграла.

44. Приложение определённого интеграла.

45. Комплексные числа.

1. Определители 2-го и 3-го порядка. Св-ва определителей.

Определитель – это числовая характеристика матрицы.

Общий знаменатель значений неизвестных легко выражается через элементы матрицы: он равен произведению элементов главной диагонали минус произведение элементов второй диагонали. Это число называется определителем матрицы, причем, как говорят, определителем второго порядка. Произведения a11a22 и a12a21 называются членами определителя второго порядка. Вычисление определителя 2-гопорядка иллюстрируется схемой:

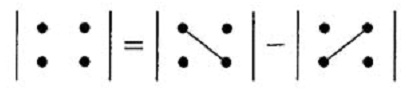
Итак, матрица есть таблица чисел, а определитель – число, соответствующее матрице. Числитель выражений имеет такой же вид, как и знаменатель, т. е. это тоже знаменатель второго порядка. Числитель выражения для x1 есть определитель матрицы, получающейся из матрицы заменой ее первого столбца столбцом из свободных членов системы, а числитель выражения для x2 есть определитель матрицы, получающейся из матрицы такой же заменой ее второго столбца. Таким образом, формулы в новых обозначениях записываются в следующем виде:

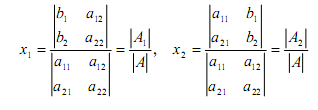
Определитель 3-го порядка.

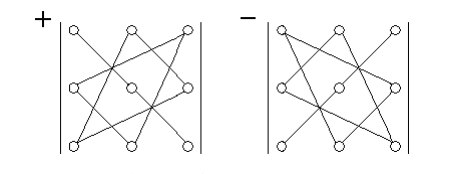
Семь основных свойств определителя 3-го порядка.

Определители третьего порядка (как и определители 2-го порядка) обладают

следующими семью свойствами:

1. определитель не изменится, если строки его матрицы сделать столбцами, а столбцы

строками (определитель не меняется при транспонировании.);

2. при перестановке двух строк определителя он меняет знак;

3. если в определителе имеются две одинаковые строки, то определитель равен нулю;

4. общий множитель определителя строки можно вынести за знак определителя;

5. если элементы одной строки определителя пропорциональны элементам другой, то определитель равен нулю;

6. если к одной строке определителя прибавить другую, умноженную на любое число,

то определитель не изменится.

7. если все элементы какой-то строки или столбца равны 0, то и определитель равен 0.

Замечание. Все свойства остаются справедливыми, если вместо строк взять

столбцы.