12. Шкалирование и виды шкал.

13. Меры разброса.

2. Меры разброса

Дисперсия – это мера вариации значений признака в среднем и вокруг средней арифметической. Фактически это сумма квадратов остатков, деленная на число наблюдений.

Для того чтобы вычислить значение дисперсии, надо вычесть из каждого наблюдаемого значения среднее, возвести в квадрат все полученные отклонения, сложить квадраты отклонений и разделить полученную сумму на n:

где х – каждое наблюдаемое значение признака;

х (с черточкой сверху) – среднее арифметическое значение признака (переменной х);

n – количество наблюдений.

Чтобы сделать соответствующую точечную оценку дисперсии несмещенной, величина объема выборки в знаменателе уменьшается на 1.

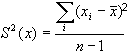
где х_i – каждое наблюдаемое значение признака;

х (с черточкой сверху) – среднее арифметическое значение признака (переменной х);

n – количество наблюдений.

В зависимости от того, насколько велика (мала) дисперсия, или среднеквадратическое отклонение, мы можем судить, насколько единодушны были в своих оценках респонденты (при меньшем значении дисперсии), или насколько сильно они расходятся в своих мнениях (при большем значении дисперсии).

Недостатком дисперсии является то, что это величина безразмерная. Мы можем понять размер доходов и единицы измерения остатков, но в данном случае дисперсия равна 4 000 000. Вряд ли можно сказать большая это величина или маленькая. Кроме того, данное значение не позволяет определить качество модели среднего, поскольку в формуле расчета дисперсии остатки берутся в квадрате.

Для того чтобы преодолеть эти трудности, существуют два производных от дисперсии показателя –

стандартное (среднеквадратичное) отклонение и

стандартная ошибка среднего.

Стандартное отклонение – это корень квадратный из дисперсии:

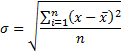
где х_i – каждое наблюдаемое значение признака;

х (с черточкой сверху)– среднее арифметическое значение признака (переменной х);

n – количество наблюдений.

Очевидной интерпретацией стандартного отклонения является его способность оценивать «типичность» среднего: тем меньше, чем лучше среднее представляет совокупность.

Зная значение среднеквадратического отклонения, можно сравнивать меры рассеяния разных признаков или одного признака для различных совокупностей. Прямое сравнение дисперсий и среднеквадратических отклонений без сопоставления со средними арифметическими является бессмысленным.

Интерпретировать данные показатели в совокупности можно следующим образом. Пример: Допустим, нами были рассчитаны среднее арифметическое и среднеквадратическое отклонения затрат времени на домашнюю уборку для нескольких групп женщин: домохозяек (х=6, σ=4), предпринимателей (х=4,5, σ=3,5), служащих (х=5,4 σ=3,5), временно не работающих (х=6, σ=2)⁴. Из полученных данных видно, что женщины-домохозяйки и женщины, временно не работающие, затрачивают на домашнюю уборку в среднем одинаковое время, но совокупность домохозяек менее однородна, потому что среднеквадратическое отклонение больше. Женщины-служащие затрачивают на домашнюю уборку в среднем больше времени, чем женщины предприниматели (дисперсия одинакова в этих группах). Когда средние и дисперсии в сравниваемых группах различны, то необходимо рассчитать коэффициент вариации.

Коэффициент вариации определяется просто как процент наблюдений, лежащих вне модального интервала, т. е. процент (доля) наблюдений, не совпадающих с модальным значением. Например, если от модального отличаются 60% значений, то V=60% (или V=0,6).

Наряду со стандартным отклонением для оценки разброса используется и стандартная ошибка среднего. Основной причиной ее активного использования является то, что в интервале (среднее значение) ± две стандартных ошибки среднего должно находиться 95 % от числа всех значений анализируемой переменой.

Так, например, по результатам исследования мы выяснили, что средний доход респондентов равен 3 275 руб., значение стандартной ошибки среднего составило 132 руб.

Следовательно, можно говорить, что не менее 95 % всех значений дохода, указанных респондентами, должно лежать в интервале 3 275±2*132, т.е. от 3 011 до 3 539 руб.

Наиболее распространенным показателем, характеризующим разброс значений порядковой переменной, является квартильное отклонение.

Для того чтобы понять его смысл, надо уточнить понятие квартиля. Если медиана делит всю совокупность опрошенных на две части – те, кто отметил градации меньше или равно этой точки, и те, кто отметил градации больше этой точки.

Квартильное разбиение делит всех респондентов на 4 части. Так, 1 квартиль – это значение переменной, меньше которой ответили 25 % респондентов, 2-й квартиль – это медиана, 3-й квартиль – точка, меньше которой ответили 75 % респондентов (табл. 5.5).

Таблица 5.5. Распределение ответов респондентов на вопрос

«Оцените, в какой мере В.В. Путину присуще качество

“традиционный”?» (фрагмент приложения программы SPSS)

		Frequency / Частота	Percent / Процент	Valid Percent / Валидный процент	Cumulative Percent / Кумулятивный/ суммарный процент
Valid Валидные	1,00	65	8,1	8,7	8,7
	2,00	57	7,1	7,6	16,3
	3,00	107	13,3	14,3	30,5
	4,00	182	22,7	24,3	54, 8
	5,00	100	12,5	13,3	68,1
	6,00	84	10,5	11,2	79,3
	7,00	155	19,3	20,7	100,0
	/ Итого	750	93,5	100,0
Missing / Пропущенные	System / Без ответа	52	6,5
Total / Итого		802	100,0

Из табл. 5.5 видно, что 1-й квартиль имеет значение 3; 2-й квартиль – значение 4; 3-й квартиль – значение 6.

Квартильное отклонение – это разница между 1-м и 3-м квартилями. В данном случае отклонение составляет 3. При том, что переменная насчитывает 7 градаций, квартильное отклонение, равное 3, может рассматриваться как достаточно большое. Следовательно, модель средней тенденции не очень хорошо отражает поведение нашей переменной, т.к. много респондентов имеют значения, отличающиеся от медианы.

Кроме того, можно производить разбиение совокупности значений на любое количество равных частей. 5 частей – квинтельное разбиение, 10 частей – децильное разбиение.

Применительно к ним можно использовать и такие меры разброса, как квинтельное отношение или децильное отношение.

На примере распределения ответов респондентов на вопрос о доходе вычислим децильное отношение. Для этого построим таблицу, отражающую децили распределения дохода (табл. 5.6).

Таблица 5.6. Децили распределения переменной «Доход»

(фрагмент приложения программы SPSS)

Statistics

Доход

	Valid / Валидные	290
	Missing / Пропущенные	10
Percentiles / Процентили	10	1500,0000
	20	1700,0000
	30	2000,0000
	40	2500,0000
	50	2800,0000
	60	3000,0000
	70	3425,0000
	80	4000,0000
	90	6000,0000

Из таблицы видно, что доход, равный 1 500, имеют 10 % респондентов (граница 1 дециля), 10 % опрошенных получают доход 6 000 и выше (граница 10 дециля).

Децильное отношение – это отношение границы 10-го дециля к границе 1-го дециля. Данный показатель демонстрирует то, насколько больше получают 10 % высокооплачиваемых респондентов в сравнении с 10 % наименее оплачиваемых. Данное отношение в нашем примере составляет 4, что показывает степень неоднородности доходов.