20.Пружинный, физический и математический маятники.

Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под воздействием упругой силы.

Уравнение движения пружинного маятника:

Физический маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс C тела.Если маятник отклонен из положения равновесия на некоторый угол , то момент возвращающей силы равен: (где I – момент инерции маятника относительно какой-то оси, - расстояние между точкой подвеса и центром масс маятника, - возвращ. сила ( “-” обозначает, что направление и всегда противоположны) ) . При малых колебаниях физич. маятник совершает гармонич. колебания с циклич. частотой и периодом , где - приведенная длина физич. маятника.Математический маятник – это идеализированная система, состоящая из материальной точки массой , подвешенной на невесомой нерастяжимой нити, и колеблющаяся под действием силы тяжести. Момент инерции математического маятника . Так как вся масса матем. маятника сосредоточена в одной точке – центре масс, то период маятника равен Приведенная длина математического маятника – это длина такого математич. маятника, период колебаний которого совпадает с периодом колебаний

21.Сложение гармонических колебаний одного направления и одинаковой частоты.

Сложим гармонич. колебания одного направления и одинаковой частоты и построим векторные диаграммы этих колебаний Т.к. векторы А1 , А2 -вращаются с одинаковой угловой скоростью, то разность фаз будет постоянной. . В этом выражении амплитуда А и начальная фаза  задаются соотношениями Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой что и складываемые колебания. Амплитуда зависит от разности фаз.В результате сложения колебаний мало отличающихся по частоте получаются колебания с периодически меняющейся амплитудой.

22.Сложение взаимно перпендикулярных колебаний.Рассмотрим результат сложения колебаний одинаковой частоты ,происходящих во взаимно перпендикулярных направлениях. Начальную фазу первого колебания примем = 0.

2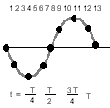 3.Продольные и поперечные волны. Уравнение бегущей волны. Процесс образования поперечных волн следует рассматривать так : пусть имеется ряд точек (1...13), расположенных на прямой, и точка 1 под влиянием внешнего воздействия в момент t=0 начала совершать гармоническое поступательное движение с периодом Т по направлению, перпендикулярно му этой прямой (поперечная волна). Всего будет 5-ть рисунков. Первый, когда t=0… Поперечные упругие волныраспространяются в средах, в котор ых возникают упругие силы при деформации сдвига, т.е. в твёрдых телах. Рассмотрим образование продольных волн. Точка 1 в некоторый момент t=0 приходит в колебание вдоль луча, двигаясь влево. Продольная волна представляет собой чередующиеся сгущения и разряжения витков пружины. Волна называется продольной, если частицы среды совершают колебания в направлении распространения волны. Вид волны зависит от вида деформации. Продольные волны обусловлены линейной деформацией (сжатия-растяжения), поперечные волны – деформацией сдвига. Продольн ые волны образуются как в твёрдых, так и в жидких и газообразных телах.

24.Образование стоячих волн. Уравнение стоячей волны и его анализ. Стоячее волны — это волны, образ.при наложении 2х бегущих воли, распростр.навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и одинаковой поляризацией.

Для вывода уравнения стоячей волны предположим, что две плоские волны распространяются навстречу друг другу вдоль оси х в среде без затухания, причем обе волны характеризуются одинаковыми амплитудами и частотами. Кроме того, начало координат выберем в точке, в которой обе волны имеют одинаковую начальную фазу, а отсчет времени начнем с момента, когда начальные фазы обеих волн равны нулю. Тогда соответственно уравнения волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, будут иметь вид

Сложив эти уравнения и учитывая, что k=2v/X (см. (154.3)), получим уравнение стоячей волны:

25.Уравнение молекулярно-кинетической теории идеального газа для давления и его сравнение с уравнением Менделеева-Клапейрона.Пусть некоторая масса газа занимает объём V1 ,имеет давление р1 , и находится при тем-ре Т1 .Эта же масса газа в другом произвольном состоянии характеризуется параметрами (V2 р2 Т2) переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: изотермического и изохорного.В соответствии з законами Бойля-Мариота и Гей-Люссака : Где R молярная газовая постоянная R=KNA=8,31дж/(моль*К). В равных объёмах идеальных газов при равных давлениях и температурах содержится одинаковое кол-во молекул. Для массы m газа .

26.Степень свободы молекул. Распространение энергии по степеням свободы молекул.Число степеней свободы – это число независимых величин с помощью которых может быть задано положение системы. (1 атом =3 ст., 2 атома =5ст. 3 атома=6ст.) Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная КТ/2 , а на каждую колебательную – КТСредняя энергия молекулы Внутренняя энергия для 1 моля для массы m газа