14.Момент импульса относительно точки. Момент импульса относительно неподвижной оси вращения.

Закон сохранения момента импульса:

Моментом импульса относительно неподвижной оси называется скалярная величина , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки данной оси . Значение момента не зависит от выбора положения точки на оси . Моментом импульса материальной точки относительно неподвижной точки О наз. физ. величина, определяемая векторным произведением: , где – радиус-вектор проведенный из точки в точку .Модуль момента импульса: .

15.Момент инерции тела относительно оси.

Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс 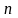материальных точек системы на квадраты их расстояний до рассматриваемой оси: . В случае непрерывного распределения масс эта сумма сводится к интегралу .Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой оси вращения определяется теоремой Штейнера: 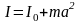, где – расстояние между осями.

17.Кинетическая энергия вращающегося тела.

Кинетическая энергия вращательного тела:

_{Кинетическая энергия вращения} разобьём тело на маленькие объёмы с элементарными массами m находящиеся на расстоянии r от оси вращения. При подвижной оси эти объёмы опишут окружности различных радиусов r и имеют различные скорости V, но угловая скорость этих объёмов одинакова . Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объёмов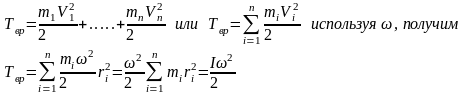 В случае плоского движения тела скатывающегося с наклонной плоскости, без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения.

18.Закон сохранения момента импульса.

При вращении материальной точки или системы материальных точек вокруг неподвижной оси момент импульса отдельной частицы: .Момент импульса системы материальных точек относительно оси: .Продифференцировав по времени получим: , т. е. .В замкнутой системе момент внешних сил и , откуда 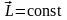.Это выражение представляет собой закон сохранения импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Этот закон является следствием изотропности пространства (одинаковости свойств пространства по всем направлениям).

19.Гармонические механические колебания и их кинематические характеристики.

Колебаниями наз. движения или процессы, которые характеризуются определенной повторяемостью во времени. Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). где А - амплитуда колебаний (максимальное значение колеблющейся величины) ,  0 – круговая (циклическая) частота,  - начальная фаза колебаний в момент времени t=0, ( 0 t+)- фаза колебаний в момент времени t. Периодом колебаний наз. промежуток времени Т, через который состояние системы повторяется. Для гармонических колебани Частота колебаний – число полных колебаний,совершаемых в единицу времени. Записав первую и вторую производные по времени от гармонически колеблющейся величины s (скорость и ускорение): ускорение смещение находятся в противофазе, т.е. когда смещение достигает положительного наибольшего значения, ускорение достигает наибольшего по величине отрицательного значения и наоборот.