ГОУ Санкт-Петербургский государственный Политехнический университет

Институт прикладной математики и механики

Отчет по лабораторной работе

«Определение напряженно-деформированного состояния композитного узла»

Вариант: 14

Выполнила: студентка группы 53602/1

Коковцева Анна Валерьевна

Санкт-Петербург

2014 г.

Ход работы и получение результатов

Определение упругих модулей композита.

Постановка задачи

Для определения упругих модулей композита рассмотрим ячейку элементарного представительного объема (рис. 1).

2a = 4.577мкм

2a = 4.577 мкммкм мкм мкм мкм мкм

d = 4 мкм

Рис. 1. Элементарный представительный объем

Свойства компонент представлены в таблице 1.

Табл. 1. Свойства компонент материала

Компонент	Е, Па	ν	G, Па
1 - матрица	4∙109	0.45	1.3793∙109
2 - волокно	250∙109	0.30	96.1538∙109

На основе алгоритма конечно-элементного определения эффективных характеристик волокнистых композитов и конечно-элементного решения с помощью пакета ANSYS серии задач для ячейки периодичности композитной структуры необходимо вычислить:

– эффективные упругие модули Юнга

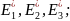
– эффективные коэффициенты Пуассона

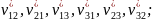
– эффективные модули сдвига

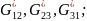
Аналитическое решение.

Для определения эффективного модуля Юнга используется правило смесей:

где 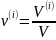– объемная концентрация i-го компонента, – модуль Юнга i-го компонента, N – количество компонентов.

Для рассматриваемой ячейки: . Подставив полученные значения, найдем .

Эффективные модули Юнга 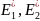и коэффициенты Пуассона определяются из опыта на одноосное растяжение, в ходе которого должны быть получены средние значения напряжений, возникающих в ячейке периодичности композита:

Также используются соотношения связи:

Для определения эффективного модуля сдвига необходимо решить задачу о поперечном сдвиге ячейки периодичности. Искомый модуль сдвига определяется из эффективных упругих соотношений для ортотропной среды:

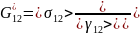
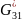Для определения эффективных модулей сдвига и необходимо решить две задачи о продольном сдвиге ячейки периодичности. Искомые модули сдвига определяются из эффективных упругих соотношений:

Для первой задачи:

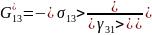
Для второй задачи:

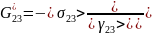
Конечно-элементная постановка задачи

Для получения средних значений напряжений решим численно задачу о растяжении ячейки периодичности методом конечных элементов. Построим модель средствами пакета КЭ анализа ANSYS. В силу симметрии будем рассматривать только четверть представительного объема:

A

B

D

C

Рис. 2. Графическое представление КЭ модели ячейки

При построении модели использованы восьмиузловые квадратичные плоские элементы (каждый узел обладает двумя трансляционными степенями свободы).

Определение эффективных модулей Юнга и коэффициентов Пуассона

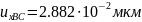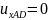
Зададим горизонтальное перемещение правой границы расчетной области , а остальные зафиксируем , обеспечив тем самым деформацию .

И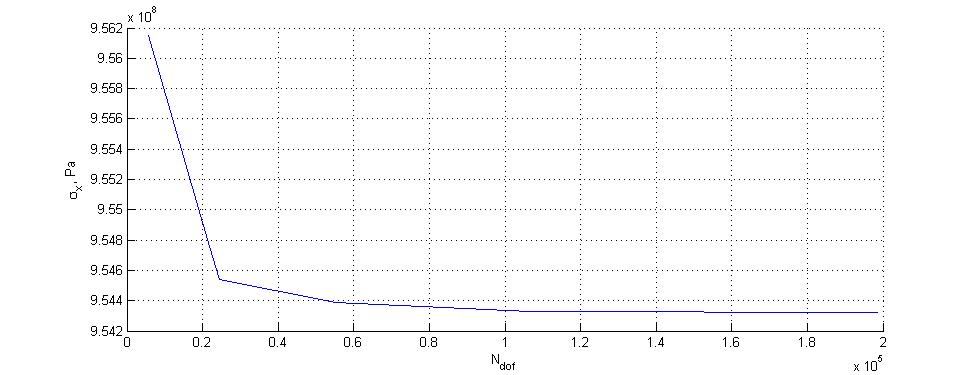 сследуем сходимость решения поставленной задачи по методу конечных элементов, проведя несколько расчетов на различных сетках. В качестве контрольного параметра выберем значение напряжений в нижней правой точке ячейки. По результатам серии вычислительных экспериментов построим зависимость решения от числа степеней свободы КЭ модели:

Рис. 3. График сходимости МК

Как видно, метод достаточно быстро сходится, и решение практически перестает меняться уже при количестве степеней свободы модели .

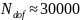Задав размеры КЭ сетки, обеспечивающие удовлетворительную точность, получим окончательное решение. Результаты представим графически в виде полей перемещений и напряжений ячейки:

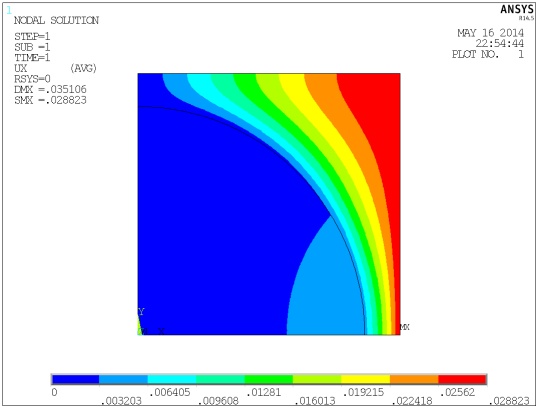
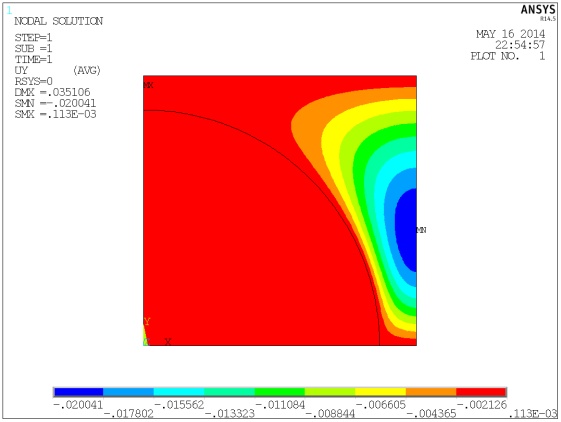
Рис. 4. Поля перемещений и

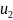
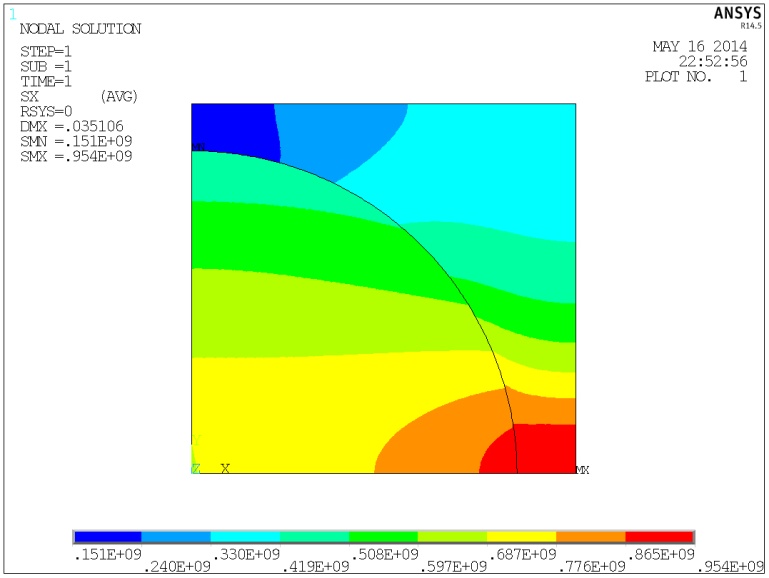
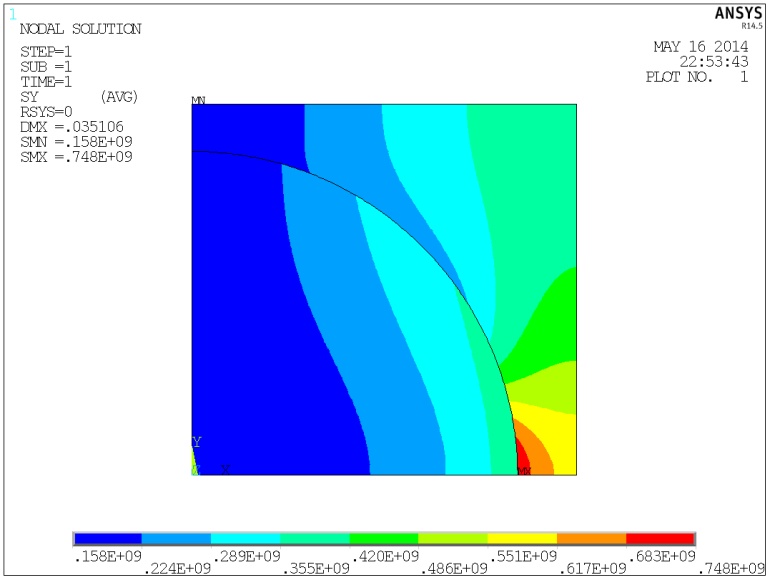
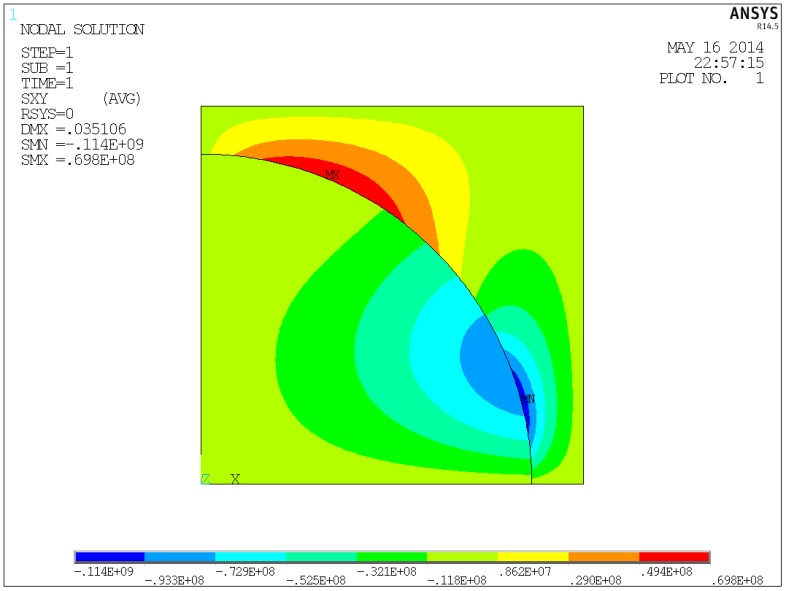
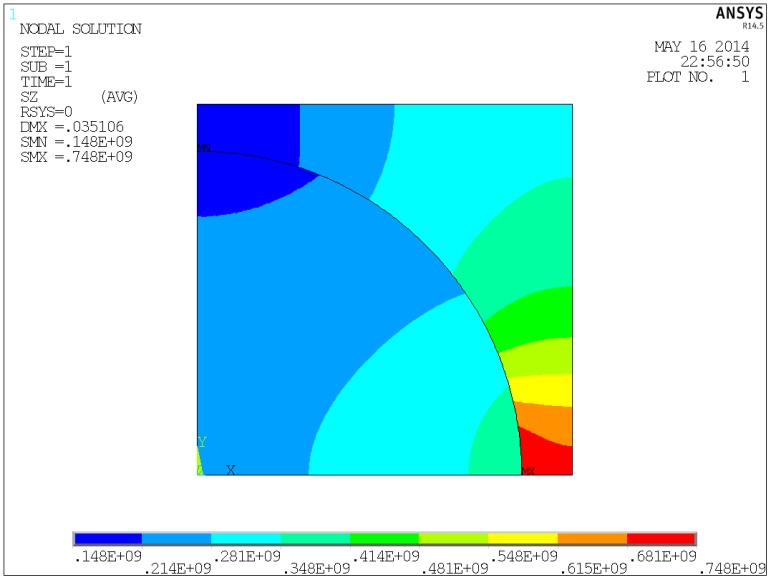
Рис. 5. Поля нормальных 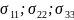и касательных напряжений

Средние значения напряжений:

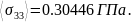
Решив систему линейных алгебраических уравнений относительно неизвестных , получим: