1. Системы идентификации и аутентификации пользователей

Применяются для ограничения доступа случайных и незаконных пользователей к ресурсам компьютерной системы. Общий алгоритм работы таких систем заключается в том, чтобы получить от пользователя информацию, удостоверяющую его личность, проверить ее подлинность и затем предоставить (или не предоставить) этому пользователю возможность работы с системой.

2. Системы шифрования дисковых данных

Чтобы сделать информацию бесполезной для противника, используется совокупность методов преобразования данных, называемая криптографией [от греч. kryptos- скрытый и grapho - пишу].

3. Системы шифрования данных, передаваемых по сетям

Различают два основных способа шифрования: канальное шифрование и оконечное (абонентское) шифрование.

В случае канального шифрования защищается вся информация, передаваемая по каналу связи, включая служебную. Этот способ шифрования обладает следующим достоинством - встраивание процедур шифрования на канальный уровень позволяет использовать аппаратные средства, что способствует повышению производительности системы.

4. Системы аутентификации электронных данных

При обмене данными по сетям возникает проблема аутентификации автора документа и самого документа, т.е. установление подлинности автора и проверка отсутствия изменений в полученном документе. Для аутентификации данных применяют код аутентификации сообщения (имитовставку) или электронную подпись.

5. Средства управления криптографическими ключами

Безопасность любой криптосистемы определяется используемыми криптографическими ключами. В случае ненадежного управления ключами злоумышленник может завладеть ключевой информацией и получить полный доступ ко всей информации в системе или сети.

28. Технология автоматизированного офиса. Автоматизированные рабочие места (арм). Арм ветеринарного врача.

Автоматизи́рованное рабо́чее ме́сто (АРМ) — программно-технический комплекс, предназначенный для автоматизации деятельности определенного вида. При разработке АРМ для управления технологическим оборудованием как правило используют SCADA-системы.

АРМ объединяет программно-аппаратные средства, обеспечивающие взаимодействие человека с компьютером, предоставляет возможность ввода информации (через клавиатуру,компьютерную мышь, сканер и пр.) и её вывод на экран монитора, принтер, графопостроитель, звуковую карту — динамики или иные устройства вывода. Как правило, АРМ является частью АСУ.

Базой новых информационных технологий в области ветеринарии являются персональные компьютеры. Стационарные компьютеры устанавливают в административных зданиях хозяйств и предприятий, на их базе создают автоматизированные рабочие места (АРМ) ветеринарных врачей на фермах, в цехах. С помощью портативных компьютеров автоматизируются информационные процессы при обслуживании отдельных производственных участков, кооперативов и фермерских хозяйств. Функциональное назначение программного комплекса — автоматизация процессов учета, планирования, диагностики, лечения, профилактики, экономики и отчетности

30. Основные понятия теории вероятностей. Пространство элементарных исходов и случайные события

Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятностей является понятие случайного события (или просто события).

Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.

Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств. Такой подход называется теоретико-множественным.

Достоверным называется событие W, которое происходит в каждом опыте.

Невозможным называется событие Æ, которое в результате опыта произойти не может.

Несовместными называются события, которые в одном опыте не могут произойти одновременно.

Суммой (объединением) двух событий A и B (обозначается A+B, AÈB) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.

Произведением (пересечением) двух событий A и B (обозначается A×B, AÇB) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.

Противоположным к событию A называется такое событие  , которое заключается в том, что событие A не происходит.

События A_k (k=1, 2, ..., n) образуют полную группу, если они попарно несовСлучайные события и их классификация, операции над событиями.

Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.

При преобразовании выражений можно пользоваться следующими тождествами:

.

На основе вышеизложенного сформулированы аксиомы теории вероятностей. Пусть каждому событию ставится в соответствие число, называемое вероятностью события. Вероятность события A обозначается P(A). Так как событие есть множество, то вероятность события есть функция множества. Вероятности событий удовлетворяют следующим аксиомам.

1. Вероятность любого события заключена между нулем и единицей:

(1.1)

2. Если A и B несовместные события, то

(1.2)

Вторая аксиома обобщается на любое число событий: 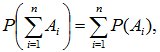  если события А_i и A_j попарно несовместны для всех i≠j

События A₁, A_2, …, A_n называют равновозможными если

P(A₁)=P(A₂)= … =P(A_n). (1.3)

Если в каком-то опыте пространство элементарных событий Ω можно представить в виде полной группы несовместных и равновозможных событий ω₁, ω₂, …, ω_n, то такие события называютсяслучаями, а сам опыт сводится к схеме случаев.

Случай ω_i называется благоприятным событием A, если он является элементом множества A:  .

Классическое определение вероятности: вероятность события определяется по формуле

 , (1.4)

где n - число элементарных равновозможных исходов данного опыта;

m - число равновозможных исходов, приводящих к появлению события.

31. Распределение хи-квадрат.

Распределение хи-квадрат применяется для проверки статистических гипотез.

где m-эмпирические частоты

m¹- теоретические частоты

n- число степеней свободы

При полном совпадении эмпирических частот с частотами вычисленными или ожидаемыми хи-квадрат равен 0 если же не равно 0 это укажет на несоответствие вычисленных частот эмпирическим частотам ряда. В таких случаях необходимо оценить значимость критерия хи-квадрат которое теоритически может изменяться от 0 до ∞ это производится путем сравнения его фактически полученного значения с его критическим значением. Гипотеза отвергается если хи-квадрат ≥ критического значения для принятого уровня значимости и числа степеней свобод.

Для определения критерия хи-квадрат необходимо найти теоретические частоты-равновероятные частоты- сложение всех частот и деление на количество категорий.

Для определения стандартного значения хи-квадрат число степеней свободы

где R – количество строк в таблице

С количество столбцов

32. Распределение Стьюдента.

Представляет собой сумму нескольких нормальных распределений случайных величин. Высчитывается по формуле для нахождения критерий. Полученные значения сравнивают до стандартного значения таблицы Стьюдента с учётом вероятности и числа степеней свободы.

33. Распределение Фишера.

Данное распределение нашло применение при построение интервальных оценок и статистических критериев, отношение двух выборочных дисперсий вычисленных по двум выборкам извлеченных из одной генеральной совокупности. Если имеются 2 случайных величины X и Y подчиняющихся закону распределения хи-квадрат со степенями свободы a и b соответственно то отношение - распределение Фишера, f- распределение с числом степеней свободы a и b.

34. Коэффициент корреляции.

Коэффициент корреляции показывает степень статистической зависимости между двумя числовыми переменными. Коэффициент корреляции варьирует от -1 до 1. При отрицательном показателе: при увеличение одного признака показатель другого признака снижается. При положительном: при повышении одного признака повышается и другой.

35. Двумерное нормальное распределение.

2 переменные имеют двумерное нормальное распределение если для каждого фиксированного значения одной переменной имеется соответствующее значение другой переменной. Свойственно для биологических признаков.

36. Статистические данные. Понятие генеральной совокупности и случайной выборки.

Статистические данные  — это совокупность объектов (наблюдений, случаев) и признаков (переменных), их характеризующих. Генеральная совокупность- большое количество исследуемых наблюдений. Выборка- случайная совокупность испытуемых из общего числа, тех на которых можно будет распространять полученные в результате изучения совокупности.

37. Переменные и наблюдения, количественные, номинальные и ранговые переменные.

Переменные- характеристики изучаемых объектов. Наблюдения- числовые или номинальные данные переменных.

Номинальные переменные- нечисловые, означают принадлежность к классам, не могут быть использованы при вычислениях или упорядочены.

Количественные- выражены в единицах измерения; например, вес, рост, кровяное давление, число приступов астмы в определенный период и т.п.

Ранговые- данные упорядочены но не могут быть с уверенностью измерены и сопоставлены. К таким переменным применимы ранговые методы.

38. Статистическое оценивание. Понятие статистической оценки.

Статистическое оценивание подразделяют на точечное и интервальное.

Статистическая оценка - некоторая функция от результатов наблюдений, предназначенная для статистического оценивания неизвестных характеристик и параметров распределения вероятностей.

Статистические оценки — это статистики, которые используются для оценивания неизвестных параметров распределений случайной величины.

Основной целью статистического оценивания является определение действительных параметров генеральной совокупности на основе изучения выборочных показателей При этом выборка должна достаточно хорошо воспроизводить свойства генеральной совокупности.

39. Метод максимального правдоподобия. Точечное оценивание характеристик распределения.

В математической статистике это метод оценивания неизвестного параметра путем максимизации функции правдоподобия. Основан на предположении о том , что информация по статической выборке содержится в функции правдоподобия. Применяется в моделировании ситуаций, максимально достоверен в случае нормального распределения показателя.

Точечной оценкой для математического ожидания в силу закона больших чисел является выборочное среднее арифметическое  . В некоторых случаях могут быть использованы и другие оценки. Например, если известно, что распределение симметрично относительно своего центра, то центр распределения является не только математическим ожиданием, но и медианой, а потому для его оценки можно использовать выборочную медиану.

40. Интервальное оценивание. Доверительный интервал для средней арифметической генеральной совокупности.

Интервальное оценивание- способ получения оценки для неизвестного значения скалярного параметра с помощью интервала его допустимых значений определяющих вероятности того что в этом интервале находится истинное значение параметра. Среднее квадратичное отклонение (σ)характеризует однородность вариационного ряда , если σ мало значит ряд однороден и рассчитанное среднее арифметическое достаточно верно характеризует данный вариационный ряд, если σ велико то ряд неоднородный и полученное значение среднего арифметического характеризует не весь ряд, а какую-то его часть.

Теоритическое распределение вариант подчиняется правило 3σ. Все что лежит ( в биологических исследованиях) в пределах X±3σ – доверительный интервал. Крайние значения признака в пределах доверительного интервала- границы изменчивости генеральной совокупности- лимиты.

41. Ошибки репрезентативности.

Ошибками репрезентативности называют расхождения между средними величинами или долями признака выборочной и генеральной совокупности. Они присущи только несилошным наблюдениям. Ошибки репрезентативности могут быть:

систематическими;

случайными.

Систематическими называются ошибки, которые возникают из-за нарушения научного принципа отбора единиц в выборочную совокупность. Они возникают в тех случаях, когда в результате неправильного отбора в выборочную совокупность попали наилучшие или наихудшие единицы.

В результате такого отбора средние и относительные показатели, полученные по выборочной совокупности, будут искаженно характеризовать генеральную совокупность.

Случайные ошибки репрезентативности – это неточности, которые возникают из-за того, что выборочная совокупность не совсем правильно отражает средние величины и величины доли признака генеральной совокупности. Такие ошибки возникают даже при самом строгом соблюдении принципов и правил отбора единиц в выборочную совокупность.

Ошибки репрезентативности свойственны только выборочному наблюдению. Они не могут быть полностью устранены, но они могут быть доведены до незначительных размеров, если соответствующим образом организовать отбор единиц в выборочную совокупность.

Пределы ошибок репрезентативности можно определить с достаточной степенью точности на основании ряда теорем в теории вероятности и математической статистике.

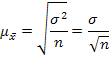
Ошибка репрезентативности - расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности.

Систематические ошибки репрезентативности - ошибки, возникающие в связи с особенностями принятой системы отбора и обработки данных на¬блюдений или в связи с нарушением установленных правил отбора.

Случайные ошибки репрезентативности ошибки, возникающие в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности.

42. Дескриптивные и графические методы анализа данных.

. Описательное (дескриптивное) исследование в оценке проводится для того, чтобы описать то, как реализовывалась программа, какие мероприятие были проведены, какие ресурсы были затрачены, какие результаты достигнуты и т. п. Данный вид исследования не оценивает конкретно качественные или количественные характеристики программы, оно оптимизирует набор данных характеристик и оценивает программу, как с качественной, так и с количественной стороны. Дескриптивная статистика пытается выявить причину возникновения того или иного явления, касательно программы и эффект, появившийся в связи с этим явлением. Типы вопросов, которые ставятся в ходе оценивания программы, позволяют достаточно точно провести исследование и сделать выводы.

Описательное (дескриптивное) исследование может быть как качественным, так и количественным. В данном исследовании могут совмещаться как числовые, так и качественные данные, которые в ходе исследования могу быть объединены, так и разделены, в зависимости, от того какая характеристика программы оценивается. Данные, полученные в ходе описательного исследования, могут группироваться в таблицы, графики, а также интерпретироваться в описательной форме. Дескриптивное исследование позволяет придавать данным более удобные для проведения оценки программ вид. Данный вид исследования оптимизирует коллекцию данных и методы оценки, с помощью нахождения статистических характеристик и взаимосвязей между данными, что позволяет проводить оценивание более эффективными способами

43. Общая характеристика программного обеспечения анализа данных на персональных компьютерах.

Введение. Общее понятие ПО для ПК.

Персональный компьютер, как известно, является универсальным устройством для обработки информации. Персональные компьютеры могут выполнять любые действия по обработке информации. Для этого необходимо составить для компьютера на понятном ему языке точную и подробную последовательность инструкций – программу, как надо обрабатывать информацию.

При своем выполнении программы могут использовать различные устройства для ввода и вывода данных, подобно тому, как человеческий мозг пользуется органами чувств для получения и передачи информации. Сам по себе ПК не обладает знаниями ни в одной области своего применения, все эти знания сосредоточены в выполняемых на нем программах.

В настоящее время весь комплекс ПО делится на системные и пользовательские программы. Системное программное обеспечение выполняет функции «организатора» всех частей ПК, а также подключенных к нему внешних устройств. Программы для пользователей служат для выполнения, каких – либо конкретных задач во всех сферах человеческой деятельности.

По функциональному признаку различают следующие виды ПО:

• Системное;

• Общее;

• Специальное.

Под системным (базовым) понимается ПО, включающее в себя операционные системы, сетевое ПО, сервисные программы, а также средства разработки программ (трансляторы, редакторы связей, отладчики и пр.).

Основные функции операционных систем (ОС) заключаются в управлении ресурсами (физическими и логическими) и процессами вычислительных систем. Физическими ресурсами являются: оперативная память, процессор, монитор, печатающее устройство, магнитные и оптические диски. К логическим ресурсам можно отнести программы, файлы, события и т.д. под процессом понимается некоторая последовательность действий, предписанная соответствующей программой и используемыми ею данными.

Сетевое ПО предназначено для управления общими ресурсами в распределенных вычислительных системах: сетевыми накопителями на магнитных дисках, принтерами, сканерами, передаваемыми сообщениями и т.д. к сетевому ПО относят ОС, поддерживающие работу ПК в сетевых конфигурациях (сетевые ОС), а также отдельные сетевые программы (пакеты), используемые совместно с обычными, не сетевыми ОС.

Оболочки операционных систем предоставляют пользователю качественно новый интерфейс по сравнению с реализуемым операционной системой. Такие системы существенно упрощают выполнение часто запрашиваемых функций, например, операций с файлами. В целом, программы-оболочки заметно повышают уровень пользовательского интерфейса, наиболее полно удовлетворяя потребностям пользователя.

Программное обеспечение общего назначения используется для решения определенной целевой задачи из проблемной области. Часто такие программы называют приложениями, а программное обеспечение - прикладным. Прикладное ПО может использоваться в промышленном производстве, инженерной практике, научных исследованиях, медицине, управление, делопроизводстве, издательской деятельности, образовании и т.д.

44. Создание и редактирование документов в текстовом редакторе MS Word.

В окне программы Microsoft Word нет отдельного окна документа с самостоятельными строкой заголовка и кнопка­ми свертывания, восстановления или развертывания. Если в приложении открыт один документ, то в правой части строки меню присутствует кнопка закрытия (рис. 2). Если же откры­то несколько документов, то этой кнопки нет. Если все доку­менты закрыты, то можно увидеть «чистое» окно программы (рис. 3).

Чем же, однако, испещрено наше «чистое» окно? Это встро­енные в Microsoft Word панели инструментов, выведенные на экран. Основная цель картинки — показать, что самостоя­тельное окно программы Microsoft Word существует, и непре­менными его атрибутами являются строка заголовка, стро­ка меню, панель команд и панель документа. Панель доку­мента — это область, занимаемая документом и освобожда­емая при закрытии последнего открытого документа. Область между строкой заголовка и панелью документа — панель команд. Строка меню всегда присутствует в окне программы.