13. Объем тела по площади поперечных сечений. Объем и поверхность тела вращения.

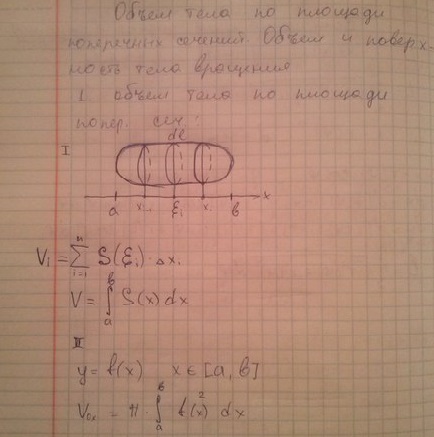
14. Вычисление координат центра тяжести кривой и криволинейной трапеции.

Определение. Центром тяжести тела называется такая точка  , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.

Обозначим через   и   расстояния центра тяжести кривой от осей ординат и абсцисс.

Тогда, пользуясь определением центра тяжести кривой, получим:

Разрешая полученные равенства относительно   и  , найдем координаты центра тяжести плоской кривой 

Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.

Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.

Пример 1. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью  . Тогда статический момент полуокружности относительно диаметра выразится формулой

, где   — дифференциал дуги кривой  .

В выбранной системе координат уравнение полуокружности запишется так:  . Тогда

 и потому  .

Следовательно,

Пример 2. Найдем центр тяжести четверти окружности  , расположенной в первом квадранте.

Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому  . Достаточно найти только  .

Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:

Отсюда находим, что   и

Поскольку длина   четверти данной окружности равна  , то

Вычисление статических моментов и координат центров тяжести плоских фигур

Н айдем статический момент прямоугольника со сторонами   и   относительно стороны  . Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны   и   (рис. 61). Масса элементарного прямоугольника равна его площади   (напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен  , а статический момент всего прямоугольника равен

(1)

Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой  , где   — непрерывная и неотрицательная функция на отрезке  , снизу осью абсцисс, а с боков прямыми  .

Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно   и высота  . Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен  , а потому статический момент всей криволинейной трапеции равен  . В случае, когда не выполняется предположение о неотрицательности функции  , эту формулу надо заменить такой: (части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в  ).

Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу  , а потому ордината центра тяжести этой трапеции выражается формулой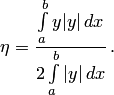

Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно  . Поэтому его статический момент равен  , а статический момент всей трапеции выражается формулой . Следовательно, абсцисса центра тяжести выражается так:  .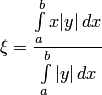

Пример 3. Найти статический момент (относительно оси  ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:

Решение. Так как параметр   одной арки циклоиды изменяется от   до  , то

Пример 4. Найти центр тяжести фигуры, ограниченной осью   и одной полуволной синусоиды  .

Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой  , то центр тяжести лежит на этой прямой и, следовательно,  . Ордината   центра тяжести находится по формуле  .

Так как 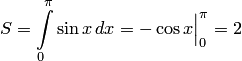 , то  .

Итак, центр тяжести данной фигуры находится в точке  .

Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды  .

Решение. Данная фигура расположена симметрично относительно прямой  , следовательно, центр тяжести ее находится на этой прямой, и потому  . Найдем   по формуле  .

Площадь   данной фигуры была вычислена раньше, она равна  . Следовательно,

Центр тяжести данной фигуры находится в точке  .

15. Задачи о работе силы и давления жидкости на пластину.

16. Несобственный интеграл первого рода и признаки их сходимости, примеры.

17. Необственный интеграл второго рода и признаки их сходимости, примеры.

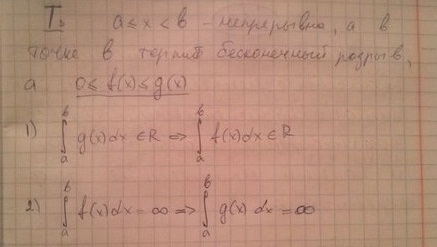
18. Основные понятия функций нескольких переменных: предел, непрерывность, частные производные, дифференциалы частные и полный. Применение дифференциала.

19. Геометрический смысл уравнения z=f(x,y). Касательная плоскость и нормаль.

20. Частные производные сложных функций и полная производная. Дифференцирование неявно заданных функций.

21. Экстремумы функций z=f(x,y); необходимые и достаточные условия экстермума.

22. Скалярное поле. Поверхности уровня. Производная по направлению и градиент.

23. Дифференциальные уравнения первого порядка. Теорема Коши. Уравнения с разделяющимися переменными.

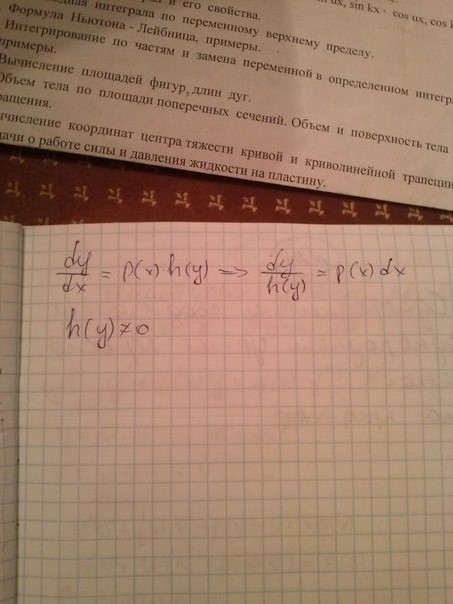
24. Однородные и сводящиеся к однородным уравнения первого порядка.

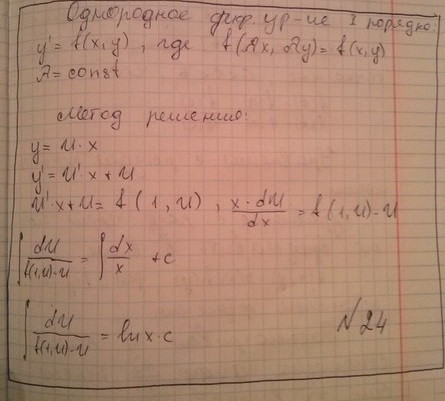
25. Линейные уравнения первого порядка к Бернулли

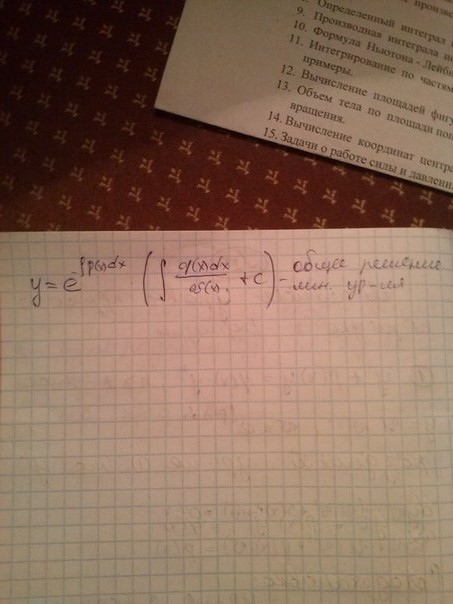
26. Дифференциальные уравнения, допускающие понижение порядка.

27. Линейные однородные уравнения второго порядка с постоянными коэффициентами.

28. Линейные неоднородные уравнения второго порядка со специальной правой частью.

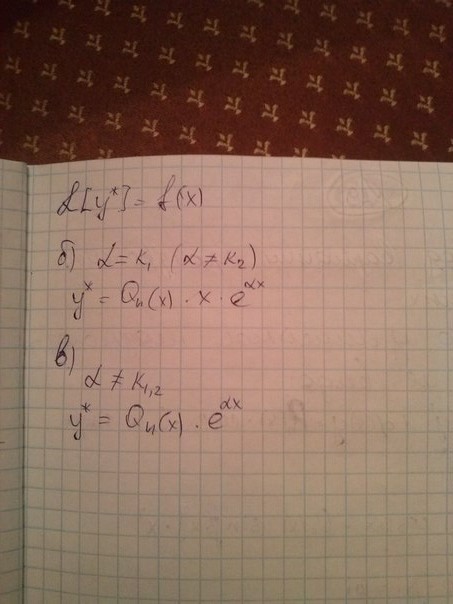
29. Метод вариации произвольных постоянных.

30. Системы дифференциальных уравнений. Метод исключения.