9. Производная интеграла по переменному верхнему пределу.

Если f(x)- непрерывная функция и Ф(x)=∫^x_a f (t) dt, то имеет место равенство Ф'(x)=f (x). Иными словами, производная от опред интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела( при условии, что подынтегральная функция непрерывна). В частности, следует, что всякая непрерывная функция имеет первообразную. Доказательство: дадим аргументу х положительное или отриц приращение ∆x; тогда: Ф(x+∆x)=∫^x+∆x_a f (t) dt=∫^x_a f (t) dt+∫^x+∆x_x f (t) dt. Приращение функции Ф(х) равно: ∆Ф= Ф(x+∆x)- Ф(х)=∫^x_a f (t) dt=∫^x+∆x_х f (t) dt-∫^x_а f (t) dt, т.е.∆Ф=∫^x+∆x_х f (t) dt. К последнему интегралу применим теорему о среднем значении: ∆Ф= f(ξ)( x+∆x-x)= f(ξ)∆x, где ξ заключено между х и x+∆x. Найдем отношение приращения функции к приращению аргумента ∆Ф/∆x= f(ξ)∆x/∆x= f(ξ). Следовательно, Ф'(x)=lim_∆x→0∆Ф/∆x= lim_∆x→0 f(ξ). Но так как ξ→x при ∆x→0, то lim_∆x→0 f(ξ)=lim _ξ→x f(ξ), а вследствии непрерывности функции f(x): lim _ξ→x f(ξ)=f(x). Таким образом, Ф'(x)=f(x). Теорема доказана.

10. Формула Ньютона — Лейбница, примеры.

Если F(x) есть какая-либо первообразная от непрерывной функции f(x), то справедлива формула: ∫^b_a f (x) dx=F(b)-F(a)=F(x)l^b_a. Эта формула наз формулой Ньютона-Лейбница.Доказательство: Пусть F(x) есть некоторая первообразная от функции f(x). Функция ∫^х_a f (t) dt первообразная от f(x). Но две любые первообразные от данной функции отличаются на постоянное слагаемое С. Следовательно, можно написать: ∫^х_a f (t) dt=F(x)+C. Это равенство при соответствующем выборе С справедливо при всех значениях х, т.е. является тождеством. Для определения постоянного С положим в этом тождестве х=а; тогда ∫^а_a f (t) dt=F(а)+C, или 0= F(а)+C, откуда С= -F(a). Следовательно, ∫^х_a f (t) dt=F(x)- F(a). Полагая х=b, получим формулу Ньютона-Лейбница или, заменив обозначение переменной интегрирования на х. Пр.1). ∫^b_a x dx=x²/2l^b_a=(b²-a²)/2; 2)∫^2π₀ sinxdx= -cosxl ^2π₀= -(cos 2π- cos0)=0

11. Интегрирование по частям и замена переменной в определенном интеграле, примеры.

Замена переменной. Пусть дан интеграл: ∫^b_a f (x) dx, где функция f(x) непрерывна на отрезке [a,b]. Введем новое переменное t по формуле х=φ(t). Если 1)φ(α)=а, φ (β)=b,2)φ(t) и φ'(t) непрерывны на отрезке [α,β], 3) f[φ(t)] определена на отрезке [α,β], то ∫^b_a f (x) dx=∫^β _α f[φ(t)] φ'(t)dt. Пр. ∫³₂ dx/x²+2x+5=∫³₂ d(x+1)/(x+1)² +4=1/2*arctg(x+1)/2 l³₂=1/8; a=arctg1/8

По частям.Пусть u и v- дифференцируемые функции от x. Тогда (uv)'=u'v+uv'. Интегрируя обе части тождества в пределах от a до b, получим: ∫^b_a (uv)' dx=∫^b_a u'v dx=∫^b_a uv' dx. Так как∫ (uv)' dx= uv+C, то ∫^b_a (uv)' dx=uvl^b_a; поэтому равенство может быть записано в виде: uvl^b_a=∫^b_a vdu+∫^b_a udv,или окончательно ∫^b_a udv= uvl^b_a - ∫^b_a vdu. Пр.∫^0.5₀ х²е^хdx=[u=x², du=2xdx, dv=e^xdx,v=e^x]= x²e^xl^0.5₀ - ∫^0.5₀ 2xе^хdx=[x=u, du=dx,е^хdx=dv, v=e^x]= ...=5e^0.5/4 – 2.

12. Вычисление площадей фигур, длин дуг.

Вычисление площадей в прямоугольных координатах.

1. Если на отрезке [a,b] функция f(x)>=0, то (по определению интеграла как предела интегральной суммы функции), площадь криволинейной трапеции, ограниченной кривой y=f(x), осью Ox и прямыми x=a и x=b равна:

2. 

3. Если на отрезке [a,b] функция f(x)<=0, то определенный интеграл также <=0. По абсолютной величине он равен площади S соответствующей криволинейной трапеции.

2.

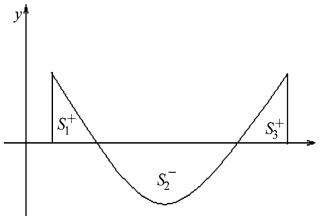
Если f(x) конечное число раз меняет знак на отрезке [a,b], то интеграл по всему отрезку [a,b] разбиваем на сумму интегралов по частичным отрезкам. Для того чтобы получить площадь, нужно найти сумму абсолютных величин интегралов по частичным отрезкам или вычислить интеграл:

3.

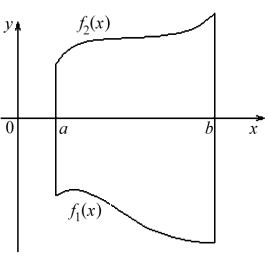
Если нужно вычислить площадь области, ограниченной кривыми y=f₁(x), y=f₂(x) и ординатами x=a, x=b, то при условии f₁(x)>=f₂(x) будем иметь:

Если нужно вычислить площадь области, ограниченной кривыми x=f₁(y), x=f₂(y) и абсциссами y=c, y=d, то при условии f₁(y)>=f₂(y) будем иметь:

4. Площадь криволинейной трапеции в случае, если кривая задана уравнениями в параметрической форме: , где . Пусть уравнения определяют некоторую функцию y=f(x) на отрезке [a,b] и, следовательно, площадь криволинейной трапеции может быть вычислена по формуле:

Сделаем замену переменного в этом интеграле: . На основании уравнений получим . Следовательно,

Вычисление площадей в полярных координатах.

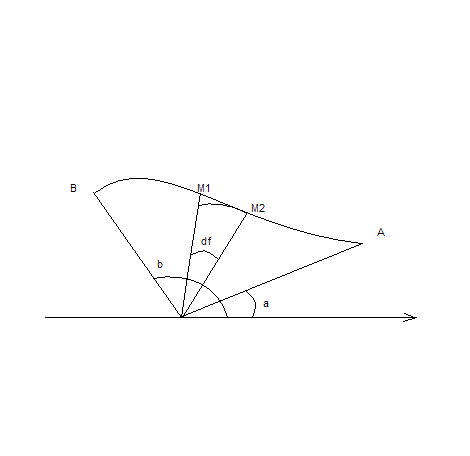
Вычисление площади криволинейного сектора. Пусть кривая AB зада-на в полярных координатах уравнением , , причем  непрерывная и неотрицательная на отрезке функция. Фигуру, ограниченную кривой AB и двумя полярными радиусами, составляющими с полярной осью углы , будем называть криволинейным сектором.

Разобьем данную область (криволинейный сектор) на n частей. Частичный сектор М₁М₂ заменяем круговым. Его площадь равна Сумма площадей n частей (секторов) даст площадь ступенчатого сектора. Так как эта сумма является интегральной суммой для функции на отрезке , площадь криволинейного сектора равна:

Вычисление длины дуги плоской кривой

Д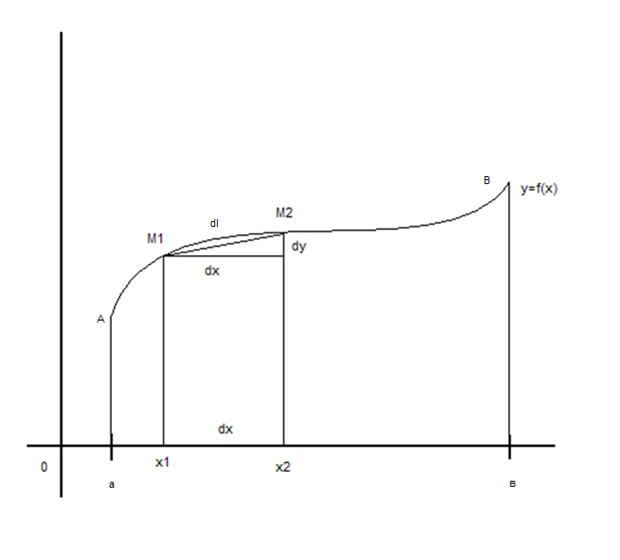 лина дуги – предел вписанной в эту дугу ломаной линии при неограниченном увеличении числа ее звений и стремлении к нулю наибольшей длины частичного звена.

Вычисление длины дуги, когда задано все явно:

Вычисление длины дуги, когда уравнение кривой задано в параметрической форме:

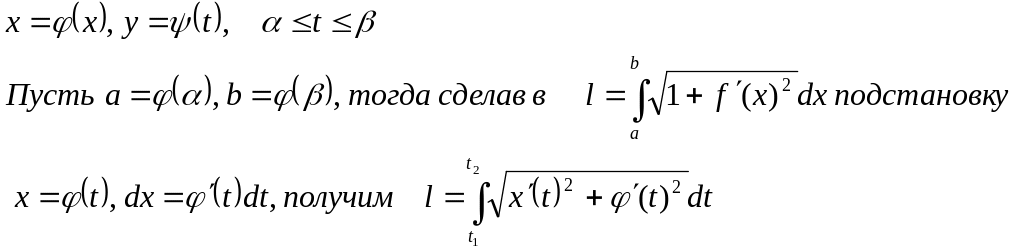
Вычисление длины дуги, заданной в полярных координатах: