72. Статистичний розподіл вибірки,дискретний варіаційний ряд,полігон частот

Статистичним рядом називають вибірку обсягу одержану з генеральної сукупності. Він підлягає подальшій обробці та аналізу.

Перший етап обробки статистичного ряду – ранжування – запис елементів у порядку їх зростання (неспадання), в результаті якого отримують так званий простий варіаційний ряд, елементами якого є де

Наступний етап обробки – побудова статистичного (емпіричного) закону розподілу.

Якщо – дискретна випадкова величина, найбільш природна форма статистичного закону розподілу вибірки описується за допомогою згрупованого варіаційного ряду.

Згрупований варіаційний ряд отримано на основі простого варіаційного ряду шляхом відбору всіх різних елементів, та розміщення їх у порядку зростання: де

Для виділених варіант одночасно обчислюють частоти що їм відповідають, або відносні частоти

(3.1)

Очевидно, що

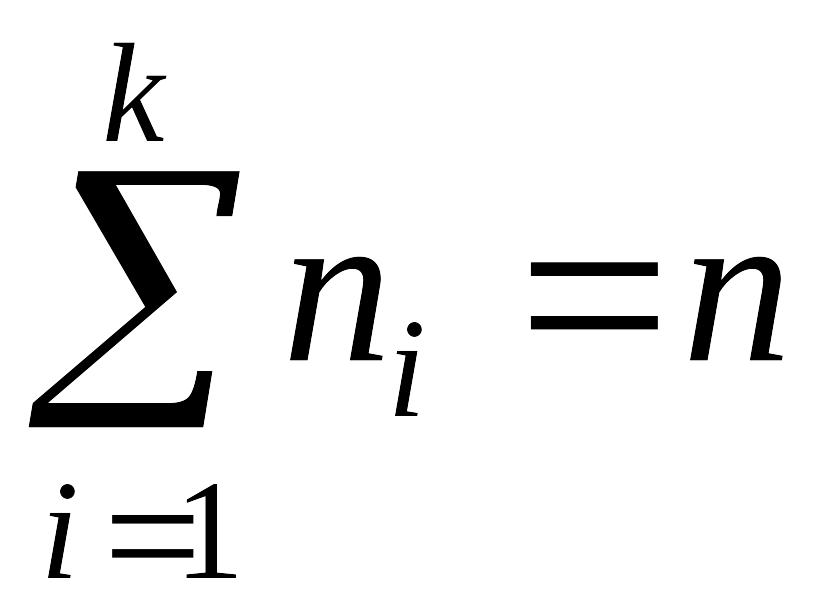, (3.2) (3.3)

Дискретним статистичним розподілом вибірки називається відповідність між варіантами та їх частотами або відносними частотами.

Дискретний статистичний розподіл подають у формі таблиць 3.1-3.2:

• дискретний статистичний розподіл частот:

Таблиця 3.1

			…
			…

• дискретний статистичний розподіл відносних частот:

Таблиця 3.2

			…
			…

73. Статистичний розподіл вибірки,інтервальний варіаційний ряд,полігон частот

Якщо – неперервна випадкова величина (а також у випадку, коли випадкова величина дискретна й обсяг вибірки відносно великий: ) статистичний закон розподілу вибірки записують як інтервальний варіаційний ряд частот або відносних частот.

Інтервальним статистичним розподілом вибірки називається відповідність між інтервалами варіаційного ряду та їх частотами або відносними частотами (або щільністю відносних частот).

Схема побудови інтервального статистичного розподілу вибірки:

• статистичні дані ранжують;

• визначають оптимальний інтервал довжиною h – такий, при якому інтервальний ряд не був би великим і в той же час дозволяв виявити характерні риси досліджуваного явища.

Довжину інтервалу знаходимо як відношення розмаху варіації до числа інтервалів K:

(3.4)

де число інтервалів наближено обчислюємо за допомогою формули Стерджесса:

(3.5)

Якщо дробове, то за величину можна взяти або найближче ціле число, або найближче нескладне дробове значення. За початок першого інтервалу раціонально взяти

(3.6)

початок другого інтервалу збігається з кінцем першого й дорівнює

(3.7)

і т.д. Цей процес продовжують, поки початок наступного інтервалу не буде більшим (якщо дорівнює, в інтервальному варіаційному ряді останній проміжок – відрізок), ніж

• визначають частоту для кожного інтервалу, тобто число значень випадкової величини, що належать цьому інтервалу, включаючи й значення, що співпали з нижньою межею, але менше верхньої межі;

• визначають відносні частоти:

(3.8)

Інтервальний статистичний розподіл вибірки, як і дискретний, записують у вигляді таблиць 3.3-3.4:

• інтервальний статистичний розподіл частот:

Таблиця 3.3

			…
			…

(3.9)

• інтервальний статистичний розподіл відносних частот:

Таблиця 3.4

			…
			…

(3.10)

Інтервальний статистичний розподіл вибірки за необхідності можна замінити дискретним, для цього в кожному інтервалі обирають його “представника”, тобто знаходять середнє арифметичне:

а відповідні значення частот (відносних частот) залишають без змін.

Полігон розподілу вибірки використовується для зображення як дискретних, так й інтервальних варіаційних рядів, а гістограма – лише для інтервальних рядів.

Полігоном частот називають ламану, відрізки якої послідовно з’єднують точки координатної площини.

Полігоном відносних частот називають ламану, відрізки якої послідовно з’єднують точки координатної площини.

Схема побудови полігона частот (відносних частот):

• на осі абсцис відкладають варіанти 

• на осі ординат – відповідні частоти (відносні частоти );

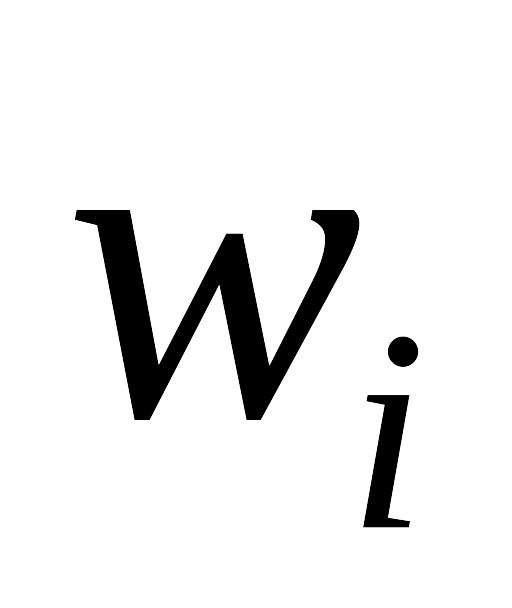• точки ( ) з’єднують відрізками прямих.