Практическая работа №7 Динамическое программирование

Задание: решить задачу распределения капиталовложений. Найти оптимальное распределение инвестиций в объеме 5 млн. руб. между 4 предприятиями так, чтобы максимизировать сумму прибыли.

Х од работы:

S₀= 5 млн.

K – предприятие(1,2,3,4)

X – средства

F_k(x) – прибыль в конце года

S _k - параметр состояния

С умма прибыли равнв :

Переменные X удо влетворяют ограничениям:

Требуется найти такие переменные x1,x2,x3,x4, удовлетворяющие системе и обращающие в максимум функцию.

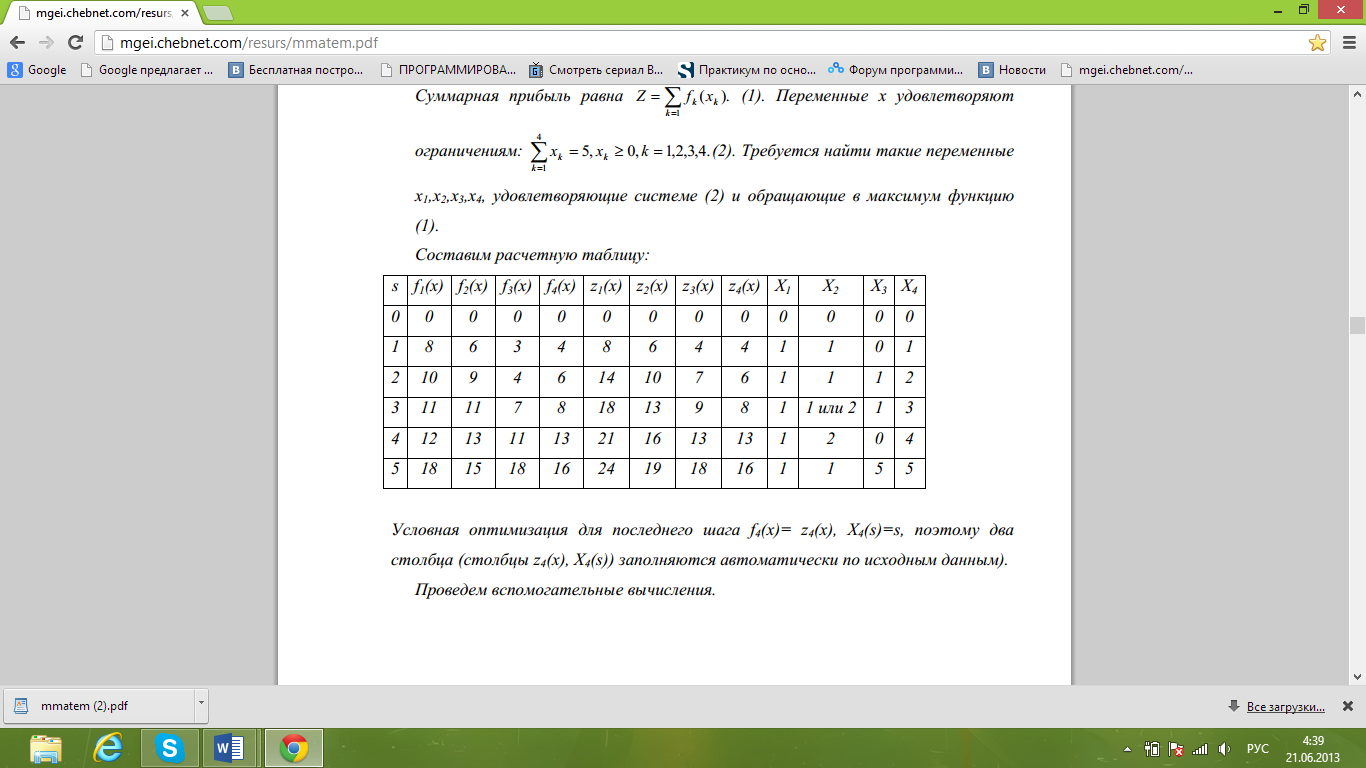
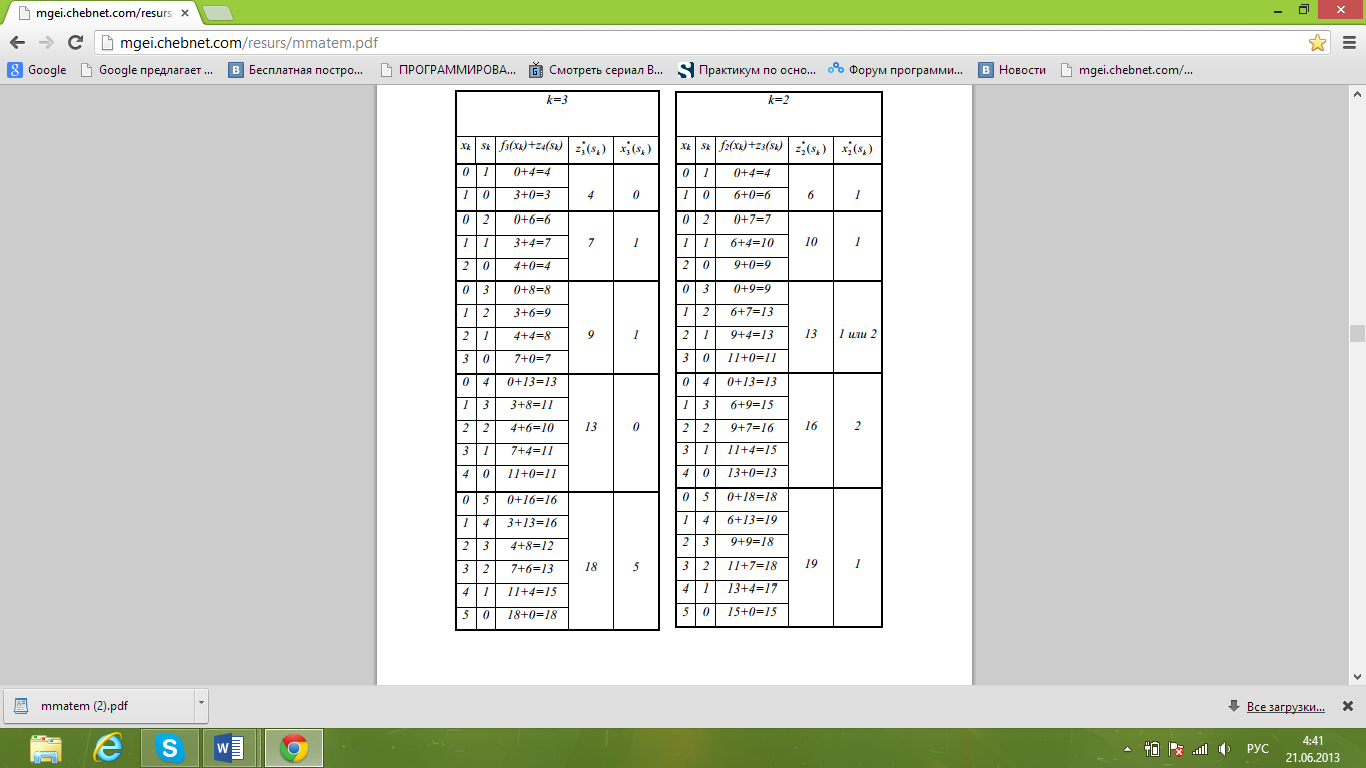
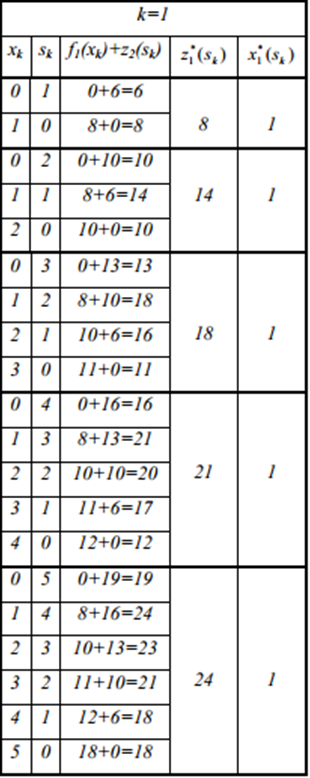
Z_max=z₁^*(5)=24 при x₁= x₁(5)=1

Используя уравнения состояний получим:

S1=5-1=4 при x2=2

S2=4-2=2 при x2=1

S3=2-1=1 при x3=1

X(1,2,1,1)

Вывод: максимум суммарной прибыли равен 24млн.руб, при условии, что выделено:

1. - 1 млн.р

2. - 2 млн.р

3. - 1 млн.р

4. - 1 млн.р

Практическая работа №8 Системы массового обслуживания

Цель : применение на практике знаний о СМО

Задание:

1. Решить задачу определения эффективности телефонной связи при наличии одного телефонного номера. Известно, что заявки на телефонные переговоры поступают с интенсивностью заявок в час, а средняя продолжительность разговора по телефону 2 минуты. Определить показатели эффективности СМО (телефонной связи) при наличии одного телефонного номера (а=105)

2. В условиях предыдущего задания определить оптимальное число телефонных номеров так, чтобы в среднем из каждых 100 заявок не менее 90 было удовлетворено.

Ход работы:

1. Имеем (1/ч) t_об=2 мин

Интенсивность потока U=1/2(1/мин) 30(1/ч)

Q= т.е. в среднем только 22% осуществляют переговоры по телефону.

Вероятность отказа:

P= 1-0,22=0,78

Абсолютно пропускная способность:

A=105*0,22=23,1 т.е. в час будут успешно проведены 23.1 телефонных разговоров.

При наличии одного телефона будет плохо справляться с потоком связи.

2. Интенсивность нагрузки канала:

P= t_об=2мин

N=2,3,4,5…

P₀= (1+3,5+ )^-1=0,1

Q=1-(

A=105*0,375=39,4

Составим таблицу занятости каналов:

	Число каналов
Хар-ка обслуживания	1	2	3	4	5
Отн.Пропускная способность(Q)	0.22	0.37	0.53	0.7	0.87
Абс.Пропускная способность(А)	20.8	39.4	56.6	72.4	87.3

Условие оптимальности: Q

Необходимо установить 4 телефонных номера, при этом буду обслуживаться 72 заявки(А=72.4), а среднее число занятых номеров =

Лабораторная работа №9 Теория игр

Цель: применить знания о «теории игр» на практике

Задание: Решить задачу – определения оптимальной стратегии выпуска видов продукции приведя ее к задаче линейного программирования:

1. Найти решение игры. Данные указаны в таблице:

	B1	B2
A1	2	3
A2	3	5

2. Числовые данные
   xi	-3	2	3	5
   p	0,3	0,4	0,1	0,2

   Решить задачу определения решения игры с использованием теоремы об активных стратегиях: найти решение игры, заданной матрицей: