Ход работы:
|
Обычный станок(Z=2000) |
Станок с программным управлением(Z=5000) |
Всего |
Сталь |
200кг |
700кг |
46000 |
Цветной металл |
200кг |
100кг |
22000 |
|
|
||
Осуществим выбор переменных. Надо указать количество станков каждого вида:
X1 - количество обычных станков
X2 – количество программных станков
Общая прибыль от обычных станков: 2000*x1
Общая прибыль от программных станков: 5000*x2
F(x1,x2)= 2000x1+5000x2 => max
Затраты на сталь: 200x1+700x2 ≤ 46000
Затраты на цветной металл: 200x1+100x2 ≤ 22000
Еще фабрика не может производить отрицательное количество,т.е.
X1≥0
X2≥0
Следовательно математическая модель примет следующий вид:
F(x1,x2)= 2000x1+5000x2 => max
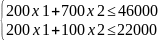
X1≥0
X2≥0
Лабораторная работа№6 Динамическое программирование
Задание:
Найти оптимальное распределение инвестиций в объеме 6млн.руб между 5 предприятиями так,чтобы максимизировать сумму прибыли.
Номера предприятий выбираются из таблицы.
Инвестиции |
Дополнительная прибыль |
П2 |
|
0 |
0 |
1 |
1 |
2 |
4 |
3 |
6 |
4 |
9 |
5 |
11 |
6 |
13 |
Ход работы:
Исходные данные.
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
6 |
9 |
11 |
13 |
I этап. Условная оптимизация. 1-ый шаг. k = 6.
e5 |
u6 |
e6 = e5 - u6 |
f6(u6) |
F*6(e6) |
u6(e6) |
13 |
6 |
7 |
5 |
|
|
|
13 |
0 |
11 |
11 |
13 |
2-ый шаг. k = 5.
e4 |
u5 |
e5 = e4 - u5 |
f5(u5) |
F*5(e4) |
F4(u5,e4) |
F*5(e5) |
u5(e5) |
13 |
6 |
7 |
4 |
11 |
15 |
15 |
6 |
|
13 |
0 |
9 |
0 |
9 |
|
|
3-ый шаг. k = 4.
e3 |
u4 |
e4 = e3 - u4 |
f4(u4) |
F*4(e3) |
F3(u4,e3) |
F*4(e4) |
u4(e4) |
13 |
6 |
7 |
3 |
15 |
18 |
18 |
6 |
|
13 |
0 |
6 |
0 |
6 |
|
|
4-ый шаг. k = 3.
e2 |
u3 |
e3 = e2 - u3 |
f3(u3) |
F*3(e2) |
F2(u3,e2) |
F*3(e3) |
u3(e3) |
13 |
6 |
7 |
2 |
18 |
20 |
20 |
6 |
|
13 |
0 |
2 |
0 |
2 |
|
|
5-ый шаг. k = 2.
e1 |
u2 |
e2 = e1 - u2 |
f2(u2) |
F*2(e1) |
F1(u2,e1) |
F*2(e2) |
u2(e2) |
13 |
6 |
7 |
1 |
20 |
21 |
21 |
6 |
|
13 |
0 |
1 |
0 |
1 |
|
|
6-ый шаг. k = 1.
e0 |
u1 |
e1 = e0 - u1 |
f1(u1) |
F*1(e0) |
F0(u1,e0) |
F*1(e1) |
u1(e1) |
13 |
6 |
7 |
0 |
21 |
21 |
21 |
6 |
|
13 |
0 |
0 |
0 |
0 |
|
|
Поясним построение таблиц и последовательность проведения расчетов. Столбцы 1 (вложенные средства), 2 (проект) и 3 (остаток средств) для всех трех таблиц одинаковы, поэтому их можно было бы сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице 6-го шага столбцы 5 и 6 отсутствуют). В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7. Этап II. Безусловная оптимизация. e1 = e0 - u1 e1 = 13 - 6 = 7 e2 = e1 - u2 e2 = 7 - 0 = 7 e3 = e2 - u3 e3 = 7 - 0 = 7 e4 = e3 - u4 e4 = 7 - 0 = 7 e5 = e4 - u5 e5 = 7 - 0 = 7 Итак, инвестиции в размере 13 необходимо распределить следующим образом: 1-му предприятию выделить 6 2-му предприятию выделить 0 3-му предприятию выделить 0 4-му предприятию выделить 0 5-му предприятию выделить 0 6-му предприятию выделить 7 Что обеспечит максимальный доход, равный 21