
- •Лабораторная работа №1 Решение задач линейного программирования графическим методом
- •Ход работы:
- •Лабораторная работа№2 Решение задач симплекс методом.
- •Лабораторная работа №3 Решение задач двойственным симплекс методом.
- •Ход работы:
- •Лабораторная работа №4 Решение задач на построение оптимального плана.
- •Ход работы:
- •1)Северо-Западный метод:
- •Метод наименьшей стоимости:
- •Лабораторная работа №5 Нахождение оптимального плана при решении задач
- •Ход работы:
- •Лабораторная работа№6 Динамическое программирование
- •Ход работы:
- •Практическая работа №7 Динамическое программирование
- •Х од работы:
- •Практическая работа №8 Системы массового обслуживания
- •Лабораторная работа №9 Теория игр
- •Ход работы:
- •Построение прогнозов количественными методами
- •Ход работы:
Лабораторная работа №1 Решение задач линейного программирования графическим методом
Цель: получение практических навыков при решении задач линейного программирования графическим методом.
Задача№1
Найти оптимальные решение задач линейного программирования
P =2x1+3x2
max
=2x1+3x2
max
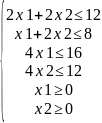
Задача№2
Найти область решений и область допустимых решений а так же определить координаты угловых точек области допустимых решений системы не равенств.
3x1+2x2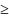 6
6
1x1-x2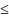 1
1
6x1+ 5x2 30
X1,2 0
Задача №3
Дать математическую постановку и решить графическим методом следующую задачу распределения ресурсов : Предприятие выпускает два вида изделий (И1;И2) на изготовление затрачиваются ресурсы трёх видов (Р1;Р2;Р3) запасы которых равны (А1;А2;А3) соответственно. На изготовление одного изделия первого вида расходуется (10;20;20) ресурсов (Р1;Р2;Р3) а на изготовление одного изделия второго вида (20;10;20) единиц. Каждое изделие первого вида приносит предприятию доход две условные единице, а второго вида три условные единице. Требуется определить в каких количествах надо выпускать изделия первого и второго вида для получения максимального дохода от реализации изделия.
Ход работы:
Задание№1:
2х1+2х2=12 2)х1+2х2=8 3)4х1=16 4)4х2=12
Х1=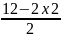 х1=8-2х2
х1=4
х2=3
х1=8-2х2
х1=4
х2=3
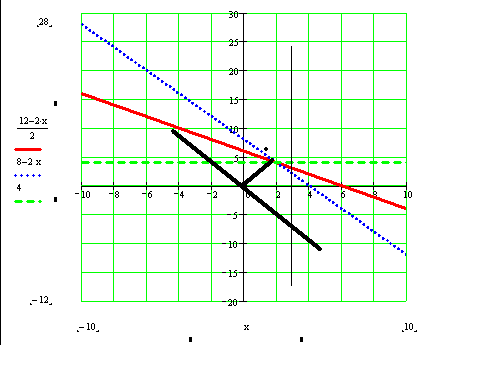
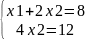 MAX;
MAX;
X2=3;
X1=2;
2)
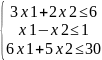 x1,x2
x1,x2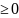
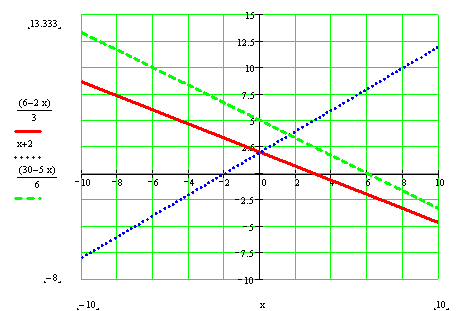
Область допустимых значений на промежутке [0;2].
3)
F(x1,x2)=
2x1+3x2 MAX
MAX
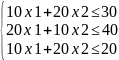 x1,x2
x1,x2
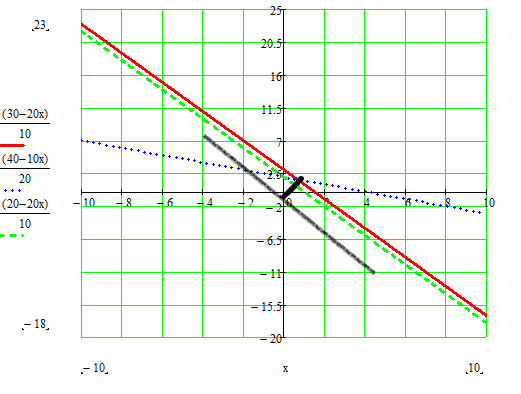
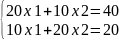 MAX;
MAX;
Точка Max= [-2;8]
Лабораторная работа№2 Решение задач симплекс методом.
Цель: получение практических навыков при решении задач симплекс методом.
Задание:
Предприятие выпускает два вида изделий (И1;И2) на изготовление затрачиваются ресурсы трёх видов (Р1;Р2;Р3) запасы которых равны (А1;А2;А3) соответственно. На изготовление одного изделия первого вида расходуется (10;20;20) ресурсов (Р1;Р2;Р3) а на изготовление одного изделия второго вида (20;10;20) единиц. Каждое изделие первого вида приносит предприятию доход две условные единице, а второго вида три условные единицы. Требуется определить, в каких количествах надо выпускать изделия первого и второго вида для получения максимального дохода от реализации изделия.
Ход работы:
F(x1,x2)= 2x1+3x2 MAX
x1,x2
Представим в канонической форме:
F-2x1-3x2=0
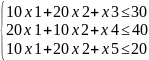 (0,0,30,40,20)
(0,0,30,40,20)
Ci |
Xj |
aij |
X1 |
X2 |
X3 |
X4 |
X5 |
Ai0/aip |
|
X3 |
30 |
10 |
20 |
1 |
0 |
0 |
3 |
|
X4 |
40 |
20 |
10 |
0 |
1 |
0 |
2 |
|
X5 |
20 |
20 |
20 |
0 |
0 |
1 |
1 |
|
f |
0 |
-2 |
-3 |
0 |
0 |
0 |
|
|
X3 |
20 |
0 |
10 |
1 |
0 |
-1/2 |
2 |
|
X4 |
20 |
0 |
-10 |
0 |
1 |
-1 |
- |
2 |
X1 |
1 |
1 |
1 |
0 |
0 |
1/20 |
1 |
|
f |
2 |
0 |
-1 |
0 |
0 |
1/10 |
|
|
X3 |
10 |
-10 |
0 |
1 |
0 |
-1 |
|
|
X4 |
30 |
10 |
0 |
0 |
1 |
-1/2 |
|
3 |
X2 |
1 |
1 |
1 |
0 |
0 |
1/20 |
|
|
F |
3 |
1 |
0 |
0 |
0 |
3/20 |
|
Ответ: X=(0,1,10,30,0) и F max=3
