К специальным относятся карты:

• физико-географические (карты рельефа земной поверхности, почвенные, климатические, растительности, зоогеграфические и др.)

• социально-экономические (политико-административные, населения, экономические, исторические, культурного строительства и др.)

2.5 Масштаб

При составлении планов и измерений на них отрезков линий пользуются масштабами. Масштаб плана – это отношение длины отрезка на плане к соответствующей ему горизонтальной проекции на местности. Масштабы бывают численные и графические.

Дробь, числитель которой равен единице, а знаменатель - числу, показывающему, во сколько раз уменьшены на плане горизонтальные проекции отрезков линий местности, называется численным масштабом (например, 1:1000, 1:5000 и т.д.). Чем больше знаменатель численного масштаба, тем масштаб считается мельче и наоборот. Численный масштаб величина отвлеченная, она не зависит от системы (единиц) линейных мер.

Графические масштабы бывают линейные и поперечные. Линейный масштаб – это графический масштаб в виде масштабной линейки, разделенной на равные части с подписанными значениями соответствующих расстояний на местности. (рис.8) Для более точного построения и измерения отрезков пользуются поперечными масштабами. Поперечный масштаб – графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.

Предельные размеры предметов, различаемые на плане, определяются точностью масштаба. Отрезок t на местности, соответствующий в данном масштабе 0,1 мм плана, называется точностью масштаба, т.е. t=(0,0001m) м, где m – знаменатель численного масштаба.

Преобразование натуральных величин в масштабные и обратно выполняется по принципу составления и решения пропорций, основой которых является заданный масштаб.

Задача: отрезком, какой длины (l_Х) на плане масштаба 1:2000 изобразится линия, имеющая в натуре длину 78м?

Решение: 1 – 2000 (1 ед. На плане соответствует 2000 ед. Натуры)

l_Х – 78 м. (а l_Х ед длины на плане соответствует линия длиной 78м)

l_Х = = 0,039м = 39 мм

Обратная задача: какой длины l_Х в натуре будет линия, изображенная на плане масштаба 1:5000 отрезком длиной 39 мм?

Решение: 1 – 5000 (1 ед. Длины на плане соответствует 5000 ед. Натуры)

39 мм - l_Х (а отрезку длиной 39 мм на плане соответствует l_Х ед натуры)

l_Х = = 195000 мм = 195м

2.6 Номенклатура топографических карт

Система обозначения отдельных листов топографических карт называется номенклатурой карт. С номенклатурой карт вы познакомились при выполнении контрольной работы.

1.9 Изображение рельефа местности на планах и картах

Рельефом называют совокупность различных по форме неровностей (понижений и возвышений) на земной поверхности.

Из всех многообразных форм рельефа земной поверхности можно выделить:

• положительные (выпуклые) курган, бугор, холм, увал, гора, седловина, хребет, плато;

• отрицательные (вогнутые) – овраг, балка, лощина, долина, ущелье, котловина;

В зависимости от абсолютного значения высот точек различают равнинную, холмистую и горную местность.

Для изображения рельефа на планах и картах пользуются абсолютными отметками, подписывая их у соответствующих точек плана (карты), гипсометрической или послойной окраской (чем выше, тем темнее), штрихами, омывкой, комбинированным способом, но особенно часто горизонталями, дополненными абсолютными отметками и бергштрихами. Этот способ имеет большие преимущества по сравнению с другими. Он довольно объективен, прост для исполнения, позволяет геометрически наиболее точно передать форму рельефа и отразить его особенности.

Под горизонталями понимают след от пересечения физической поверхности Земли уровенной поверхностью, поэтому горизонтали – это линии, все точки которых имеют одинаковые абсолютные высоты.

Если характерные формы рельефа нельзя отобразить горизонталями с основным сечением, то пользуются полугоризонталями с высотой сечения равной половине основного сечения. Для показа на картах микрорельефа степной или плоскоравнинной местности, кроме полугоризонталей, применяют вспомогательные горизонтали с такой высотой сечения, которая позволяет нагляднее передать эти элементы рельефа.

Горизонтали вы также видели на картах при выполнении контрольной работы. Основные горизонтали изображаются сплошными линиями, полугоризонтали – штрихом.

Чтобы иметь возможность соединить отдельные топографические карты и планы, счет горизонталей ведут от основной уровенной поверхности.

1.7 Содержание карт и планов

Для определения географических или прямоугольных координат точек на топографической карте пользуются координатной сеткой и градусной рамкой. Внутренняя рамка, т.е. рамка, ограничивающая картографический материал, на топографических картах представляет собой трапецию, в углах которой подписаны координаты – широта и долгота.

Между внешней (оформительской) и внутренней рамкой помещена минутная рамка, позволяющая определять географические координаты точек. На листах карты нанесена координатная сетка, линии которой параллельны осям координат (линиям осевого меридиана и экватора). Координатная сетка подписана и позволяет определять прямоугольные геодезические координаты точек. Размер стороны квадрата координатной сетки соответствует 1 км в масштабе данной карты.

Над верхней рамкой карты указывается номенклатуру листа, название наиболее значительного населенного пункта и систему координат карты. Под нижней рамкой приводят данные о склонении магнитной стрелки, сближении меридианов, схему взаимного положения вертикальной линии сетки и истинного и магнитного меридианов, численный и линейный масштабы, график заложения и указывается год издания карты.

Важнейшим показателем топографических и лесных планов и карт является их наглядность. Она достигается применением соответствующих условных знаков. Все условные знаки делятся на общетопографические и специальные. Общетопографические условные знаки в свою очередь подразделяются на внемасштабные, знаки для объектов линейного протяжения и контурные.

Внемасштабными условными знаками изображают малые по площади объекты, контуры которых не выражаются в масштабе плана или карты.

Объекты линейного протяжения на местности, такие как границы, дорожная сеть, реки и т.п., обозначаются на планах (картах) линейными условными знаками.

Контурными (площадными) или масштабными, условными знаками показывают в масштабе карты (плана) объекты местности с отображением действительных их размеров и формы.

Специальные условные знаки применяют, например, для планшетов, планов лесонасаждений и схематических карт лесхозов.

ТЕМА 3 Обозначение, измерение

и ориентирование линий на местности

Определение дирекционного угла заданной на карте линии,

вычисление ее истинных и магнитных азимутов и румбов

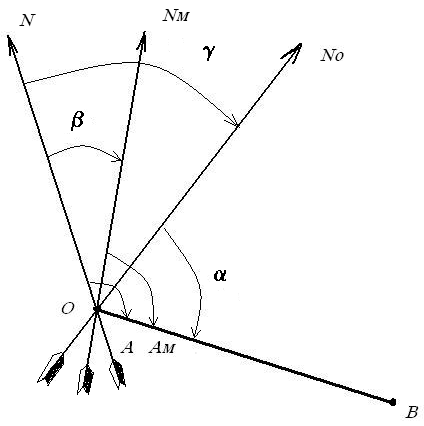
Ориентированием линии на местности называется определение ее направление относительно какого-либо другого направления, принимаемого за начальное. За начальные принимаются направления (рис.): N - истинного (географического) меридиана, Nм - магнитного меридиана либо No - осевого меридиана зоны, т. е. оси Ох или линии, ей параллельной.

Nм – магнитным азимутом (А^М); от осевого меридиана Nо (или оси абсцисс X) – дирекционным углом (α). Направление истинного меридиана определяется с помощью астрономических наблюдений, магнитного – с помощью магнитной стрелки (компаса, буссоли). Азимуты и дирекционные углы могут иметь значения от 0⁰ до 360⁰, а румбы - от 0⁰ до 90⁰ с указанием названия четверти.

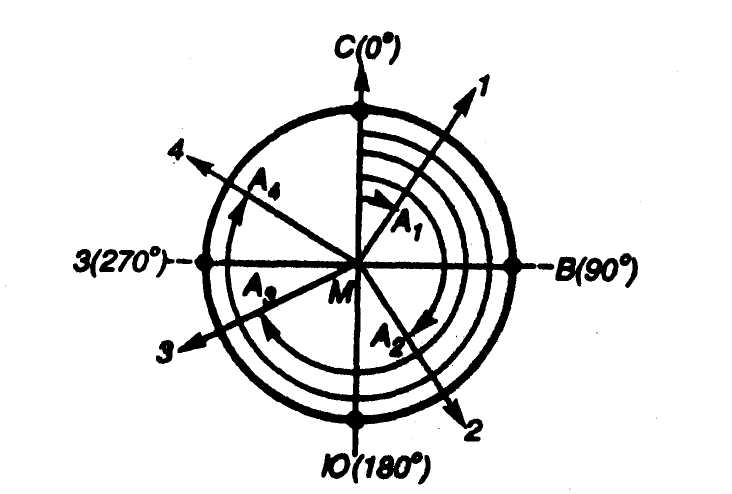
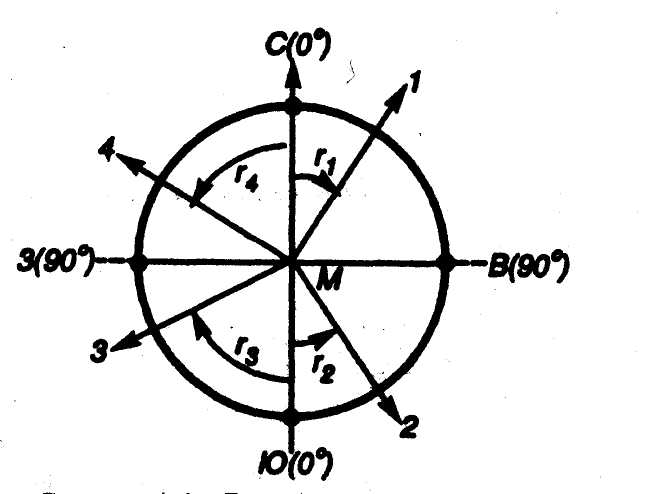
Румбом (r₁, r₂, r₃, r₄) называют острый горизонтальный угол, отсчитываемый от ближайшего направления меридиана (северного или южного)

до данной линии (рис. 10). Румбы, как и азимуты, могут быть истинными и магнитными. Существует связь между азимутами и румбами (табл.2).

Таблица

Связь азимутов и румбов

Дирекционным углом () называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана или линии ему параллельной (на плане это вертикальные линии координатной сетки) по ходу часовой стрелки до направления данной линии.

Измерение дирекционного угла заданной на карте линии производят с помощью транспортира. Для этого продолжают ориентируемую линию до пересечения с ближайшей линией координатной сетки, параллельной оси ОХ, совмещают центр транспортира с полученной точкой пересечения, а нулевой диаметр транспортира совмещают с положительным направлением оси ОХ.

Для каждой линии различают прямое и обратное направление. Дирекционные углы (как и азимуты) _пр прямого и _обр обратного направления отличаются на 180⁰: _пр=_обр180⁰.

Магнитный меридиан, как правило, не совпадает с истинным в данной точке земной поверхности, образуя с ним некоторый угол δ, называемый склонением магнитной стрелки (рис.). Угол δ отсчитывается от истинного меридиана до магнитного и может быть восточным (со знаком плюс) и западным (со знаком минус). Зная склонение магнитной стрелки в данной точке, можно осуществить переход от магнитного азимута направления к истинному по формуле: А = А_м + δ

Угол γ, на который линия координатной сетки, параллельная оси ОХ, отклоняется от истинного меридиана данной точки (вследствие сферичности Земли), называется сближением меридианов (рис.). Как и склонение сближение может быть восточным (положительным) или западным (отрицательным).

Сведения о величинах сближения меридиан и магнитного склонения, а также схема взаимного расположения истинного, магнитного и осевого меридианов приводится в зарамочном оформлении карты в левом нижнем углу.

Измерив дирекционный угол α заданной на карте линии, вычисляют ее истинный и магнитный азимуты по формулам:

А = α + γ, А^М = α + γ – δ.

Например, по заданию α_АВ=102⁰, γ=2⁰11^/- восточное, δ=1⁰54^/- западное;

Тогда, если _пр=_обр180⁰, то _ВА=_АВ+180⁰=102⁰+180⁰=282⁰;

азимуты: А= α +(+γ)=102⁰+(+2⁰11^/)=102⁰+2⁰11^/=104⁰11^/;

А_М = α + (+γ) –(- δ)=102⁰+(+2⁰11^/)-(-1⁰54^/)=102⁰+2⁰11^/+1⁰54^/)=

=105⁰+65^/=106⁰05^/;

румбы: r (ЮЗ, т.к.90⁰104⁰11^/(А)180⁰ вторая четверть)= 180⁰ -A =

=180⁰-104⁰11^/= 179⁰60^/-104⁰11^/=75⁰49^/;

r_м (ЮЗ, т.к.90⁰106⁰05^/(А_м)180⁰ вторая четверть)= 180⁰ –A_м =

=180⁰-106⁰05^/= 179⁰60^/-106⁰05^/=73⁰55^/.

Тема 4, 5 и 7 (см метод.Указание по теодолитно-тахеометрической съемке по летней практике)

Тема 4 Угломерные инструменты и их применение

При геодезических работах широко применяются приборы для измерения горизонтальных и вертикальных углов любой величины.

Когда требуется измерить угол на точке местности, то обычно два пункта визирования не находятся в горизонтальной плоскости, проходящей через точку стояния прибора. В геодезии же используются горизонтальные углы, представляющие собой проекции углов местности на горизонтальную плоскость.

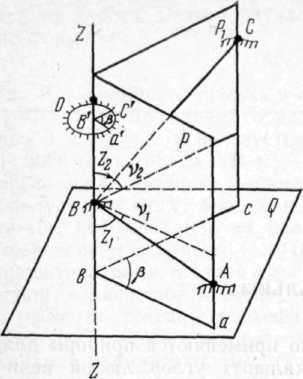
Изложенный геометрический принцип измерения горизонтального угла осуществляется в угломерном приборе - теодолите.

Вертикальные углы направлений на точку визирования лежат в вертикальной плоскости. Если вертикальные углы отсчитываются от отвесной оси ZZ до направлений на точки А и С , то углы Z₁ и Z₂ называются зенитными расстояниями. При отсчете вертикальных углов от горизонтальных проекций линий до их направлений получают углы наклона υ₁ и υ_2.

Классификация теодолитов

Существующие типы теодолитов различаются по точности, виду отсчетных устройств, конструкции системы вертикальных осей горизонтального круга и назначению.

В зависимости от точности измерения горизонтальных углов в соответствии с ГОСТ 10529 - 86 теодолиты могут быть разделены на 3 типа:

1. Высокоточные Т1, предназначенные для измерения углов триангуляции и полигонометрии 1 и 2 классов.

2. Точные Т2 - для измерения углов в триангуляции и полигонометрии 3 и 4 классов; Т5 - для измерения углов в триангуляционных сетях и полигонометрии 1 и 2 разрядов.

3. Технические Т15, ТЗО и Т60 - для измерения углов в теодолитных и тахеометрических ходах и съемочных сетях.

В условных обозначениях теодолитов цифра означает среднюю квадратическую погрешность измерения горизонтального угла одним приемом в секундах; для теодолита Т5 m_β = 5", для Т3О m_β = 30" и т. д.

Теодолиты со стеклянными угломерными кругами и оптическими отсчетными устройствами называются оптическими; в них с помощью оптической системы изображения горизонтального и вертикального кругов передаются в поле зрения специального микроскопа. В настоящее время отечественной промышленностью выпускаются только оптические теодолиты.

Теодолит т-30, 2т-30

Теодолит - геодезический прибор, предназначенный для измерения и построения горизонтальных и вертикальных углов, определения магнитных азимутов и расстояний.

Устройство теодолита

Общий вид теодолита технической точности Т-30 показан на рис. Теодолит состоит из следующих основных узлов:

1 - подставка теодолита,

2 - подъемные винты,

3 - горизонтальный круг ГК (лимб и алидада),

4 - подставка зрительной трубы,

5 - зрительная труба,

6 - кремальера (фокусировочный винт зрительной трубы),

7 - оптический визир,

8 - вертикальный круг (ВК),

9 - цилиндрический уровень,

10 - зеркало подсветки,

11 - штриховой микроскоп.

Для перемещения, закрепления и точного наведения прибора служат следующие винты:

12 - зажимной винт лимба горизонтального круга (ГК),

13 - наводящий (микрометренный) винт лимба горизонтального круга (ГК),

14 - зажимной винт алидады,

15 - наводящий (микрометренный) винт алидады,

16 - зажимной винт зрительной трубы,

17 - наводящий (микрометренный) винт зрительной трубы.

Теодолит устанавливается на штативе и закрепляется становым винтом. В теодолите различают следующие главные оси:

VV₁ - ось вращения прибора,

LL₁ - ось цилиндрического уровня,

TT₁ - ось вращения зрительной трубы,

KK₁ - визирная ось зрительной трубы.

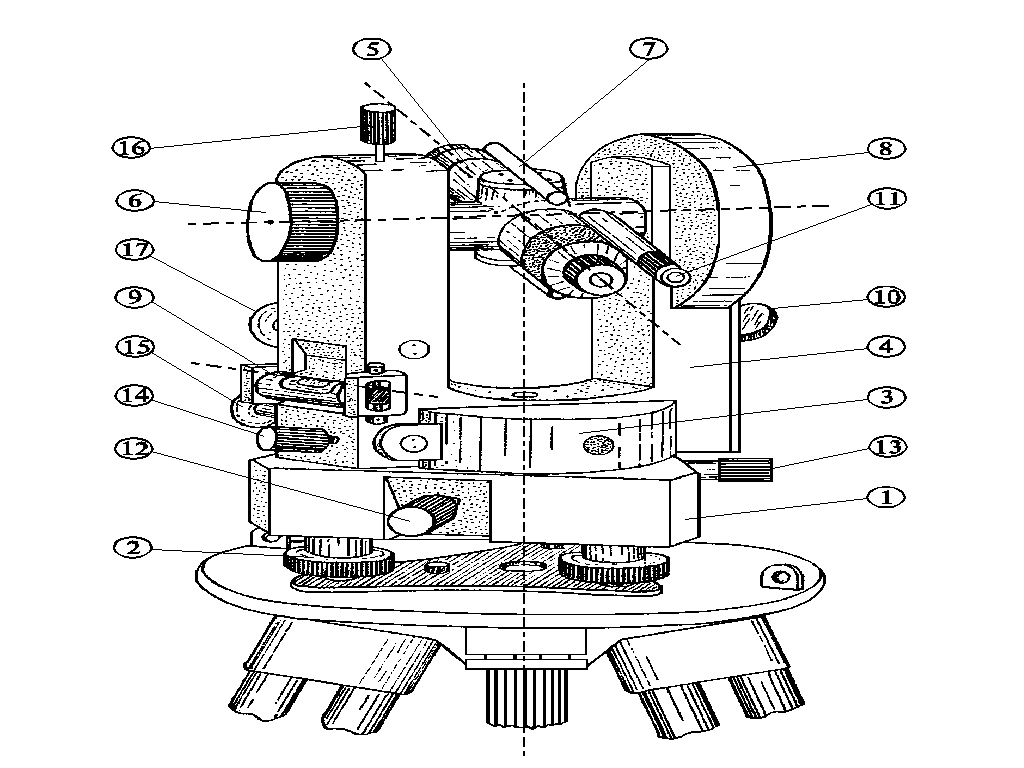
Рис.

В теодолите различают два положения прибора. В случае, когда вертикальный круг находится справа от зрительной трубы (со стороны окуляра) ,то такое положение теодолита называют круг право (КП). Положение теодолита, когда вертикальный круг находится слева, называют кругом лево (КЛ). Для того чтобы поменять положение теодолита необходимо перевести зрительную трубу через зенит на 180º.

Цилиндрический уровень - служит для нивелирования прибора, т.е. для приведения плоскости лимба горизонтального круга в горизонтальное положение (или оси вращения прибора VV₁ в отвесное положение).

Он представляет собой стеклянную ампулу 1, внутренняя поверхность которой в продольном сечении имеет сферическую поверхность. Ампулу заполняют эфиром в нагретом состоянии, после чего запаивают. При охлаждении пары эфира образуют пузырек (2). На внешней поверхности ампулы нанесены штрихи. Средняя точка на шкале (3) называется нульпунктом уровня. Осью цилиндрического уровня (LL₁) называют линию, касательную к внутренней поверхности цилиндрического уровня в нульпункте. Ось уровня занимает горизонтальное положение, если пузырек находится в нульпункте. Цилиндрический уровень имеет исправительные винты, которые служат для юстировки уровня.

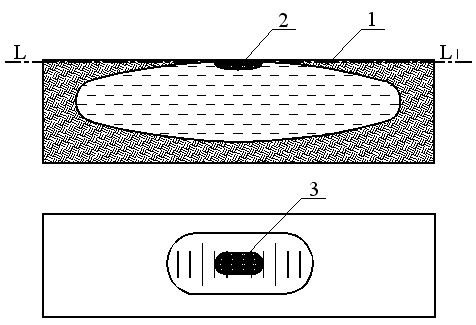
Порядок нивелирования теодолита:

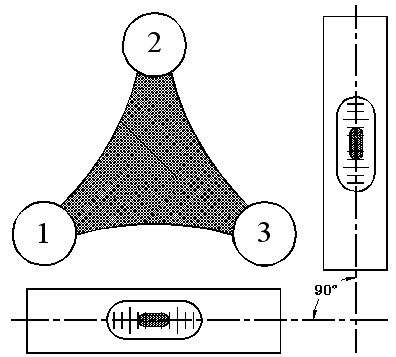
- открепляют зажимной винт алидады и устанавливают уровень параллельно двум подъемным винтам (1 и 3, ),

- вращая эти винты одновременно в противоположные стороны, выводят, пузырек уровня в нульпункт,

- поворачивают алидаду с уровнем на 90⁰ и вновь выводят пузырек уровня в нульпункт, действуя третьим подъемным винтом.

Эти действия повторяют до тех пор, пока пузырек не будет оставаться в нульпункте при любом повороте теодолита вокруг его оси

Допускается отклонение не более одного деления.

Зрительная труба - предназначена для визирования на точки местности. Зрительная труба состоит из объектива (1),окуляра (2) и визира (3). Оптическая система зрительной трубы дает увеличенное (20^х) и обратное изображение наблюдаемого предмета, Зрительная труба имеет внутреннюю фокусировку. Для получения четкого изображения наблюдаемого предмета служит кремальера. Для непосредственного визирования на точки местности служит сетка нитей, которая видна в поле зрения зрительной трубы. Сетка нитей представляет собой стеклянную пластинку с нанесенными вертикальными и горизонтальными штрихами. Сетка нитей имеет исправительные (юстировочные) винты. Для получения четкого изображения сетки нитей служит диоптрийное кольцо (4)

Визирной осью зрительной трубы (КК₁) называют воображаемую линию, соединяющую центр сетки нитей с оптическим центром объектива. Продолжение визирной оси до наблюдаемого предмета называют визирным лучом.

Визировать на точку значит, наблюдая в зрительную трубу, совместить центр сетки нитей с изображением наблюдаемой точки.

Порядок визирования:

- фокусируют изображение сетки нитей,

- закрепляют лимб горизонтального круга,

- открепляют зажимные винты алидады и зрительной трубы,

- наводят крест визира на заданную точку,

- закрепляют алидаду и зрительную трубу,

- фокусируют изображение наблюдаемой точки (рис.),

- совмещают центр сетки нитей с наблюдаемой точкой, вращая наводящие винты алидады и зрительной трубы.

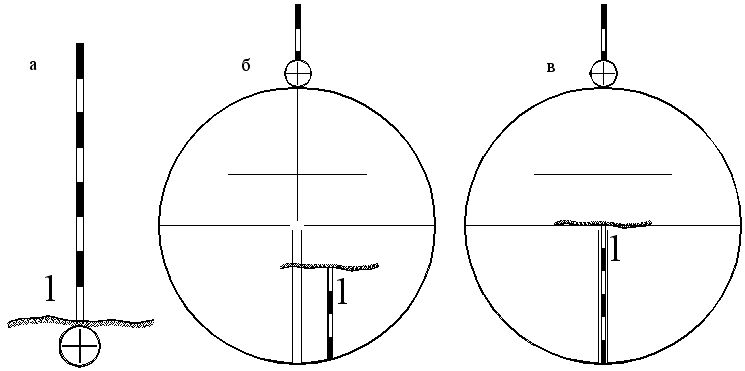
Рис.

В результате визирования изображение точки должно находиться в центре сетки нитей, причем изображение сетки нитей и наблюдаемой точки должно быть четким.

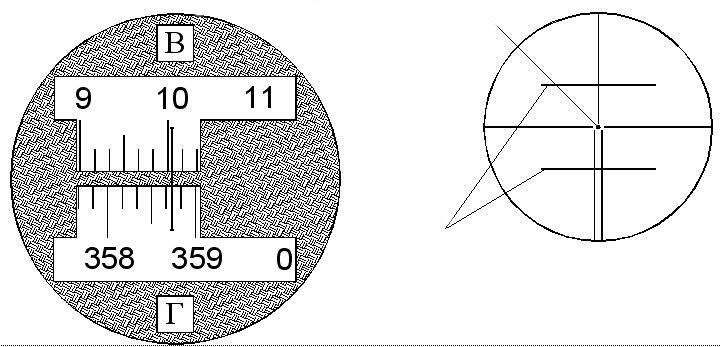
Штриховой микроскоп - служит для взятия отсчетов по лимбам горизонтального и вертикального кругов. Лимбы горизонтального и вертикального кругов представляют собой диски, на которых нанесены шкалы с ценой деления 10' и подписано каждое градусное деление. Деления возрастают по ходу часовой стрелки, а в поле зрения штрихового микроскопа - слева направо.

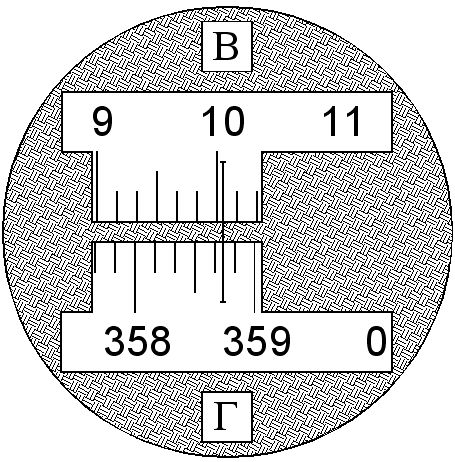
Изображения делений горизонтального (1) и вертикального (2) кругов с помощью оптической системы передается в поле зрения микроскопа (рис.). Освещение лимбов ГК и ВК производится лучом света, отраженным от зеркала подсветки, Четкость изображения делений лимбов регулируют вращением диоптрийного кольца на окуляре микроскопа.

Отсчет производят по неподвижному штриху-индексу. Отсчет берут с точностью до 1'. Например, на рис. отсчет по лимбу горизонтального круга равен 358º 43' , а отсчет по вертикальному кругу равен 9º 57'.

Поверки теодолита

Для получения правильных результатов измерений в теодолите должны соблюдаться определенные геометрические условия. Выполнение этих условий выявляют в результате поверки прибора. Если выясняется, что геометрическое условие не выполняется, то производят исправление (регулировку прибора). Для теодолита Т30 проверяют выполнение следующих условий:

I условие. Ось цилиндрического уровня должна быть перпендикулярна к оси вращения прибора.

LL_{1 ┴} VV₁

Порядок выполнения:

- теодолит закрепляют на штативе, нивелируют и закрепляют лимб горизонтального круга,

- устанавливают уровень параллельно двум подъемным винтам, например, 1 и 3 (рис.) и закрепляют алидаду,

- вращая указанные подъемные винты одновременно в противоположные стороны, выводят пузырек уровня в нульпункт,

- открепляют алидаду, поворачивают ее вместе с уровнем на 180⁰

Считают, что условие LL_{1 ┴} VV₁ выполнено, если пузырек остается в нульпункте или отклоняется от него не более чем на одно деление

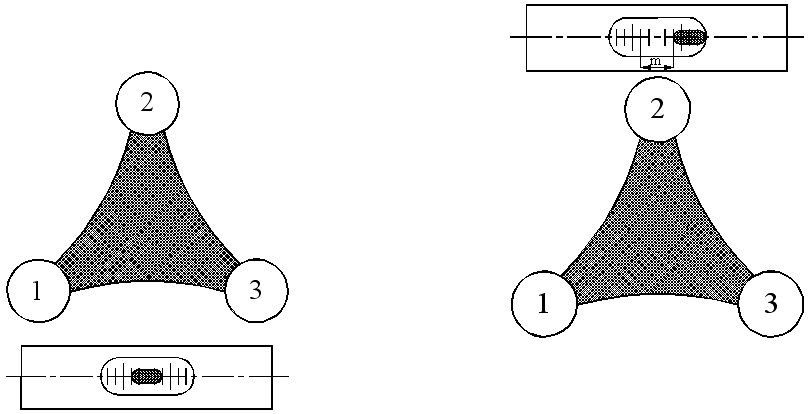
Рис.

Если пузырек ушел из нульпункта на m (m > 1) делений , то условие не выполнено и цилиндрический уровень необходимо исправить.

Порядок исправления цилиндрического уровня:

- возвращают пузырек к нульпункту на половину отклонения (m/2) с помощью исправительных винтов уровня и шпильки,

- выводят пузырек уровня окончательно в нульпункт с помощью подъемных винтов (1 и 3).

Действия, указанные выше, повторяют до тех пор, пока не будет выполняться условие m ≤ 1.

II условие. Визирная ось зрительной трубы должна быть перпендикулярна к оси вращения зрительной трубы.

KK_{1 ┴} TT₁

Коллимационной плоскостью называют плоскость, образуемую при вращении зрительной трубы вокруг ее оси ТТ₁. В случае выполнения условия коллимационная плоскость _┴ оси вращения зрительной трубы.

Коллимационной ошибкой называют угол между визирной осью зрительной трубы и перпендикуляром к оси вращения зрительной трубы.

Коллимационную ошибку (с) вычисляют по формуле:

где: О_КЛ и О_КП - отсчеты по лимбу горизонтального круга.

Условие считается выполненным, если:

| c | ≤ 1.5t,

где: t - точность взятия отсчета по лимбу горизонтального круга.

Для теодолита Т-30 | с | < 2’.

Проверка выполнения II условия сводится к определению коллимационной ошибки зрительной трубы теодолита и, если ошибка превышает допустимую, то ее исправляют.

Порядок определения коллимационной ошибки:

- закрепляют лимб горизонтального круга,

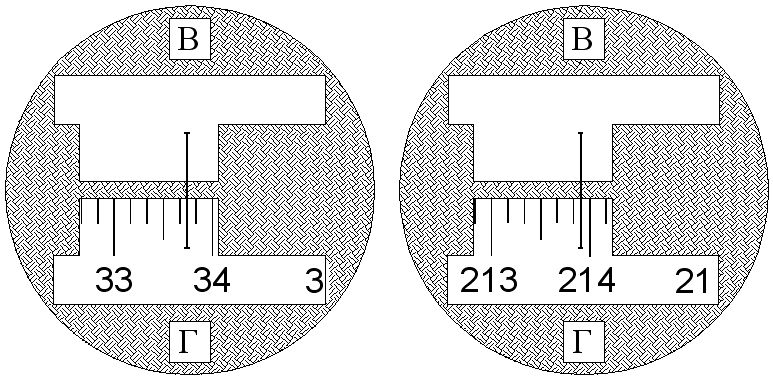
Рис.

- выбирают удаленную, неподвижную и хорошо видимую точку местности (на рис., а это низ вехи),

- визируют при КЛ на выбранную точку и берут отсчет по лимбу горизонтального круга, например: О_кл = 33^о 44^’

- переводят зрительную трубу через зенит и визируют на ту же точку местности при КП, берут отсчет по лимбу горизонтального круга.

например: О_кп = 213º 54' ,

- вычисляют коллимационную ошибку:

Полученная коллимационная ошибка является недопустимой и ее необходимо исправить.

Порядок исправления коллимационной ошибки:

- вычисляют исправленный отсчет:

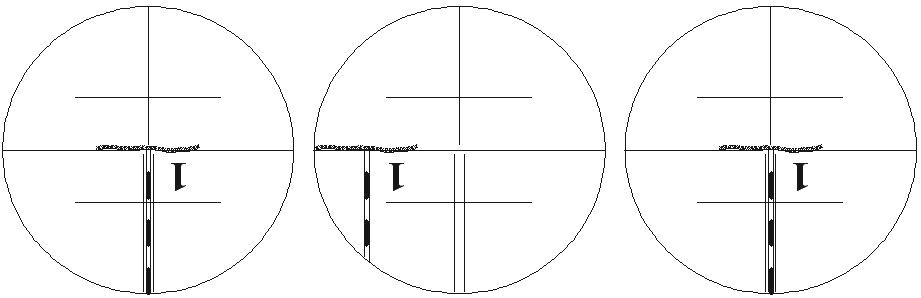
Рис.

Например:

- устанавливают исправленный отсчет на лимбе горизонтального круга, вращая наводящий винт алидады, при этом наблюдаемая точка уйдет из центра сетки нитей (рис.),

- возвращают центр сетки нитей к наблюдаемой точке, вращая шпилькой боковые исправительные винты сетки нитей (рис.).

В результате исправления мы снова видим наблюдаемую точку в центре сетки нитей, а отсчет по лимбу горизонтального круга равен исправленному отсчету. После исправления рекомендуется повторно определить коллимационную ошибку.

III Условие. Вертикальная нить сетки нитей должна быть отвесна.

Порядок выполнения:

- подвешивают отвес на расстоянии примерно 10 м от теодолита,

- визируют на нить отвеса и совмещают вертикальную нить сетки нитей с нитью отвеса.

Если эти нити совпадают (или параллельны), то условие выполнено (рис.).

Если нити пересекаются (рис.), то условие не выполнено и необходимо исправить сетку нитей.

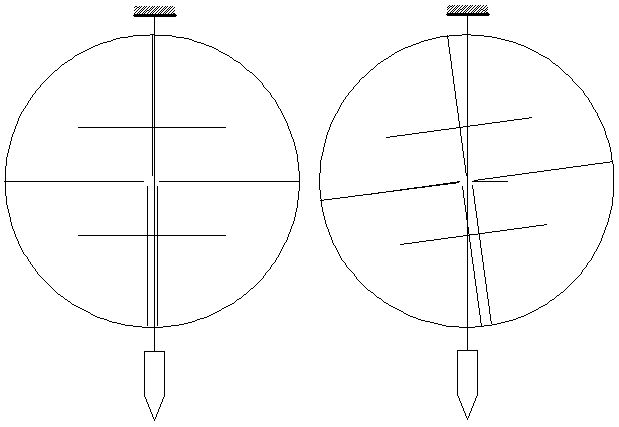
Порядок исправления:

- открепляют крепежные винты сетки нитей и поворачивают окулярное колено с сеткой нитей до тех пор, пока вертикальная нить сетки нитей не совпадет с нитью отвеса,

- винты закрепляют и снова определяют выполнение III условия.

Если производился поворот сетки нитей, то после этого необходимо снова определить коллимационную ошибку зрительной трубы.

IV условие. Место нуля вертикального круга теодолита должно быть близко к нулю.

Место нуля вертикального круга (МО) - отсчет по вертикальному кругу, когда визирная ось зрительной трубы горизонтальна, а пузырек цилиндрического уровня находится в нульпункте.

Место нуля определяют по формуле:

где: О_КЛ и О_КП - отсчеты по вертикальному кругу теодолита.

Примечание: если О_КЛ < 90º, то к нему прибавляют 360º.

Если МО отличается от нуля больше, чем на 2', т.е. находится в пределах

359º58' ≤ МО ≤ 360º 02' , то МО исправляют, т.е. приводят к нулю.

Порядок определения МО:

- нивелируют теодолит,

- визируют при КП на удаленную, хорошо видимую точку местности и берут отсчет по лимбу вертикального круга.

Например: О_КП = 170^о 03^о, (рис.)

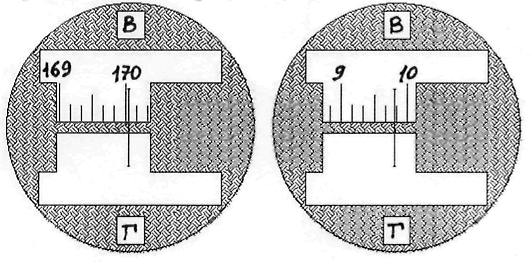
Рис.

Примечание: перед тем как взять отсчет необходимо следить, чтобы пузырек уровня находился в нульпункте и при необходимости выводить его в нульпункт подьемными винтами теодолита,

- переводят зрительную трубу через зенит,визируют на ту же точку при КЛ и берут отсчет по лимбу вертикального круга.

Например: О_КЛ = 9^о 49’ ,(рис.),

- вычисляют МО вертикального круга теодолита:

Полученное МО отличается от нуля больше, чем на 2’ поэтому его необходимо исправить.

Порядок исправления МО:

- вычисляют исправленный отсчет:

- устанавливают исправленный отсчет на лимбе ВК, вращая наводящий винт зрительной трубы, при этом наблюдаемая точка уйдет из центра сетки нитей (рис.),

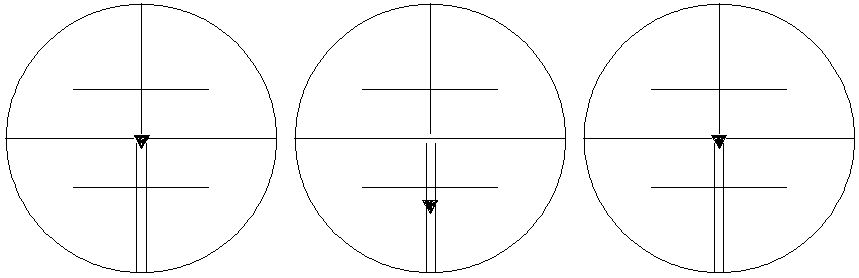
Рис.

- совмещают центр сетки нитей с наблюдаемой точкой, вращая шпилькой вертикальные исправительные винты сетки нитей (рис.)

После исправления рекомендуется повторно определить МО и снова проверить выполнение II и III условий.

Измерение горизонтальных углов

(Способ приемов)

Порядок измерения угла теодолитом т30.

1. Устанавливают теодолит в рабочее положение.

– центрируют теодолит с помощью отвеса над вершиной измеряемого угла (точка 2) с точностью 3 – 5 мм; нивелируют прибор с помощью цилиндрического уровня.

2. Фокусируют изображение сетки нитей с помощью диоптрийного кольца окуляра зрительной трубы.

3. Фиксируют положение лимба закрепительным винтом лимба (10),

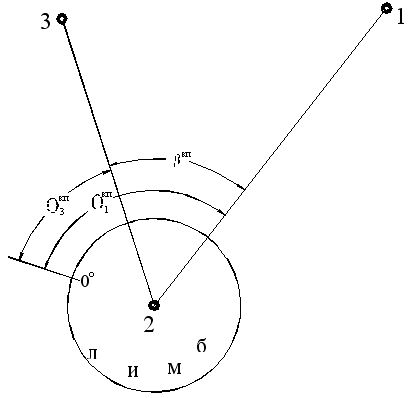
Рис.

3.При положении теодолита КП визируют центр сетки нитей на заднюю (правую) точку (точка 1) и берут отсчет О₁^КП по лимбу горизонтального круга, который записывают в графу 4 журнала измерения углов; например: О₁^КП=193º 16'.

4. Открепляют зажимные винты алидады и трубы и визируют на переднюю (левую) точку (точка 3) и берут отсчет О₃^КП по лимбу горизонтального круга, который записывают в графу 4 журнала измерения углов; например: О₃^КП=151º 51'.

5. Вычисляют значение угла β^кп , измеренного при КП.

β^кп = О₁^КП - О₃^КП

Пример:

β^кп = 193º 16' - 151º 51' = 41º 25'

Результат записывают в графу 5 журнала

Теодолит Т30 № 25 097

Дата 26.02.04 г. Погода Ясно

6. Переводят трубу через зенит, т.е. устанавливают положение теодолита КЛ.

7. Измеряют угол при КЛ, повторяя действия пунктов 3, 4 и выполняя соответствующие записи в журнале (графа 4).

Например: О₁^КЛ = 13º 18' и О₃^КЛ = 331º 51'.

8. Вычисляют значение горизонтального угла, измеренного при КЛ:

β ^КЛ = О₁^КЛ - О₃^КЛ

Пример:

β ^КЛ = (13º 18' + 360º00') - 331º 51' = 41º 27'

В примере О₁^КЛ < О₃^КЛ , поэтому к первому отсчету прибавляют 360º. Результат записывают в графу 5 журнала.

Производят контроль измерения горизонтального угла:

|β^КЛ - β^КП | ≤ 2'

Пример:

41º27 - 41º 25' = 2'

Результат записывают в графу 6 журнала.

9. Если условие выполняется, то вычисляют среднее значение измеренного угла:

Измерение вертикальных углов

Вертикальный угол или угол наклона - это угол, отсчитываемый в вертикальной плоскости до наблюдаемого направления выше горизонта (со знаком “+“) или ниже горизонта (со знаком “ – “).

Лимб вертикального круга закреплен на оси вращения зрительной трубы и вращается вместе с ней. Отсчеты берутся по отсчетному микроскопу (по верхней части поля зрения, индекс “B”).

Порядок измерения вертикального угла.

При двух положениях круга трубу визируют на данную точку и берут отсчеты по вертикальному кругу, Перед отсчитыванием пузырек уровня выводят в нуль пункт (подъемными винтами теодолита Т-30). По полученным отсчетам вычисляют место нуля вертикального круга (МО), а затем вычисляют угол наклона.

Угол наклона вычисляют по формулам (для Т-30):

ν = КЛ -МО

В необходимых случаях к малым отсчетам КЛ или МО также прибавляют 360°. Например, КП = 170°36', КЛ = 9°20'

ν = 9˚20΄ + 360˚ 00΄ -359˚ 59΄ = 9˚ 21΄

Контролем измерения вертикальных углов служит постоянство места нуля в пределах ±2΄, а также сходимость по величине в пределах 2΄ прямого и обратного углов наклона одной и той же линии. Знаки углов - противоположные.

Буссоли и гониометр

В работах по лесоустройству находят применение буссоли и гониометры. Буссоль может быть самостоятельным прибором или дополнительным приспособлением к более сложному угломерному устройству, например к теодолиту.

Устройство буссолей. Буссоль Б С - 2. Буссоль БС-2 (буссоль Стефана) состоит из следующих основных частей (рис. VI.23): собственно буссоли 1, алидады 6, лимба 7 и втулки 8. Втулка служит для закрепления буссоли на головке штатива или на верхнем конце деревянного стержня. Лимб жестко соединен с буссолью, и обе эти части могут совместно вращаться по втулке. В коробке буссоли имеется градусное кольцо 4.

Примечание. Если на градусном кольце буссоли деления подписаны от 0 до 360°, то такое кольцо называется азимутальным. Если же противоположные деления одного из диаметров кольца отмечены подписями 0° и от каждого из них значения градусов возрастают в обе стороны до 90°, то такое кольцо называется румбшеским.

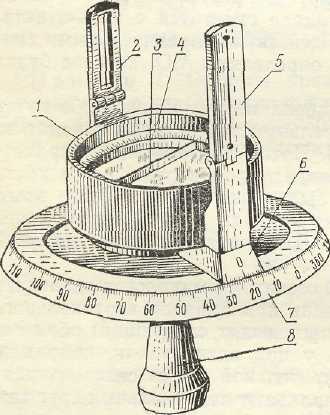
Рис. VI.23. Буссоль БС-2.

Магнитная стрелка 3 буссоли свободно подвешена на острие шпиля, укрепленного в центре градусного кольца 4. Северный конец ее окрашен в черный цвет. В нерабочем положении стрелка должна быть прижата к защитному стеклу буссоли при помощи арретирующего устройства, приводимого в действие вращением кольца крышки буссоли,

Буссоль БШ. Особенность этой буссоли состоит в соеди­нении магнитной стрелки с легким градуированным лимбом. Лимб вращается вместе со стрелкой на острие шпиля. У глазного диоптра в его нижней части расположена призма-лупа, которая облегчает оценку десятых долей градуса при отсчетах делений лимба, нанесенных через 1°. Буссоль БШ устанавливают на штатив или кол. Этой буссолью можно пользоваться, удерживая ее в руке.

Поверки буссоли.

Буссоль должна удовлетворять следующим условиям.

1. Магнитная стрелка должна быть уравновешена. Для приведения стрелки в горизонтальное положение служит передвижная муфточка. Если муфточки нет, стрелку можно уравновесить кусочками воска, алюминиевой фольги и т. д.

2. Магнитная стрелка должна обладать достаточной чувствительностью. Для поверки этого условия по одному из концов свободно установившейся на шпиле стрелки производят отсчет делений кольца буссоли, затем с помощью магнита выводят стрелку из состояния покоя, после чего магнит убирают. Хорошо намагниченная стрелка возвращается на прежний отсчет. Если после неоднократного исполнения этой поверки обнаруживается несовпадение отсчетов, то причиной недостаточной чувствительности магнитной стрелки могут быть: слабая намагниченность стрелки, плохая шлифовка агатовой опоры в шляпке стрелки, затупление острия шпиля. Такие буссоли подлежат исправлению.

3. Буссоль не должна содержать намагничиваемых деталей, влияющих на отклонение стрелки (кроме шпиля и стрелки). Это условие обеспечивается заводом. Поверку делают во время приемки буссоли после ремонта. Для этого снимают стрелку, вы­винчивают шпиль и вставляют его вертикально в доску, стрелку вешают на шпиль. К успокоившейся стрелке подносят корпус поверяемой буссоли. Если стрелка остается неподвижной, то условие выполняется.

4. Ось вращения магнитной стрелки должна совпадать с центром градусного кольца, в противном случае стрелка будет иметь эксцентриситет. Условие считается выполненным, если отсчеты по противоположным концам стрелки отличаются на 180°. Для поверки этого условия буссоль поворачивают через каждые 30—40° и производят отсчеты по обоим ее концам. Буссолью, у которой стрелка имеет эксцентриситет, работать можно, но при этом отсчеты следует производить по обоим концам стрелки. Среднее значение из этих отсчетов будет свободно от погрешности, обусловленной эксцентриситетом. Например, если отсчет по северному концу стрелки a_I = 30,5°, а по южному а₂—211,3°, то средний отсчет по северному концу а —30,9°.

5. Магнитная и геометрические оси стрелки должны совпадать. Для поверки этого условия снимают защитное стекло буссоли и производят отсчет по северному концу стрелки. Затем снимают стрелку со шпиля, перевинчивают шляпку на другую сторону стрелки и, установив стрелку на шпиль, снова берут отсчет по тому же ее концу. Разность отсчетов будет равна двойному углу между указанными осями стрелки. Если погрешность заметна, то ее учитывают при определении магнитных азимутов или румбов введением соответствующих поправок в отсчеты.

Эту поверку можно выполнить также сравнением показаний стрелок поверяемой и исправной буссолей.

6. Коллимационная плоскость диоптров должна быть перпен­дикулярна к плоскости градусного кольца буссоли и проходить через его нулевой диаметр. Для поверки этого условия плоскость кольца буссоли с помощью выверенного уровня устанавливают в горизонтальное положение. В 10—15 м от буссоли вешают шнур с отвесом и визируют на него через диоптры. Если волосок предметного диоптра закрывает шпур отвеса на всем своем протяжении, т. е. при совпадении коллимационной плоскости со шнуром > значит диоптры установлены правильно.

Положение нулевого диаметра градусного кольца проверяют линеечкой, совместив ее ребро с противоположными штрихами этого диаметра. Вдоль ребра линеечки визируют на шнур отвеса, и если при этом линия визирования, проходящая через глазной и предметный диоптры, совпадает со шнуром отвеса, то условие выполнено. В противном случае кольцо буссоли следует повернуть на соответствующий угол.

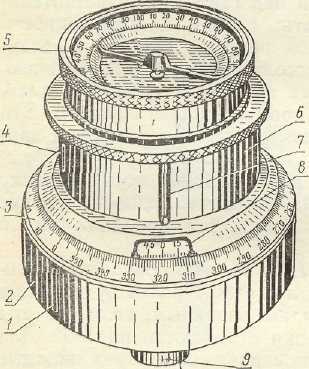
Рис. V1.24. Гониометр.

Для приведения гониометра в отвесное положение рекомендуется применять накладной круглый уровень.

Поверки гониометра. Гониометр должен удовлетворять сле­дующим геометрическим условиям.

1. Ось вращения верхнего цилиндра должна совпадать с осью нижнего цилиндра. Для поверки этого условия берут отсчеты по двум верньерам через каждые 20—30° делений лимба. В исправном приборе отсчеты по противоположным верньерам должны отличаться не более чем на 180±tf (где t=b' — точность верньера).

2. Нулевой диаметр верньеров при совмещении плоскостей, проходящих через пару соответствующих верхних и нижних диоптров, должен совпадать с нулевым диаметром лимба (0—180°). Для поверки этого условия гониометр устанавливают на штативе по уровню и, вращая по азимуту, визируют через нижние диоптры на находящуюся на местности веху. Затем, сохраняя нижний цилиндр неподвижным, вращают верхний цилиндр и визируют через верхние диоптры на ту же веху. Если поверяемое условие выполнено, то отсчеты по первому и по второму верньерам будут соответственно 0 и 180°. При невыполнении этого условия будет иметь место коллимационная погрешность, абсолютное значение которой равно отсчету по первому верньеру. Коллимационную погрешность не исправляют, а учитывают при измерении горизонтальных углов.

3. Поверки буссоли гониометра выполняют так же, как поверки буссолей БС-2.

Тема 5 Теодолитная съемка прямая и обратная геодезические задачи.

При вычислительной обработке результатов измерений на местности, связанной с составлением плана, при проектировании участков и объектов, перед перенесением проекта в натуру возникает необходимость решать прямую и обратную геодезические задачи.

Прямая геодезическая задача состоит в том, что по координатам одного конца А: X_А и Yа линии АВ, по дирекционному углу этой линии α_АВ и ее горизонтальному проложению d_AB вычисляют координаты другого конца В этой линии: X_в, Y_в. То есть известно: X_А, Y_А, α_Аb, d_ab; вычислить X_в, Y_в. На рис.4.3 приведен наиболее простой случай, когда линия АВ расположена в первой четверти прямоугольной системы координат и имеет северо-восточное направление, когда дирекционный угол линии равен величине румба. Этот рисунок показывает, что:

X_b = X_a + (X_b - X_a)

Y_b = Y_a + (Y_b - Y_a)

З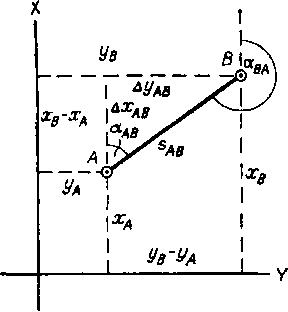 десь разности координат последующей и предыдущей точек линии называются приращениями координат этой линии. Вместе с этим (Рис.4.3) показывает, что приращениями координат линии называются ортогональные проекции горизонтального приложения этой ли-нии на оси координат. Они обычно имеют обозначение ΔX и ΔY, поэтому равенства перепишем так:

X_b = X_a + ΔX

Y_b = Y_a + ΔY

Эти равенства читают так: координата точки последующей равна координате данной точки плюс соответствующее приращение.

Далее рис. показывает, что приращения координат могут быть вычислены по дирекционному углу линии и ее горизонтальному проложению, являющемуся гипотенузой прямоугольного треугольника, в котором катеты получатся по формулам:

ΔX_АВ = S_AB cos a_AB

ΔY_AB = S_AB sin a_AB

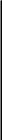Приращения координат так же, как и превышения, имеют знаки (плюс, минус). Но знаки приращений зависят от знака косинуса и синуса дирекционного угла или от названия румба линии и не зависят от четверти, образованной осями координат.

Подставив, приращения координат в вышеприведенную формулу получим формулы для решения прямой геодезической задачи

X_B = X_A + S_AB cosα_AB |

Yв=Yа+S_AB sinα_AB )

Обратная геодезическая задача состоит в том, что по координатам концов линии АВ вычисляют дирекционный угол и горизонтальное проложение этой линии. То есть известно: X_А Y_А,X_в,Y_в; вычислить α_АВ и s_AB (см. рис.4.3).

ΔX_{ав =} Xb – Xa

ΔY_{ав =} Yb – Ya

можно вычислить дирекционный угол

tgα_AB = (Y_B – Y_A) / (X_B – X_A)

Здесь особое внимание следует обратить на знаки разностей (приращений) координат Если требуется вычислять дирекционный угол α_АВ, т. е. в направлении с точки А на точку В, то, вычисляя разности, следует из координат точки последующей X_в (Y_в) вычитать координаты точки предыдущей X_А (Y_А). Эти знаки согласно табл. 5 определят название румба, а следовательно, и величину дирекционного угла.

Теперь горизонтальное проложение s_AB получится по двум формулам

S_AB = ΔX_AB/cosα_AB = (X_B – X_A) / cosα_AB

S_AB = ΔY_AB/sinα_AB = (Y_B – Y_A) / sinα_AB

cовпадение результатов, вычисляемых по этим формулам, контролирует вычисление s и α

Тема 6 Определение площадей на планах и картах

Для решения многих инженерных задач требуется знать площади участков местности. На планах и картах площади можно определить аналитическим, графическим и механическим способами.

Аналитический способ. Пусть дан четырехугольник ABCD (рис.), координаты вершин которого известны. Непосредственно из рисунка можно записать

P_ABCD =P_ABba + P_BCdb – P_CdcD – P_DcaA.

Представив площадь каждой трапеции как произведение полусуммы параллельных сторон на высоту и удвоив полученные результаты, найдем

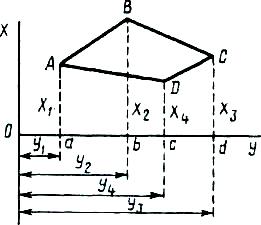
2Р = (x₁ + х₂)(y₂ – y₁) + (x₂ + x₃)(y₃ – y₂) -

- (x₃ + x₄)(y₃ – y₄) – (x₄ + x₁)(y₄ - y₁)

Преобразовывая, получим

2P = x₁(y₂ – y₄)+x₂(y₂ –y₁)+x₃(y₄ – y₂) + x₄(y₁ - y₃)

Эту формулу для случая n-угольника в общем виде можно записать

2P = Σ x_i(y _i+1 – y _i-1)

или 2P = Σ y_i(x _i-1 – x _i+1)

Точность определения площади таким способом зависит от точности определения координат точек. Если координаты точек получены по результатам измерений на местности, то точность способа повышается, так как при этом на точность вычисления площади влияют только погрешности угловых и линейных измерений на местности. Так, при измерении углов с точностью 1́́ и длин линий с точностью 1 : 2000 относительная погрешность определения площади составит примерно 1 : 1500.

Графический способ определения площадей. Для определения площадей небольших участков по плану или карте применяется графический способ с разбивкой участка на геометрические фигуры либо с помощью палеток.

В первом случае искомую площадь небольшого (до 10 - 15 см² в плане) участка разбивают на простейшие геометрические фигуры: треугольники, прямоугольники, трапеции. При криволинейном контуре участка его разбивка на геометрические фигуры выполняется с таким расчетом, чтобы стороны фигур по возможности ближе совпадали с этим контуром. Затем на плане (карте) измеряют соответствующие элементы фигур (длины оснований и высоты) и по геометрическим формулам вычисляют площади этих фигур. Площадь всего участка определяется как сумма площадей отдельных фигур.

Точность определения площади в рассматриваемом случае во многом зависит от масштаба плана (карты): чем мельче масштаб, тем грубее измеряется площадь. Поскольку графическая погрешность линейных измерений на плане (t_гр = 0,2 мм) не зависит от длины отрезков, то относительная погрешность короткой линии будет больше, чем длинной. Поэтому заданный участок следует разбивать на фигуры возможно больших размеров с примерно одинаковыми длинами оснований и высот.

Рис. Квадратная палетка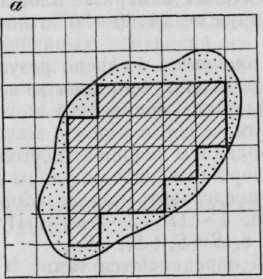

Определение площадей (до 2 - 3 см²) участков с резко выраженными криволинейными границами рекомендуется производить, с помощью квадратной палетки. Палетка представляет собой (рис.) лист прозрачной основы (целлулоида или восковки), на которую нанесена сетка квадратов со сторонами 1 - 5 мм. Зная длину сторон и масштаб плана, легко вычислить площадь квадрата палетки s.

Для определения площади участка палетку произвольно накладывают на план и подсчитывают число N₁ полных квадратов, расположенных внутри контура участка. Затем оценивают на глаз число квадратов N₂, составляемых из неполных квадратов у границ участка. Тогда общая площадь измеряемого участка

S = s (N₁+N₂)

Для контроля площадь заданного участка измеряют повторно, развернув палетку примерно на 45°. Относительная погрешность определения площади палеткой составляет 1:50—1:100.

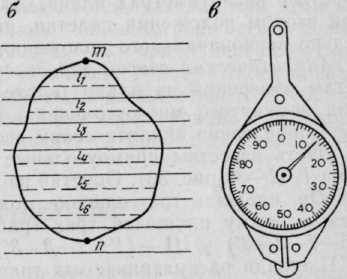
Палетка накладывается на заданный участок таким образом, чтобы крайние точки тип контура разместились посредине между параллельными линиями палетки. В результате измеряемая площадь оказывается расчлененной на фигуры, близкие к трапециям с равными высотами; при этом отрезки параллельных линий внутри контура являются средними линиями трапеции. Следовательно, для определения площади участка с помощью циркуля-измерителя и масштабной линейки нужно измерить длины средних линий трапеций l₁, l₂, ..., l_п и их сумму умножить на расстояние между линиями с учетом масштаба плана, т. е.

S = а (l₁, + l₂, + ..., + l_п ) = а Σ l_i

Суммарная длина отрезков может быть замерена с помощью курвиметра (рис.6.3 в) -прибора для измерения длин линий на плане (карте). Для этого колесо курвиметра последовательно прокатывают по измеряемым линиям и по разности начального и конечного отсчетов на циферблате определяют суммарную длину

Механический способ определения площадей. Из всех способов наиболее производительным и достаточно точным является механический способ измерения площади с помощью полярного планиметра. Имеются различные конструкции полярных планиметров. Рассмотрим одну из них двухкареточный полярный ПП-2к (рис.).

Он состоит из: двух рычагов - полюсного 1 и обводного 2, счетных механизмов 3, обводного приспособления 4. Рычаг 1 на конце имеет груз 5 с иглой, накалываемой на бумагу и служащей полюсом планиметра. Для соединения рычагов в рабочее положение штифт 6 вставляется в отверстие 7. Вспомогательными приспособлениями являются лупа 8, контрольная линейка 9 и диск 10 с иглой

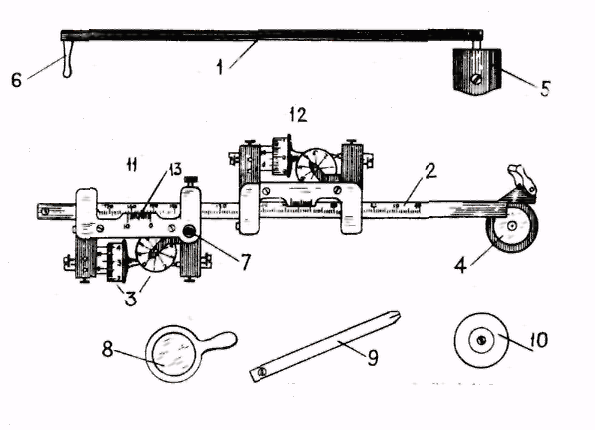
Рис.6.4

На обводном рычаге установлены две каретки: основная 11 и контрольная 12, которые могут перемещаться вдоль рычага. Основная каретка может фиксироваться, при этом по верньеру 13 отсчитывается длина рычага R с точностью 0,1мм.

Счетный механизм (рис.) состоит из счетчика оборотов 1, подвижного колесика 2 с нанесенной на него шкалой 3 из 100 делений и верньера 4.

Делением планиметра является -1/1000 длины окружности подвижного колесика, которая разделена на 100 равных частей с оцифровкой от 0 до 9. Отсчет по планиметру состоит из 4 цифр. Первая цифра (тысячи) берется по указателю 5 счетчика оборотов. Вторая (сотни) и третья (десятки) - по шкале 3 до нуля верньера (2,4 соответственно), четвертая цифра (единицы) - по номеру совпадающего штриха верньера (5). Таким образом, отсчет на рис.6.5 составляет 1245.

Для полярного планиметра различают два понятия цены деления: абсолютная и относительная.

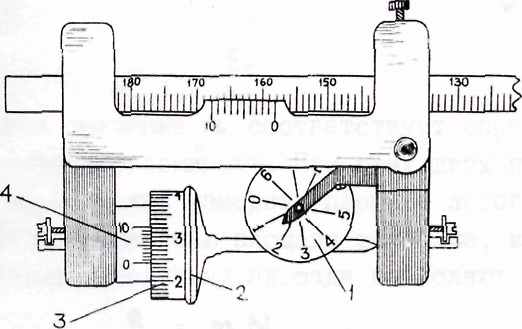
Рис 6.5

Абсолютная цена деления - это число мм² на бумаге, соответствующее одному делению планиметра.

Относительная цена деления --это число м² или га, соответствующее одному делению планиметра в масштабе данной карты. Обычно при работе с одной картой определяют относительную цену деления, которая учитывает деформацию бумаги.

Для этого на карте выбирают один или несколько квадратов километровой сетки, площадь которых вычисляют в м² или гектарах через масштаб карты (S_контр). Обводную точку совмещают с одной из вершин квадрата и на счетных механизмах берут отсчеты n1, (на основной каретке) и n¹1 (на контрольной). Обводную точку медленно перемещают по контурам квадратов в направлении хода часовой стрелки до возвращения в начальную точку. При этом необходимо, чтобы угол между рычагами был не менее 30º и не более 150º.

После обвода берут соответственно отсчеты n2, и n¹2. Вычисляют обведенную площадь в делениях планиметра дважды:

N1 = n2- n1, и N2=n¹2 - n¹1.

Если эти значения отличаются в пределах не более 4 единиц отсчета, то вычисляют среднее значение N_ср

N _ср. = N₁ + N₁/2

и определяют относительную цену деления μ по формуле

Вычисленное значение μ соответствует определенной длине рычага R, которую запоминают. При этих двух параметрах на данном листе карты можно измерить площадь любого контура. Порядок действий по измерению площади такой же, как при определении цены деления. Величину площади вычисляют по формуле:

S = μ Nср

Основной задачей изучения вопросов по проектированию сельскохозяйственных угодий является ознакомление с принципами и этапами проектирования, а также практическое применение графического, аналитического и механического способов построения фигур заданной площади.

Тема 7 Геометрическое нивелирование См. Метод.Указание геометрическое нивелирование по летней практике

Тема 8 Тахеометрическая съемка

46