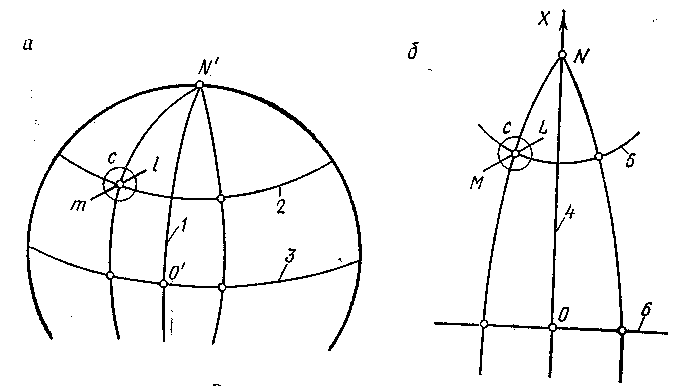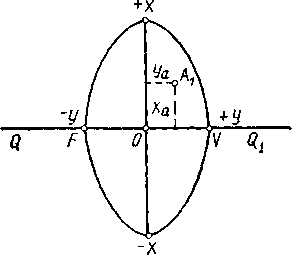Плоские прямоугольные координаты Гаусса

Применение координат Гаусса в геодезии обусловлено необходимостью проектировать поверхность сфероида (эллипсоида вращения) на плоскость.

Существует много способов проектирования поверхности сфероида на плоскость.

Для топографо-геодезических целей предпочитают проекцию, сохраняющую углы, но искажающую длины отрезков линий и площади. Такая проекция называется конформной. Она обладает свойством сохранять подобие бесконечно малых фигур.

Рис. 2.7 К проекции Гаусса

Применяя конформную проекцию Гаусса, поверхность земного сфероида разделяют на зоны меридианами. Средний меридиан каждой зоны изображается на плоскости прямой линией и без искажений. Такой меридиан называется осевым (меридиан N/O/), а его изображение на плоскости

принимают за ось абсцисс (прямая ON).Началом координат и каждой зоне считают точку О - пересечение изображений осевого меридиана и экватора (прямой, принимаемой за ось ординат) (см рис. 7а)

В проекции Гаусса все меридианы, кроме осевого, и все па­раллели сфероида на плоскости изобразятся кривыми линиями. В конформной проекции искажение изображения линий малой длины и пределах небольшого участка будет одинаковым во всех направлениях, т.е. сохраняется постоянство масштаба. Если ml=s - отрезок малой длины на сфероиде, a ML=S - его изображение на плоскости в проекции Гаусса, то масштаб изо­бражения можно определить по приближенной формуле: = 1+, где y – ордината средней точки C линии ML, а R – средний радиус кривизны земного эллипсоида в этой же точке.

Изменение ΔS=S-s длины линии s при изображении ее на плоскости вычисляется по формуле: ΔS= s, откуда следует, что чем дальше в этой проекции точка с (см. рис. 2. 7б) находится от среднего меридиана, тем она с большим смещением будет нанесена на плоскость. Чтобы возникающие при этом искажения расстояний не выходили за установленные пре­делы, поверхность земного эллипсоида делят на шестиградусные зоны. Счет зон ведут от начального (Гринвичского) меридиана к востоку.

Рис. 8 Проекция 6-градусной зоны на плоскости

Расстояние от точки О до крайних точек F и V для шестиградусных зон равно 3°, а у≈330 км. В зональной системе прямоугольных координат положение на плоскости, например, точки А1, являющейся изображением точки А земного эллипсоида, определяется координатами ха и уа в проекции Гаусса. В каждой зоне координаты х и у могут иметь положительные и отрицательные значения. Абсциссы считаются положительны­ми, если их отсчитывают от экватора к северу, и отрицатель-

ными, если к югу. Ординаты, отсчитываемые от осевого меридиана к востоку, - положительные, а к западу – отрицательные.

В этой системе координат для всех точек на территории России абсциссы имеют положительные значения. Во избежание отри­цательных ординат (для удобства при вычислениях) в нашей стране для шестиградусных зон принято условно считать ординату точки О, равной не нулю, а 500 км. В таком случае ординаты (так же, как и абсциссы) всех точек каждой зоны в России будут иметь поло­жительные значения (наибольшая ширина шестиградусной зоны не превышает 385 км). Чтобы знать, в какой зоне лежит данная точка, впереди ее ординаты пишут номер зоны, т.е. пользуются условными значениями ординат.