2.1.Интегральная и дифференциальная функции распределения. Вероятность попадания в заданный интервал.

Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях.

Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой зависимости). При соблюдении некоторых не очень жестких условий указанная сумма случайных величин подчиняется приближенно нормальному закону распределения и тем точнее, чем большее количество величин суммируется.

Ни одна из суммируемых случайных величин не должна резко отличаться от других, т. е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию.

Для примера рассмотрим изготовление некоторой детали на станке-автомате. Размеры изготовленных деталей несколько отличаются от требуемых. Это отклонение размеров от стандарта вызывается различными причинами, которые более или менее независимы друг от друга. К ним могут относиться:неравномерный режим обработки детали; неоднородность обрабатываемого материала; неточность установки заготовки в станке; износ режущего инструмента и деталей станков; упругие деформаций узлов станка; состояние микроклимата в цехе; колебание напряжения в электросети и т. д. Каждая из перечисленных и подобных им причин влияет на отклонение размера изготовляемой детали от стандарта. Таким образом, общее отклонение размера, фиксируемое измерительным прибором, является суммой большего числа отклонений, обусловленных различными причинами. Если ни одна из этих причин не является доминирующей, то суммарное отклонение является случайной величиной, имеющей нормальный закон распределения.

Так как нормальному закону подчиняются только непрерывные случайные величины, то это распределение можно задать в виде плотности распределения вероятности.

 Определение: Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

8.Вероятность попадания в заданный интервал нормальной случайной величины.

Нормально распределенные непрерывные случайные величины встречаются в практических задачах чаще всего. Это связано, в частности, с Центральной предельной теоремой Ляпунова, которая утверждает, что если случайная величина порождена несколькими примерно равными по силе причинами, то она становится нормально (или почти нормально) распределенной.  Плотность (дифференциальная функция) нормального распределения равна

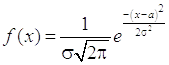,  т.е. зависит от двух параметров: математического ожидания a и среднего квадратического отклонения . Интегральная функция нормального распределения связана с функцией Лапласа 

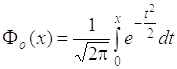, значения которой берутся из таблиц (см.ниже). Для вычисления вероятности того, что нормально распределенная случайная величина X будет принимать значения в промежутке используется формула 

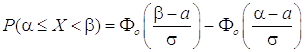
9. Каждая случайная величина полностью определяется своей функцией распределения.

В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.

 

Математическое ожидание случайной величины

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Математическое ожидание дискретной случайной величины x , имеющей распределение

x1	x2	...	xn
p1	p2	...	pn

Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_x(x) вычисляется по формуле . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x , h = f(x), то

Основные свойства математического ожидания:

• математическое ожидание константы равно этой константе, Mc=c ;

• математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и bсправедливо: M(ax + bh ) = a M(x )+ b M(h );

• математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).

 

Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )².

Легко показать, что Dx = M(x - Mx )²= Mx ² - M(x )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

10.Схема повторных испытаний. Формула Бернулли. Предельные теоремы в схеме Бернулли (Пуассона, Муавра-Лапласа).

Формула Бернулли

Если при одних и тех же условиях определенный опыт повторяется n раз и если вероятность появления некоторого события А в каждом опыте равна р, то вероятность того, что событие А в серии из n опытов произойдет ровно к раз, находится по формуле Бернулли:

Сочетания из n по к находят по формуле

Число к появлений события А в серии из n опытов, вероятность которого наибольшая, называется наивероятнейшим числом наступления события А в n опытах. Это число находят по формуле

к = [np + р]. (2)

Символ [...] означает здесь целую часть числа.

Если число np + р - целое, то наивероятнейшим будет также и число к0 - 1 с той же вероятностью Pn (к0).

Пример 6.15. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две детали будут нестандартными. Каково наивероятнейшее число нестандартных деталей в рассматриваемой выборке из 30 деталей и какова его вероятность?

Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - появление нестандартной детали; его вероятность Р = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли находим:

P30 (2) = C0 (0,04)2 (0,96)28 » 0,202.

Наивероятнейшее число нестандартных деталей в данной выборке вычисляется по формуле (2):

к0 = [30 ¦ 0,04 + 0,04] = [1,24] = 1, а его вероятность равна

P30(1) = C1c • 0,041 • (0,96)29 » 0,305.

Пример 6.16. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность того, что в серии из четырех выстрелов будет: а) хотя бы одно попадание; б) не менее трех попаданий; в) не более одного попадания.

Решение. Здесь n = 4, p = 0,8, q = 0,2. а) Найдем вероятность противоположного события - в серии из четырех выстрелов нет ни одного попадания в цель:

Отсюда находим вероятность хотя бы одного попадания в цель:

б) Событие В, заключающееся в том, что в серии из четырех выстрелов произошло не менее трех попаданий в цель, означает, что было либо три попадания (событие С), либо четыре (событие D), т. е. В = С + D. Отсюда P (B) = P (C) + P (D); следовательно,

в) Аналогично вычисляется вероятность попадания в цель не более одного раза: 

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

1. Предмет и основные задачи математической статистики

Матем статистика- раздел математики, изучаю-щий математические методы сбора, системати-зации, обработки и интерпретации результатов наблюдений с целью выявления статистических закономерностей. Матеем статистика опирается на теорию вероятностей. Если теория вероятно-стей изучает закономерности случайных явлений на основе абстрактного описания действительно-сти (теоретической вероятностной модели), то матем статистика оперирует непосредственно результатами наблюдений над случайным явле-нием, представляющими выборку из некоторой конечной или гипотетической бесконечной гене-ральной совокупности. Используя результаты, полученные теорией вероятностей, матем стати-стика позволяет не только оценить значения искомых характеристик, но и выявить степень точности получаемых при обработке данных выводов.  Математическая статистика по наблюденным значениям оценивает вероятности этих событий либо осуществляет проверку предположений относительно этих вероятностей. В матем стати-стике, наоборот, исследование связано с кон-кретными данными и идет от практики к гипоте-зе и ее проверке.

2. Классификация статистической информации.

Статистическая информация - это разновидность экономической информации, содержащей различные сведения социально-экономического характера, которые можно фиксировать, передавать, преобразовывать, хранить и использовать для решения социальных и экономических задач.

Классификация статистической информации предусматривает ее деление по ряду общих признаков, а также характерных признаков, имеющих принципиальное значение для непосредственной машинной обработки.

Сначала рассмотрим классификацию информации по ряду общих признаков.

Четко определенный круг источников информации для каждого уровня системы Госкомстата РФ позволяет классифицировать статистическую информацию по месту ее возникновения. Ее источниками являются: на районном и областном уровне - предприятия и организации; на федеральном - министерства и ведомства, отчетность которых не централизована в органах государственной статистики.

По принадлежности к отрасли экономики можно выделить статистическую информацию по промышленности, окружающей среде и сельскому хозяйству, основным фондам и строительству, услугам, транспорту и связи и т.д.

По способу представления статистическая информация подразделяется на почтовую, которая по периодичности поступлениябывает ежедневной, декадной, месячной, квартальной, полугодовой, годовой и единовременной, и срочную, которая передается по телеграфным и телефонным каналам связи и обычно бывает ежедневной, декадной, месячной периодичности.

На основании рассмотренной общей классификации статистической информации выделим ряд признаков, имеющих принципиальное значение при машинной обработке.

Прежде всего, на каждом уровне обработки статистическую информацию по назначению подразделяют на входную и выходную. При этом

22

входная и выходная информация бывает внутренней и внешней по отношению к органам государственной статистики. Внутренняя - информация, циркулирующая в самой системе Госкомстата РФ, а внешняя - информация, получаемая от различных отчитывающихся организаций и органов управления.

Классификация информации по указанным признакам необходима для того, чтобы знать общие объемы входной и выходной информации для определения пропускной способности информационно-вычислительной сети Госкомстата РФ и организации дальнейшего информационного взаимодействия с другими ЭИС.

Внутреннюю входную (выходную) информацию, передаваемую с одного уровня на другой, можно представлять в различной форме (на бланках отчетов, в телетайпограммах и на магнитных носителях в виде электронных таблиц).

В зависимости от способа обработки на каждом из уровней статистическую информацию подразделяют на первичную, внутримашинную (промежуточную) и сводную.

Первичная (входная) информация возникает непосредственно в местах источников информации и является основой получениясводной (выходной) информации после ее соответствующей машинной обработки с помощью заданного алгоритма.

Внутримашинная информация возникает в процессе преобразования первичной информации в сводную. Она содержит накапливаемые и перерабатываемые данные и может храниться в памяти ПЭВМ или чаще на различных машинных носителях для последующего использования.

Классификация статистической информации по способу обработки позволяет учесть особенности решения статистических задач, что в значительной степени определяется структурой внутримашинной информационной базы.

По степени стабильности статистическая информация бывает условно-постоянной и переменной. К условно-постоянной относится информация, которая остается неизменной длительное время и многократно используется в процессе машинной обработки (справочная информация, данные прошлых периодов и плановые данные и др.).

Переменная информация содержит фактические данные за соответствующий период, содержащиеся в первичных статистических отчетах, которые меняются в зависимости от периодичности поступления.

Классификация статистической информации по степени стабильности необходима для более точного определения и последующей организации массивов постоянной информации, которые можно будет эффективно

23

использовать при машинной обработке, значительно сокращая объемы работ по вводу данных в ПЭВМ.

При проектировании ИТ важно определить потоки информации, т.е. организованное в пределах информационной системы движение данных от источников информации к потребителю.

В результате анализа информационных потоков выявляются оптимальные уровни обработки и передачи информации, динамика генерирования потока данных источниками и потребителями.

В органах государственной статистики можно выделить несколько стандартных схем потоков информации (рис. 2.2). Источником статистической информации, представляемой в органы государственной статистики, являются предприятия и организации различных отраслей экономики. Каждая отрасль экономики имеет определенный круг утвержденных статистических отчетов, которые в соответствии с табелем отчетности должны быть представлены органам статистики.

Статистическая отчетность, как правило, проходит последовательную (децентрализованную) обработку на всех уровнях системы Госкомстата РФ, где на каждом уровне осуществляется сводно-группировочная обработка данных по различным признакам (территориям, ведомствам и т.д.).

Обычно первичные отчеты поступают от предприятий и организаций на районные и региональные уровни по министерствам, отчетность которых не централизована в органах государственной статистики, на федеральный уровень, где производится автоматизированное получение различных сводных отчетов в соответствующем территориальном разрезе.

Сводная отчетность районного уровня представляется потребителям (территориальным органам управления и вышестоящим уровням системы Госкомстата РФ). При этом используется как почтовый способ представления информации (отчеты, магнитные носители), так и по каналам связи (электронная почта). Запись информации на магнитные носители осуществляется как правило в месте поступления первичных отчетов.

3. Понятия “генеральная совокупность”, “выборочная совокупность” и “репрезентативная совокупность ”. Способы выбора из генеральной совокупности.

Генеральная совокупность – все множество имеющихся объектов.

Понятия генеральной совокупности и выборки из нее являются основополагающими в статистике.

Строгие определения заимствованы из теории вероятностей, хотя терминология этих двух наук различается. Вместо случайной величины  в теории вероятностей, в математической статистике вводится понятие о генеральной совокупности. Под генеральной совокупностью понимают множество всех возможных значений случайной величины

Выборочной совокупностью (или выборкой) называют совокупность случайно отобранных объектов.

Выборка из генеральной совокупности— ограниченный набор реально наблюдаемых выборочных из генеральной совокупности значений, описывающих исследуемый объект или явление. Количество этих значений называется объемом выборки.

Существуют пять основных способов организации выборочного наблюдения:

1. простой случайный отбор, при котором  объектов случайно извлекаются из генеральной совокупности объектов (например с помощью таблицы или датчика случайных чисел), причем каждая из возможных выборок имеют равную вероятность. Такие выборки называются собственно-случайными;

2. простой отбор с помощью регулярной процедуры осуществляется с помощью механической составляющей (например, даты, дня недели, номера квартиры, буквы алфавита и др.) и полученные таким способом выборки называются механическими;

3. стратифицированный отбор заключается в том, что генеральная совокупность объема  подразделяется на подсовокупности или слои (страты) объема  так что . Страты представляют собой однородные объекты с точки зрения статистических характеристик (например, население делится на страты по возрастным группам или социальной принадлежности; предприятия — по отраслям). В этом случае выборки называютсястратифицированными (иначе, расслоенными, типическими, районированными);

4. методы серийного отбора используются для формирования серийных или гнездовых выборок. Они удобны в том случае, если необходимо обследовать сразу "блок" или серию объектов (например, партию товара, продукцию определенной серии или население при территориально-административном делении страны). Отбор серий можно осуществить собственно-случайным или механическим способом. При этом проводится сплошное обследование определенной партии товара, или целой территориальной единицы (жилого дома или квартала);

5. комбинированный (ступенчатый ) отбор может сочетать в себе сразу несколько способов отбора (например, стратифицированный и случайный или случайный и механический); такая выборка называется комбинированной.

1. 4. Статистическое распределение выборки. Эмпирическая функция распределения. Графическое изображение статистического распределения.

Пусть из генеральной совокупности извлечена выборка, причем наблюдалось n_t раз, х₂ - п₂ раз,  раз и  - объем выборки. Наблюдаемые значения  - называют вариантами, а последовательность вариант, записанных в возрастающем порядке,— вариа­ционным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки  — относи­тельными частотами.

Статистическим распределением выборки называют пе­речень вариант и соответствующих им частот или относи­тельных частот. Статистическое распределение можно за­дать также в виде последовательности интервалов и соответ­ствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математи­ческой статистике — соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.

Пример. Задано распределение частот выборки объема я = 20:

     2     6     12

     3      10      7

    Написать распределение относительных частот.

Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки:

=3/20 = 0,15,  W₂= 10/20 = 0,50, W₃ = 7/20 = 0,35.

Напишем распределение относительных частот:

  x_i     2         6           12

W_i     0,15     0,50     0,35

Контроль: 0,15+0,50+ 0,35= 1.

Эмпирической функцией выборки (функцией распределения выборки) называется функция

Fn(x)=	nx
	n

 

, которую можно записать в следующем виде:

 

  Данная функция непрерывная, кусочно-постоянна и изменяется в каждой точке х_i, гдех_i — варианта рассматриваемого статистического распределения. 

  Пример

  По заданной выборке построить эмпирическую функцию выборки. 

хi	2	4	5	6	7
ni	5	3	4	5	3

F20(X≤2)=	0	=0
	20

F20(4)=	5	=0.25
	20

F20(5)=	5+3	=0.4
	20

F20(6)=	5+3+4	=0.6
	20

F20(7)=	5+3+4 +5	=0.85
	20

F20(X>7)=	5+3+4 +5 +3	=1
	20

 

5.Числовые характеристики распределений: мода, медиана, среднее

Числовые характеристики статистического распределения: выборочное среднее, оценки дисперсии, оценки моды и медианы, оценки начальных и центральных моментов. Статистическое описание и вычисление оценок параметров двумерного случайного вектора.

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины.

К   характеристикам   распределения,   описывающим   количественно   его   структуру   и строение, относятся:

•    характеристики положения;

•     рассеивания;

•    асимметрии и эксцесса.

Оценка  центральной тенденции

К характеристикам положения относятся следующие оценки центральной тенденции: мода

(Мо), медиана (Ме), квантили и среднее арифметическое ( M ).

Важное  значение  имеет  такая  величина  признака,  которая  встречается  чаще  всего  в

изучаемом ряду, в совокупности. Такая величина называется модой (Мо). В дискретном ряду Мо определяется  без  вычисления,  как  значение  признака  с  наибольшей  частотой  (например,  по данным таблицы 2.1. Мо= 13).

При расчете моды может возникнуть несколько ситуаций:

1. Два значения признака, стоящие рядом, встречаются одинаково часто. В этом случае мода равна среднему арифметическому этих двух значений. Например, в следующем ряду данных:

12, 13, 14, 14, 14, 16, 16, 16, 18, 19

Мо= (14+16)/2= 15.

2. Два значения, встречаются также одинаково часто, но не стоят рядом. В этом случае говорят, что ряд данных имеет две моды, т.е. он бимодальный.

3. Если все значения данных встречаются одинаково часто, то говорят, что ряд не имеет

 

моды.

 

Чаще всего встречаются ряды данных с одним модальным значением признака. Если в

 

ряду данных встречается два или более равных значений признака, то говорят о неоднородности совокупности.

Вторая числовая характеристика ряда данных называется медианой (Ме) – это такое значение признака, которое делит ряд пополам. Иначе, медиана обладает тем свойством, что половина всех выборочных значений признака меньше её, половина больше. При нечетном числе элементов в ряду данных, медиана равна центральному члену ряда, а при четном среднему арифметическому двух центральных значений ряда. В нашем примере (таблица 2.1.) Ме=(13+13)/2=13. Вычисление медианы имеет смысл только для порядкового признака.

Среднее арифметическое значение признака:

где xi – значения признака, n – количество данных в рассматриваемом ряду.

Среднее   арифметическое  значение  признака,  вычисленное  для   какой-либо  группы,

интерпретируется как значение наиболее типичного для этой группы человека. Однако бывают случаи,  когда  подобная  интерпретация  несостоятельна  (в  случае,  если  существует  большая разница между минимальным и максимальным значениями признака).

Квантиль   –  это  такое  значение  признака,  которое  делит  распределение  в  заданной пропорции:  слева  0,5%,  справа  99,5%;  слева  2,5%,  справа  97,5%  и  т.п.  Обычно  выделяют

следующие разновидности квантилей:

1)   Квартили Q1, Q 2, Q3 – они делят распределение на четыре части по 25% в каждой;

2)   Квинтили К1, К2, К3, К4 – они делят распределение на пять частей по 20% в каждой;

3)   Децили D1, ...,D9, их девять, и они делят распределение на десять частей по 10% в каждой;

каждой части.

Поскольку процентиль – наиболее мелкое деление, то все другие квантили могут быть представлены через процентили. Так, первый квартиль – это двадцать пятый процентиль, первый квинтиль – второй дециль или двадцатый процентиль, и т.п

Для характеристики рядов распределения (структуры вариационных рядов), наряду со средней, используются т. н. структурные средние: мода и медиана. Мода и медиана наиболее часто используются в экономической практике.

Мода- варианта, которая наиболее часто встречается  в ряду распределения (в данной совокупности).

В дискретных вариационных рядах мода определяется по наибольшей частоте. Предположим товар А реализуют в городе 9 фирм по следующим ценам в рублях:

44; 43; 44; 45; 43; 46; 42; 46;43. Так как чаще всего встречается цена 43 рубля, то она и будет модальной.

При характеристике социальных групп населения по уровню дохода следует использовать модальное значение, нежели среднее. Средняя будет занижать одни показатели и завышать другие — тем самым осредняя (уравнивания) доходы всех слоев населения.

Мода применяется для решения некоторых практических задач. Так, например, при изучении товарооборота рынка берется модальная цена, для изучения спроса на обувь, одежду используют модальные размеры обуви и одежды.

Медиана- это численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда (построенного в порядке возрастания, либо убывания значений изучаемого признака). Медиану иногда называют серединной вариантой, т.к. она делит совокупность на две равные части таким образом, чтобы по обе ее стороны находилось одинаковое число единиц совокупности. Если всем единицам ряда присвоить порядковые номера, то порядковый  номер медианы будет определяться по формуле (n+1):2 для рядов, где n — нечетное. Если же ряд с четным числом единиц, то медианойбудет являться среднее значение между двумя соседними вариантами, определенными по формуле: n:2, (n+1):2, (n:2)+1.

В дискретных вариационных рядах с нечетным числом единиц совокупности — это конкретное численное значение в середине ряда.

6. Генеральная средняя.

Пусть изучается генеральная совокупность относительно количественного признака Х.

  Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Если все значения признака различны, то

Если значения признака имеют частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то