24. Изображение синусоидальных величин с помощью векторов. Сложение и вычитание синусоидальных величин

При расчете цепей переменного тока часто прихо­дится производить операции сложения и вычитания токов и напряжений. Когда токи и напряжения заданы аналитически или временными диаграммами, эти опе­рации оказываются весьма громоздкими. Существует метод построения векторных диаграмм, который позво­ляет значительно упростить действия над синусоидаль­ными величинами. Покажем, что синусоидальная вели­чина может Сыть изображена вращающимся вектором.

Изображение синусоидальных величин с помощью векторов дает возможность наглядно показать началь­ные фазы этих величин и сдвиг фаз между ними.

На векторных диаграммах длины векторов соответ­ствуют действующим значениям тока, напряжения и ЭДС так как они пропорциональны амплитудам этих величин.

Совокупность нескольких векторов, соответствую­щих нулевому моменту времени, называют вектор­ной диаграммой. Необходимо иметь в виду, что на векторной диаграмме векторы изображают токи (напряжения) одинаковой частоты.

Синусоидальные величины можно складывать 3 способами: 1) Аналитическим 2) Графическим 3)Синусоид величина представлена в виде вектора. 2 вектора склад по методу паролеллограмма.

Вектор отражает синусоид напряжение, где модуль равен действующему напряжению. Это нач фаза. Углы от 0 против часовой стрелки берутся с +, по с -.

Чтобы вычесть вектор, надо изм его направление противоположное и сложить с первым.

225. Характеристика цепи с активным сопротивлением, с индуктивностью. Цепь с активным сопротивлением и индуктивностью

Цепь с R: На зажимах цепи переменного тока действует на­пряжение Так как цепь обладает только активным сопротивлением, то, согласно закону Ома для участка цепи, , где представляет собой выражение закона Ома для амплитудных значений. Разделив левую и правую части этого выражения на получим за­кон Ома для действующих значений: I=U/R.

Сопоставляя выражения для мгновенных значений тока и напряжения, приходим к выводу, что токи и напряжения в цепи с активным сопротивлением совпа­дают по фазе.

Цепь в L: Под действием синусоидального напряжения в цепи с индуктивной катушкой без ферромагнитного сердечника проходит синусоидальный ток . В результате этого вокруг катушки воз­никает переменное магнитное поле и в катушке и на­водится ЭДС самоиндукции. При R=0 напряжение источника целиком идет на уравновешивание этой ЭДС; следовательно .

Сопоставляя выражения для мгновенных значения тока и напряжения, приходим к выводу, что ток в цепи с индуктивностью отстает по фазе от напряже­ния на угол п/2.

Цепь с RL: состоит из участков, свойства которых известны. Проанализируем работу данной цепи. Пусть ток е цепи изменяется по закону . Тогда напряжение на активном сопротивлении так как на этом участке напря­жение и ток совпадают по фазе. Напряжение на ка­тушке , поскольку на индуктивности напряжение опережает по фазе ток на угол п/2. Построим векторную диаграмму для рассматриваемой цепи. Сначала откладываем вектор тока I.

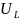затем вектор напряжения совпадающий по фазе с вектором тока. Начало вектора опережающего вектор тока на угол п/2, соединим с концом век­тора для удобства их сложения. Суммарное на­пряжение изображается векто­ром U, сдвинутым по фазе относительно вектора тока на угол . Векторы U образуют треуголь­ник напряжений. Выведем закон Ома для этой цепи. На основании теоремы Пифагора для треуголь­ника напряжений имеем 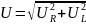. Введем обозначение , где Z — полное сопротивление цепи. Тогда выражение закона Ома примет вид I=U/Z. Так как полное сопротивление цепи Z определя­ется по теореме Пифагора, ему соответствует треуголь­ник сопротивлений. Поскольку при последовательном соединении напряжения на участках прямо пропорциональны сопротивлениям, треуголь­ник сопротивлений подобен треугольнику напряжений. Сдвиг фаз между током и напряжением определя­ется из треугольника сопротивлений:

, .