11) Метод наложения. Применение 2-х законов Кирхгофа для расчёта

цепей.

Метод наложения основан на принципе независимой работы каждой ЭДС. Каждая ЭДС дает частичные токи истинного направления. Алгебраическая сумма этих частичных токов дает истинные токи. Если при расчете ток получается отрицательный -значит истинное направление противоположно заданному. Для проверки правильности расчетов можно использовать первый закон Кирхгофа (сумма токов ,подходящих к узлу, равна сумме токов, отходящих от узла). 2 закон Кирхгофа может использоваться для расчетов замкнутых контуров. В контуре алгебраическая сумма электродвижущих сил будет равна алгебраической сумме падений напряжений на элементах.

12) Метод узловых потенциалов, особенности расчёта цепей

Метод узловых потенциалов основан на том, что определяются потенциалы узлов и далее по правилу «ток течет от большего потенциала к меньшему». Определяем токи. Если при расчетах значение тока отрицательное, то его направление противоположно заданному. Порядок расчета: задаемся произвольным направлением токов. Сначала 1 из узлов принимаем за нулевой потенциал. Определяем проводимости резисторов g=1/R, ветвей и узлов. Составляется система уравнений. Решение системы позволяет найти потенциалы всех узлов. Далее определяем ток по известным потенциалам. Правильность расчетов можно проверить 1 законом Кирхгофа, или балансом мощностей.

13) Метод контурных токов, особенности расчёта цепей.

Метод контурных токов используется для расчета сложных цепей независимо от количества источников питания (ЭДС). Метод контурных токов позволяет уменьшить количество уравнений до минимума. За основу расчета берется выбор независимых контуров (Например трёх) с условием прохождения по каждому замкнутому контуру 1 контурного тока. Порядок расчета: задаемся произвольным направлением токов. Если при расчетах ток получится отрицательным -значит он направлен в противоположную сторону. В каждом из выбранных контуров выбираем произвольное направление обхода контура (контурный ток). Следую по направлению заданного контурного тока составляем уравнение по 2 закону Кирхгофа. Если направление ЭДС совпадает с направлением обхода -берется со знаком +. В полученной системе уравнений подставляем значения и упрощаем ее. Далее находим определитель для каждого уравнения методом матрицы. Определив все , определяем контурные токи по формуле I= / . Потом

определяем истинные токи, учитывая взаимные направления контурных токов. Найденные истинные токи можно проверить по 1 закону Кирхгофа, или балансом мощностей.

14) Метод эквивалентного генератора, особенности расчёта тока в ветви.

Метод эквивалентного генератора (МЭГ) используется тогда, когда надо определить ток в какой-нибудь ветви. Принцип расчета: Разрываем ветвь, в которой хотим определить ток, в ветви убираются сопротивления. Нам надо найти на разрыве. Далее надо найти R по отношению к точкам разрыва ( . Далее определяем ток по формуле (в данном случае -это сопротивление, которое находилось на разрыве). Для нахождения напряжения холостого хода надо определить потенциалы прилегающих узлов, для этого можно применять любой метод расчета. 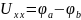. Для определения надо закоротить все ЭДС (то есть убрать со схемы) и оставить одни сопротивления. = где и это общие сопротивления оставшихся резисторов, то есть равен общему сопротивлению оставшихся на схеме резисторов. Если при расчете не явно выражена параллельность соединенных ветвей, то используют преобразование из треугольника в звезду и наоборот