7) Схема замещения электрической цепи. Работа, мощность, баланс мощностей.

Схема замещения -это схема, подготовленная для расчетов. На ней расставляются токи, напряжения и осуществляется расчет. Источник тока совершает работу по перемещению заряда в замкнутой цепи. A=EQ. Также работу можно выразить: т.к I=Q/t, то работа равна A=EIt. Согласно закону сохранения энергии, мощность, отдаваемая источником, всегда будет равна сумме мощностей всех потребителей. Равенство мощности, отдаваемой источником, и суммы всех мощностей потребителей называется баланс мощностей. P=IU= = /R.

8) Простейшая электрическая цепь с одним источником. Режим холостого хода и короткого замыкания.

Источник энергии может работать в режиме холостого хода и короткого замыкания. 1) Режим ХХ. В данном режиме ключ разомкнут. Ток отсутствует, падение напряжения внутри источника отсутствует. Напряжение источника равно . (точка a расположена перед ключом, точка b-после сопротивления).2) Режим КЗ: режим КЗ наступает, когда в цепи отсутствует сопротивление (нагрузка). При КЗ в источнике выделяется мощность, равная мощности источника, это приводит к большому выделению тепла и выходу источника из строя. Режим КЗ опасен для цепей.

9) Электрическая цепь с двумя источниками. Противо эдс. Потенциальная диаграмма и её построение.

При наличии 2 ЭДС каждая ЭДС создает свой ток, независимо от другой. Общий ток равен алгебраической сумме этих токов. ЭДС, через которую протекает ток противоположного направления, называется противоЭДС и является приемником эл. энергии. То есть напряжение на ЭДС-приемнике равно E+ , а на ЭДС-генераторе E- . Потенциальная диаграмма-это определение потенциалов в любой точке замкнутого контура. Она дает возможность без расчетов определить напряжение между любыми точками схемы. Для построения потенциальной диаграммы 1 точку принимаем за нулевой потенциал, выбираем направление обхода контура. Расставляем точки после каждого элемента и определяем их потенциал. Потенциал каждой последующей точки равен разности потенциала предыдущей точки и падения напряжения на сопротивлении (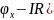 . Если между потенциалами не сопротивление, а ЭДС, то потенциал определяется по формуле: сумма потенциала предыдущей точки и ЭДС ( (если ЭДС направлена в определяемую точку, то берется со знаком +, если в противоположную сторону, то со знаком -). При построении диаграммы по горизонтальной оси откладывается сопротивление, по вертикальной-потенциал.

10) Законы Кирхгофа. Метод свёртывания схемы.

В любой схеме, как простой, так и сложной присутствует 3 закона: закон Ома и 2 закона Кирхгофа. 1 закон Кирхгофа: алгебраическая сумма токов, подходящих к узлу равна сумме токов, отходящих от узла. А алгебраическая сумма всех токов, подходящих со знаком +, отходящих со знаком -, равна нулю. 2 закон Кирхгофа: алгебраическая сумма ЭДС равна сумме падений напряжения на всех элементах. Сложные цепи можно рассчитывать методом свертывания. Этот метод заключается в том, чтобы, определяя общие сопротивления, свернуть схему в простую. Затем можно определять токи. Если ток со знаком -, значит он направлен противоположно указанному направлению.