41) Соединение приемников энергии «треугольником» при 2-х системах нагрузки.

Симметричная нагрузка

При симметричной нагрузке Zab = Zbc = Zca = Zej , т.е. Zab = Zbc = Zca = Z, ab = bc = ca = .

Так как линейные (они же фазные) напряжения UAB, UBC, UCA симметричны, то и фазные токи образуют симметричную систему İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca.

Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°.

Линейные токи

İA = İab - İca; İB = İbc - İab; İC = İca - İbc;

образуют также симметричную систему токов

На векторной диаграмме фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т.е. φ > 0°). Здесь принято, что напряжение UAB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в раз. Линейный ток İA отстает по фазе от фазного тока İab на угол 30°, на этот же угол отстает İB от İbc, İC от İca.

Таким образом, при соединении треугольником действующее значение линейного тока при симметричной нагрузке в раз больше действующего значения фазного тока и UЛ = UФ; IЛ =IФ.

При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы.

Фазное напряжение UФ = UЛ. Фазный ток IФ = UФ / ZФ, линейный ток IЛ =IФ, угол сдвига по фазе φ = arctg (XФ / RФ).

Несимметричная нагрузка приемника

В общем случае при несимметричной нагрузке Zab ≠ Zbc ≠ Zca. Обычно она возникает при питании от трехфазной сети однофазных приемников. При расчете для несимметричной нагрузки сначала определяют значения фазных токов İab, İbc, İca и соответствующие им сдвиги фаз φab, φbc, φca. Затем определяют линейные токи с помощью уравнений в комплексной форме или с помощью векторных диаграмм.

42) Мощности 3-х фазной цепи.

Активная мощность трёхфазной цепи равна сумме активных мощностей её фаз: P=Pл+Рв+Рс

Реактивная мощность трёхфазной цепи равна сумме реактивных мощностей её фаз: Q=Qа+Qв+Qс

Очевидно, что в симметричной трехфазной цепи

Ра=Рв=Рс=Рф, Qа=Qв=Qс=Qф , тогда Р=3Рф, Q=3Qф

Мощность одной фазы определяется по формулам для однофазной цепи:

,

Эти формулы можно использовать для расчёта мощности симметричной трёхфазной цепи, однако измерения фазных напряжений и токов связано с тем, что не всегда есть доступ к нулевой точке, которая не всегда имеет специальный вывод и находиться внутри машины, поэтому формулы мощности записываются через линейные токи и напряжения.

При соед «звездой»:

При соед «треугольником»:

Таким образом, в обоих случаях активная мощность сим цепи:

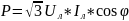
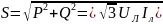Реактивная: , полная мощность: , коэф мощности:

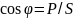
43) Причины возникновения несинусоидальных напряжений и токов. Виды несинусоидальных кривых.

Нелинейность элементов является главной причиной возникновения несинусоидального токов и напряжения (конденсатор, сегмето-электрик и др.), а также несинусоидальностью источника питания. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами, катушка с железным сердечником. Выпрямитель на диоде (диод не линейный элемент, после выпрямления мы получаем постоянные импульсы в отношении направления тока и напряжения, полученные импульсы явл несинусоидальными величинами.

Несинусоидальные величины разделяются на 3 вида:

- кривые, относительно абсцисс Если 2м её обциссам различающимся на половину периоду, соответствует равные по величине, но противоположные по знаку координаты.

-кривые, относительно ординат Если 2м её равным по величине, но противоположным по знакам обциссам соответствует один по величине и знаку ординаты.

-кривые, относительно начала координат 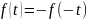Если любым двум абциссам, имеющим одинаковые значения, но разные знаки соответствует ординаты равные по величине, но разные по знаку.