30. Резонанс напряжений

Резонансом напряжений называют явление в цепи с последовательным контуром, когда ток в цени совпадает по фазе с напряжением источника.

Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление должно быть равно нулю, так как Таким образом, условием резонанса напряжений является Х=0 или X_L = X_C .Но X_L=2пfL, а Х_с = 1/(2п/С). В ре­зультате можно записать 2пfL=1/(2пfС).

При резонансе напряжений частота источника равна собственной частоте колебаний контура.

Признаки резонанса напряжений:

а) сопротивление цепи Z = R минимальное и чисто активное;

б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;

в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажи­мах цепи.

Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие по­терь в контуре. Напряжение на катушке и конденса­торе обусловлено накопленной в них энергией, значение которой тем больше, чем меньше потерн с цепи. Количественно указанное явление характеризуется добротностью контура Q, которая представ­ляет собой отношение напряжения на катушке или конденсаторе к напряжению на зажимах цепи при резонансе.

Способность колебательного контура выделять токи резонансных частот и ослаблять токи других час­тот характеризуется резонансной кривой. Резонансная кривая показывает зависимость дей­ствующего значения тока в контуре от частоты источ­ника при неизменной собственной частоте контура.

Резонанс напряжений широко используется в ра­диотехнике и электронике для выделения сигналов за­данной частоты.

31. Формы записи комплекных чисел. Арифметические действия над комплексными числами

Комплексный метод расчета цепей переменного тока применяется для облегчения решения задач, по расчету сложных цепей переменного тока. Особенно это проявляется в расчетах разветвленных цепей (параллельное соединение элементов) т.к. обычный метод очень сложен. Основное преимущество этого метода заключается в том, что выразив эл величины в комплексной форме, мы дальше производим расчет представляя цепь, цепью постоянного ток и забываем о треугольниках. 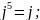Основной величиной в комплексной форме явл мнимая единица: Существуют 3 формы записи комплексных чисел: 1) Алгебраическая: ; ОА(5)=3+j4. 2)Тригонометрическая: 3)Показательная: . означает вращение вектора по кругу. Тригонометрическая форма записи явл промежуточной между алгебраической и показательной: . Перевод из показательной в алгебраическую: Перевод из одной формы записи в другую необх для того, чтобв выполнить арифметические действия: При + или – используют алгебраическую. При * или / использую т показательную.