Вопрос 13

Динамика вращательного движения АТТ. Момент силы относительно неподвижной точки и неподвижной оси вращения. Работа сил при вращении АТТ.

М оментом М силы F относительно неподвижной точки О является вектор:

,

l – плечо силы F

M – момент силы F

Момент силы относительно неподвижной оси Z – это скаляр, который является проекцией.

Если на тело действует несколько сил, то результирующий момент относительно неподвижной оси Z равен алгебраической сумме моментов относительно этой же оси всех сил:

Р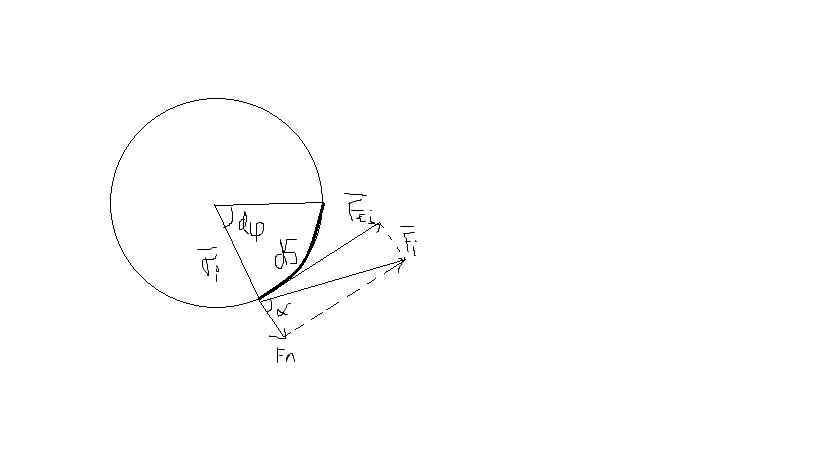 аботы сил при вращении АТТ.

Билет 14

Момент инерции системы(тела)

Момент инерции тела относительно оси вращения – физическая величина (скалярная ) равная сумме произведения масс n материальных точек системы на квадрат расстояния их до рассматриваемой оси

- момент инерции тела

-момент инерции данной точки относительно вращения

I(кг. )

При непрерывном распределении массы, сумма сводится к интегралу

Теорема Штейнера

Эта теорема определяет момент инерции тела относительно произвольной оси вращения, равен момент ее инерции относительно параллельной оси, проходящей через центр масс С:

( )

По теореме Штейнера

Кинетическая энергия вращающегося тела

Найдем ее как сумму элементарных объемов тела

Если тело одновременно участвует в поступательном и вращательном движениях причем ось вращения проходит через центр инерции (ц.м),то тела равна

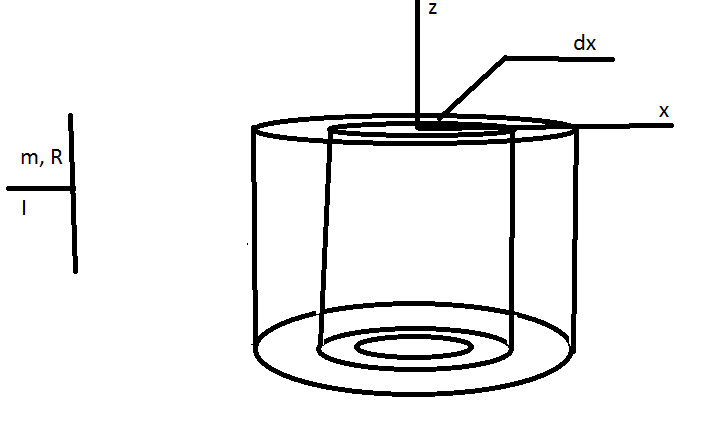
В ычесть момент инерции однородного круглого стержня длиной l и массой m, вращающегося относительно оси, перпендикулярно стержню и проходящей через один из его концов.

Вопрос 15.

Динамика вращательного движения тела. Основной закон динамики вращательного движения тела относительно неподвижной оси вращения.

Элементарная работа внешних сил действующих на вращающееся тело

Где

- основной закон динамики вращательного движения тела относительно неподвижной оси

- основной закон динамики вращательного движения относительно точки

Билет 16.

Динамика вращательного движения тела. Момент импульса, закон сохранения момента импульса.

-радиус-вектор. -импульс.

Моментом импульса относительно неподвижной оси вращения называется скалярная величина =проекции на эту ось вектора момента импульса, опред. относ. Неподвижной точки О данной оси.

Момент импульса тв. тела относительно оси есть сумма моментов импульсов отдельных точек тела.

Закон сохранения момента импульса – фундаментальный закон природы. В замкнутой системе суммарный момент равен нулю (или не действует).

Он связан со свойством симметрии пространства – его изотропность, то есть инвариантность(неизменность) физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы на любой угол)

Билет 17.

Неинерциальные системы отсчета. Силы инерции.

Это такие системы отсчета, в которых наблюдается ускоренное движение тел при отсутствии действия а них сил со стороны других тел. Причина неинерциальности систем отсчета: ускоренное движение этих систем отсчета относительно инерциальной системы отсчета.

Движение тел в неинерциальных системах отсчета: выполняется второй закон Ньютона, если формально считать, что здесь кроме реальных сил взаимодействия, существует еще так называемые силы инерции. , где F – силы инерции, а – ускорение, с которым движется система отсчета, m – масса ускоряемого тела.

- Второй закон Ньютона. Где а – ускорение тела относительно неинерциальной системы отсчета, - сумма реальных сил, действующих на тело.

Билет 18.

Гармонические колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний.

Гармонические колебания – колебания, у которых колеб. величина изменяется по закону: X=A*cos(wt+ф0), X=A*sin(wt+ф0)

X - смещение отн. положения равновесия.

A – амплитуда

Ф=(wt+ф0) – фаза колебания (рад.)

W(рад/с) – частота (циклическая, круговая)

Ф0 – начальная фаза (t=0)

Период колебаний Т – время одного полного колебания. T=t/N за время, равное периоду фазы 2π.

[w(t+T)+ф0]-(wt+ф0)=2π

wT=2π=>T=2π/w=>w=2π/T, w=2π

- число колебаний в единицу времени.

Скорость колеб. величины (первая производная от смещения):

Ускорение а колеб. величин(первая производная от скорости):

(1) – дифференциальное ур-е свободных гармонических колебаний.

Билет 19.

Механические гармонические колебания; пружинный, физический и математический маятники.

Гармонический осциллятор – система совершает колебания, описывается уравнением движения по закону .

Пр-ры: пружинный маятник. Груз m подвешен на упругой пружине жест. к и совершает колебания под действием упр. силы ( )

-kx=ma

-kx=mx’’

mx’’+kx=0

x’’+kx/m=0=> .

Физический маятник – тв. тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, не проходящей через центр масс тела.

Ур. вращ. движения:

Билет 20.

Энергия гармонических колебаний. Закон сохранения энергии свободных гармонических колебаний.