
- •Вопрос 1. Кинематика изучает движение тел, не интересуясь причинами, обусловливающими это движение
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9
- •Вопрос 10
- •Вопрос 11
- •Вопрос 13
- •Вопрос 15.
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •1.Статистический и термодинамический методы
- •Вопрос 24
- •Вопрос 25
- •29.Теплоемкость
Вопрос 8
Динамика переменной массы. Уравнение движения тела переменной массы. Уравнение Циолковского.
Выведем уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива). Пусть в момент времени t масса ракеты m, а ее скорость v; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины v+dv. Изменение импульса системы за время dt будет равно:
![]()
где u - скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:
![]()
Если
на систему действуют внешние силы,
то ![]() или dp
= Fdt.
Тогда Fdt
= mdv + udm,
или
или dp
= Fdt.
Тогда Fdt
= mdv + udm,
или
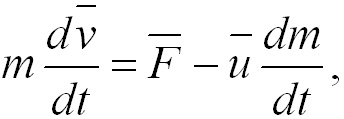 (2.12)
где
член
(2.12)
где
член ![]() называют реактивной
силой Fp.
Если вектор u противоположен v,
то ракета ускоряется, а если совпадает
с v,
то тормозится.
Таким
образом, уравнение
движения тела переменной массы имеет
следующий
вид:
называют реактивной
силой Fp.
Если вектор u противоположен v,
то ракета ускоряется, а если совпадает
с v,
то тормозится.
Таким
образом, уравнение
движения тела переменной массы имеет
следующий
вид:
![]() (2.13)
Уравнение
(2.13) называется уравнением
И.В. Мещерского.
Применим
уравнение (2.12) к движению ракеты, на
которую не действуют никакие внешние
силы. Тогда, полагая F =
0 и считая, что ракета движется прямолинейно
(скорость истечения газов постоянна),
получим:
(2.13)
Уравнение
(2.13) называется уравнением
И.В. Мещерского.
Применим
уравнение (2.12) к движению ракеты, на
которую не действуют никакие внешние
силы. Тогда, полагая F =
0 и считая, что ракета движется прямолинейно
(скорость истечения газов постоянна),
получим:

откуда
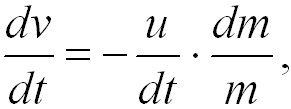
или

где С –
постоянная интегрирования, определяемая
из начальных условий. Если в начальный
момент времени v=0,
а стартовая масса ракеты составляет m0,
то C
= u*ln m0.
Следовательно,
 (2.14)
Полученное
соотношение называют формулой
К.Э. Циолковского.
Из выражения (2.14) следуют следующие
практические выводы:
а)
чем больше конечная масса ракеты m,
тем больше должна быть стартовая
масса m0;
б)
чем больше скорость истечения газов u,
тем больше может быть конечная масса
при данной стартовой массе
ракеты.
Уравнения
Мещерского и Циолковского справедливы
для случаев, когда скорости v и u намного
меньше скорости света c.
(2.14)
Полученное
соотношение называют формулой
К.Э. Циолковского.
Из выражения (2.14) следуют следующие
практические выводы:
а)
чем больше конечная масса ракеты m,
тем больше должна быть стартовая
масса m0;
б)
чем больше скорость истечения газов u,
тем больше может быть конечная масса
при данной стартовой массе
ракеты.
Уравнения
Мещерского и Циолковского справедливы
для случаев, когда скорости v и u намного
меньше скорости света c.
Вопрос 9
Работа постоянной силы. Работой
Работа – скаляр. |
Если на тело действует несколько сил (N – число сил), и вектор перемещения тела равен , то совершаемая работа равна алгебраической сумме работ, совершаемых каждой из действующих на тело сил на этом перемещении.
|
|
Работа переменной силы. Е
Рисунок 1.2.1. – Зависимость переменной силы от пути
При
бесконечно большом количестве участков,
на которое разбивается путь ( Силы, работа которых по замкнутому контуру равна нулю, называются потенциальными. В механике к потенциальным силам относятся сила тяжести и сила упругости. |
||
Работа внешних сил при вращательном движении. Полная
работа внешних сил за малое время Если
момент сил зависит от времени, т.е. |
||
Мощность. Отношение
работы к промежутку времени, в течение
которого она совершена, называется средней
мощностью N за
время Δt: Мгновенной
мощностью называется
производной по времени от работы
силы |
||
Энергия. Физическая величина, характеризующая способность тела или системы тел совершить работу, называется энергией. Формы движений в природе различны. Для количественного сравнения разных форм движений и служит понятие энергии.Механическая энергия может быть обусловлена: – или движением тела с некоторой скоростью (кинетическая энергия), – или расположением данного тела в системе других тел определенной конфигурации (потенциальная энергия). Механическая энергия равна сумме потенциальной и кинетической энергий:
|
Кинетическая энергия. Кинетической энергией тела называется энергия его механического движения. Изменение кинетической энергии тела под действием силы равно работе этой силы:
Кинетическая
энергия движущегося тела равна Кинетическая энергия механической системы равна сумме механических энергий всех частей системы. Полная
кинетическая энергия вращающегося
тела равна:
|
|
Потенциальная энергия. Потенциальная энергия – энергия, определяемая взаимным расположением тел или отдельных частей тела относительно друг друга, т.е. потенциальная энергия зависит от конфигурации системы. Соотношение,
связывающее работу потенциальной
силы с изменением потенциальной
энергии системы, имеет вид: |
||
Потенциальная энергия тяготения. Когда
тело перемещается вблизи Земли, то
говорят, что тело двигается в силовом
поле тяготения Земли
или впотенциальном
поле Земли.
Потенциальная энергия тяготения
равна: |
Потенциальная энергия упругости. В
растянутой (или сжатой) пружине на
каждую ее точку действует сила
упругости, в этом случае можно говорить
опотенциальном
поле сил упругости.
Потенциальная энергия упругости
равна
|
|
Связь между потенциальной энергией и потенциальной силой. Силы, работа которых по замкнутому пути равна нулю, называются потенциальными (или консервативными). Как указывалось ранее, в механике силы тяготения и упругости – потенциальные силы. Общая связь между потенциальной энергией и потенциальной силой: проекции потенциальной силы на оси координат равны частным производным по этим координатам от потенциальной энергии, взятым с обратным знаком:
В
определении используется понятие
частных производных, т.к. потенциальная
энергия в общем, виде зависит от трех
координат |
||
Связь работа и энергии. Работа – мера изменения энергии(физический смысл работы). Теорема о кинетической энергии: работа всех сил приводит к изменению кинетической энергии теле (или системы тел)
Работа потенциальной силы, приводящая к изменению конфигурации системы, равна приращению потенциальной энергии, взятому со знаком минус:
|
||

 .
. .
. сли
рассматриваемый участок траектории
разбивается на большое число
сли
рассматриваемый участок траектории
разбивается на большое число .
. ,
гдеm –
масса тела,
,
гдеm –
масса тела,  .
Если тело не движется, его кинетическая
энергия равна нулю.
.
Если тело не движется, его кинетическая
энергия равна нулю. ,
где
,
где  ,
где х –
изменение длины растянутой пружины,
отсчет х ведется
от положения равновесия, в котором
,
где х –
изменение длины растянутой пружины,
отсчет х ведется
от положения равновесия, в котором  ;
;