2.1.Интегральная и дифференциальная функции распределения. Вероятность попадания в заданный интервал.
Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях.
Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой зависимости). При соблюдении некоторых не очень жестких условий указанная сумма случайных величин подчиняется приближенно нормальному закону распределения и тем точнее, чем большее количество величин суммируется.
Ни одна из суммируемых случайных величин не должна резко отличаться от других, т. е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию.
Для примера рассмотрим изготовление некоторой детали на станке-автомате. Размеры изготовленных деталей несколько отличаются от требуемых. Это отклонение размеров от стандарта вызывается различными причинами, которые более или менее независимы друг от друга. К ним могут относиться:неравномерный режим обработки детали; неоднородность обрабатываемого материала; неточность установки заготовки в станке; износ режущего инструмента и деталей станков; упругие деформаций узлов станка; состояние микроклимата в цехе; колебание напряжения в электросети и т. д. Каждая из перечисленных и подобных им причин влияет на отклонение размера изготовляемой детали от стандарта. Таким образом, общее отклонение размера, фиксируемое измерительным прибором, является суммой большего числа отклонений, обусловленных различными причинами. Если ни одна из этих причин не является доминирующей, то суммарное отклонение является случайной величиной, имеющей нормальный закон распределения.
Так как нормальному закону подчиняются только непрерывные случайные величины, то это распределение можно задать в виде плотности распределения вероятности.
Определение: Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид
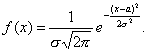
8.Вероятность попадания в заданный интервал нормальной случайной величины.
Нормально распределенные непрерывные случайные величины встречаются в практических задачах чаще всего. Это связано, в частности, с Центральной предельной теоремой Ляпунова, которая утверждает, что если случайная величина порождена несколькими примерно равными по силе причинами, то она становится нормально (или почти нормально) распределенной. Плотность (дифференциальная функция) нормального распределения равна
,
т.е. зависит
от двух параметров: математического
ожидания a и
среднего квадратического отклонения .
Интегральная функция нормального
распределения связана с функцией
Лапласа
, значения которой
берутся из таблиц (см.ниже). Для вычисления
вероятности того, что нормально
распределенная случайная величина X
будет принимать значения в
промежутке используется
формула
9. Каждая случайная величина полностью определяется своей функцией распределения.
В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.
Математическое ожидание случайной величины
Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .
Математическое ожидание дискретной случайной величины x , имеющей распределение
x1 |
x2 |
... |
xn |
p1 |
p2 |
... |
pn |
Математическое ожидание непрерывной случайной величины с плотностью вероятностей px(x) вычисляется по формуле . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.
Если случайная величина h является функцией случайной величины x , h = f(x), то
Основные свойства
математического ожидания:
математическое ожидание константы равно этой константе, Mc=c ;
математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и bсправедливо: M(ax + bh ) = a M(x )+ b M(h );
математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).
Дисперсия случайной величины
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )2.
Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.
Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам
10.Схема повторных испытаний. Формула Бернулли. Предельные теоремы в схеме Бернулли (Пуассона, Муавра-Лапласа).
Формула Бернулли
Если при одних и тех же условиях определенный опыт повторяется n раз и если вероятность появления некоторого события А в каждом опыте равна р, то вероятность того, что событие А в серии из n опытов произойдет ровно к раз, находится по формуле Бернулли:
Сочетания
из n по к находят по формуле
Число к появлений события А в серии из n опытов, вероятность которого наибольшая, называется наивероятнейшим числом наступления события А в n опытах. Это число находят по формуле
к = [np + р]. (2)
Символ [...] означает здесь целую часть числа.
Если число np + р - целое, то наивероятнейшим будет также и число к0 - 1 с той же вероятностью Pn (к0).
Пример 6.15. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две детали будут нестандартными. Каково наивероятнейшее число нестандартных деталей в рассматриваемой выборке из 30 деталей и какова его вероятность?
Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - появление нестандартной детали; его вероятность Р = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли находим:
P30 (2) = C0 (0,04)2 (0,96)28 » 0,202.
Наивероятнейшее число нестандартных деталей в данной выборке вычисляется по формуле (2):
к0 = [30 ¦ 0,04 + 0,04] = [1,24] = 1, а его вероятность равна
P30(1) = C1c • 0,041 • (0,96)29 » 0,305.
Пример 6.16. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность того, что в серии из четырех выстрелов будет: а) хотя бы одно попадание; б) не менее трех попаданий; в) не более одного попадания.
Решение. Здесь n = 4, p = 0,8, q = 0,2. а) Найдем вероятность противоположного события - в серии из четырех выстрелов нет ни одного попадания в цель:
Отсюда находим вероятность хотя бы одного попадания в цель:
б)
Событие В, заключающееся в том, что в
серии из четырех выстрелов произошло
не менее трех попаданий в цель, означает,
что было либо три попадания (событие
С), либо четыре (событие D), т. е. В = С + D.
Отсюда P (B) = P (C) + P (D); следовательно,
в) Аналогично вычисляется вероятность попадания в цель не более одного раза:
