Назначение, конструкция, расчет передач

При необходимости передачи момента между валами, геометри­ческие оси которых пересекаются, применяют конические фрикцион­ные передачи (см. рис. 11,3). Угол пересечения осей валов может быть любым, однако практи­чески наибольшее распрост­ранение имеют конические фрикционные передачи, оси валов которых пересекаются под углом 90° (рис. 15):

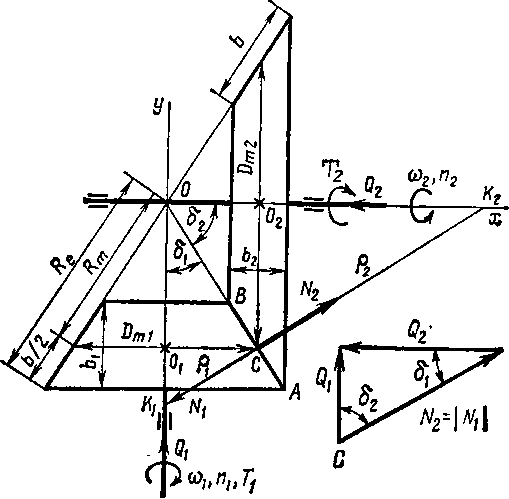
г^+б^эо⁰.

При конструировании ко­нических фрикционных пере­дач необходимо обеспечить точность пересечения осей валов и общей образующей OA конических поверхностей катков в одной точке О. Не­соблюдение данного условия вызывает так называемое гео­метр ическое скол ьжен ие* _f

КОТОрое ПРИВОДИТ К быстро- Рис. 15

му и неравномерному изно­су рабочих поверхностей катков.

Передаточное отношение конической передачи

i = = njn₂ = D_m2/D_ml = tg 8₂ (26)

[из AC00₂ (рис. 15) tge_e = 0_f6D_e8/(0_f5D_el) = t].

Среднее конусное расстояние

R_u = V(0,5D_Ml)* + (0,5Р„_а)' - У(Ъ£Р_т1? + (0>ЫР_а1)* =

R_u = 0,SD_MlVi^% + L (27)

Конусное расстояние

R_e = R_m + b/2, (28)

* Скольжение названо геометрическим потому, что оно обусловлено лишь геометрией катков и не зависит от силы сжатия Q,

В приведенных формулах D_mi = 2RjVi² + 1 — средний диаметр ведущего катка; -ф_Я| = 6//?_1Я = 0_>22.. .0,29 —коэффициент ширины кат­ков; b = ty_mR_m <с:о_т1 — длина линии контакта (или ширина катков, измеренная вдоль образующей конусов).

2 К* 2484

33

Физическая и техническая сущность г|)_от аналогична я|) (см. заня­тие 2).

Передача момента к ведомому валу осуществляется силами тре­ния, возникающими между рабочими поверхностями катков благо­даря действию силы нормального давления, обусловленной осевой силой сжатия Q_f на ведущем катке (или Q₂ на ведомом катке).

Сила нормального давления N, приложенная в точке С контакт­ной линии на окружности среднего диаметра катков, может быть выражена через осевые силы Q_t и Q₂. Из силового треугольника (рис. 15) получаем

^^r₁ = Q₁/sin 6_Л и N₂ = Q₂/sin6₂. (29)

Определим требуемые значения сил Q_t и Q₂ с учетом коэффи­циента сцепления (нагрузки) /С. Сила трения

Fj-fN^KFt-WTjD.i;

используя формулы (29), получаем

Q_t = 2KT_t sin WDni), (30)

Q₂ = 2KT₂sinWD_m2). (31)

Прижатие одного катка к другому обеспечивается пружиной, установленной на валу ведущего (малого) катка, так как Qi<Q₂ (при t>l), и нажимающей на торцовую поверхность ступицы, свободно насаженной на шлицевой вал или на вал с направляющей шпонкой. В зависимости от конструкции нажимная пружина может быть установлена и на ведомом валу (см. рис. 10).

Расчет фрикционной конической передачи основан на тех же предпосылках и аналитических зависимостях, что и цилиндрической.

Для катков, материал которых подчиняется закону Гука, расчет ведут на контактную выносливость. При проектировочном расчете определяют среднее конусное расстояние по формуле

R_m^VW+i /(0,418/К])«KT^/WJ). (32)

Для проверочного. расчета (проверки контактной выносливости) служит формула

^{ая = (0,418//?J У KT^ViP + lTKfbiX [ан]. (33)}

Единицы в этих формулах те же, что и при расчете цилиндри­ческих фрикционных передач.

Рассмотрим вывод формул (32) и (33). Для этого сделаем соответствующие подстановки в формулу (21а), используя условие о_н*^[о_И] и ранее полученные аналитические зависимости.

За радиус кривизны катков принимаем отрезок перпендикуляра к общей обра­зующей боковых поверхностей катков ЛВ (рис. 15), проведенный из середины АВ до пересечения с геометрической осью катка:

pi — CKi — Rm ctg 6_а = R_m; • 1/tg 6₂ = R_m • 1/t —радиус кривизны ведущего катка, р₂ = С/Сг = Rm *g Ой = Rmi—радиус кривизны ведомого катка,

Приведенный радиус кривизны катков (см. занятие 2)

_ Plp2 (Rm/i) Rm _ Rmi

^Pnp~~Pl+p₂~ (RmH) + Rm '

Заменив в формуле (21a) Q, см. формулу (30), D_m\, см. формулу (27), 6 = "Фот^от и р_пр, получим

a*=0,418"|/ ^=0,418^ / 7_Р"'^ух" ' <[а_я[,

или

м р р» - ^<[а//1> Возведя в квадрат неравенство (а), получим

0,418* "⁽²⁾

^Р _р <[*дЕ.

Решая последнее уравнение относительно R_m, получаем формулу (32). Заменив в неравенстве (a) ty_mR_m = b_t получим формулу (33) для проверочного расчета.

Если материал катков не подчиняется закону Гука (кожа, ре­зина, дерево и др.), то расчет конической фрикционной передачи ведут на износостойкость по погонной нагрузке:

_q=Nib=ад/с_в1)=КТ_г VF+ll(bfR_m), откуда следует формула для проверочного расчета

q =КТ_г VlH^lWJ < fob (34)

Подставив сюда b=^^_mR_m9 получим формулу для проектировоч­ного расчета:

Я_т>/ КТ_гУ 1²+1/(/Ы<7])- (35)

Последовательность проектировочного расчета:

1. Определяем крутящий момент на валу ведущего катка по формуле (15):

2. Находим углы конусности катков:

б₂ = arctg f и б₁ = 90° —б₂.

3. По формуле (32) или (35) находим среднее конусное расстоя- ние, выбрав предварительно материалы катков и найдя соответствую- щие значения / и [а_И] или [q]. Задаемся величинами К и

23. По формулам (27) и (26) вычисляем средние диаметры катков.

24. Уточняем R_m и вычисляем b и R_e.

25. Определяем ширину катков в осевом направлении (рис. 15):

= cos 8_г\ b₂ = 6cos6₂. (36)

²* 35

Краткие сведения о вариаторах

Передачи, обеспечивающие плавное, бесступенчатое изменение угловой скорости ведомого вала при неизменной угловой скорости ведущего, называют вариаторами.

На рис. 16, а показан лобовой фрикционный вариатор. При воз­растании х (рис. 16, б) увеличивается длина окружности, которую описывает точка вращающегося ведомого катка А на поверхности диска В, что и приводит к уменьшению угловой скорости со₂ ведо-

Рис. 16 Рис. 17

и 3 и промежуточным цилиндрическим катком 2, зажатым между коническими катками с помощью пружины 4. При вращении махо­вика 5 винт 6_У перемещающийся в подшипниках 7, передвигает про­межуточный каток 2, свободно вращающийся на оси винта. При постоянной угловой скорости ведущего катка / значение угловой скорости ведомого катка 3 изменяется. Если промежуточный каток 2 перемещается влево, то угловая скорость ведомого катка 1 увели­чивается.

На рис. 18 показана схема вариатора В. А. Светозарова с соосным расположением осей валов. Сферические катки 1 и 2 насажены на ведущий и ведомый валы передачи. Ролики 3 и 4, прижимающиеся к сферическим поверхностям катков, выполняют роль промежуточ­ного катка. При поворачивании роликов вокруг своих осей (штри­ховыми линиями показано одно из возможных положений роликов) происходит плавное изменение ведомого вала.

Кинематической характеристикой вариатора служит диапазон регулирования Д, представляющий собой отношение наибольшей угловой скорости (частоты вращения) ведомого вала к его наимень­шей угловой скорости (частоте вращения):

Д ⁼⁼⁰⁾ 2 тахА°2 min = ^П2 max/#2 min- (37)

Кроме фрикционных вариаторов в машиностроении применяют ременные и цепные вариаторы.

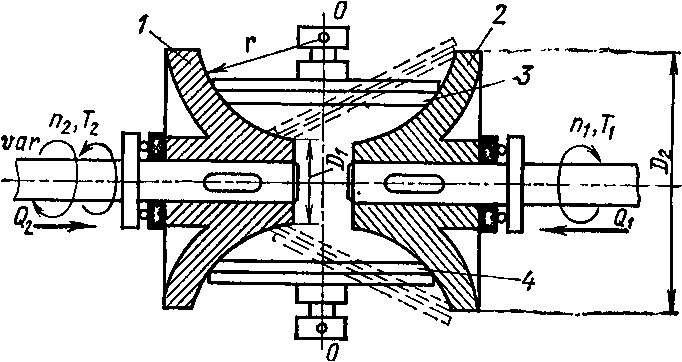
Рис. 18

Задача 5. Для конической фрикционной передачи, геометрические оси которой пересекаются под прямом углом, вычислить передаточное отношение, угловую скорость ведомого вала, линейную скорость на окружности средних диаметров катков, средние диаметры катков, их ширину и конусное расстояние, если: а) Я я, = 250 мм, 6i = 20°20', л_х = 735 мин-*; б) R_m = 320 мм, 6i = 21^o30', п_г = = 970 мин-¹.

Решение, а) 1. Вычерчиваем кинематическую схему передачи (см. рис. 15).

2. Определяем угол конусности ведомого катка:

6₂ = 90°—6i = 90°—20°20' = 69°40'.

3. По формуле (26) находим передаточное отношение и частоту вращения ведомого вала:

/ = tg6₂ = tg69°40' = 2,7; ==735/2,7 = 272 мин-».

4. По формуле (27) вычисляем средний диаметр ведущего катка:

D_ni = 2R_m/ = 2• 250/ У 2,11 -f 1 = 500/2,88 » 174 мм,

5. По формуле (26) определяем средний диаметр ведомого катка:

D_OT2 = iD^i = 2,7-174 = 470 мм.

6. Вычисляем линейную скорость на окружности средних диаметров катков:

v_m = = я• 174«10- ³.735/60 = 6,68 м/с.

7. Назначаем значение коэффициента длины общей Образующей катков и вы- числяем ее длину.

Из ty_m = b/R_m = 0,22.. .0,29, принимая ^_т =b/R_m = 0,25, получаем Ь = = 4\лЯт = 0,25-250 = 62,5 мм.

Принимаем 6 = 63 мм, расчетное значение Ь следует округлить до целого числа,

8. По формуле (28) определяем конусное расстояние:

Л« = /?_Л+0₁5&=250+0,5«63 = 281,5 мм.

9. По формуле (36) находим ширину ведущего Ь\ и ведомого Ь₂ катков в на­правлении осей валов:

Ь_х = b cos 61 == 63 cos 20°20' = 63-0,938 = 59,2 мм, b₂ = b cos 6₂ = 63 -cos 69°40' = 63.0,347 = 21,85 мм.

Задача 6. Рассчитать коническую фрикционную передачу, если:

_а) Р₁₌=3 кВт, Их = 950 мин"^-1, «2 = 350 мин"^-1; материал катков: 1) чугун —

текстолит, 2) чугун —резиновая обкладка; б) Р_х=1,7 кВт, п₂ = 400 мин"^-1, t = 2,5;

материал катков: 1) чугун—сталь, 2) чугун—кожа.

Решение, а) Проектировочный расчет. 1. Определяем передаточное отношение

по формуле (26):

i = щ/п₂ = 950/350 = 2,71.

2. По формуле (26) находим углы конусности:

tg6₂ = t = 2,71 и 6₂ = arctg2,71=69°44\ 6_t = 2 — б₂ = 90°—69°44' = 20° 16'.

3. Вычисляем крутящий момент на ведущем валу:

Tf = 9,55Pi/n = 9,55• 3 • 10³/950 = 31,6 Н • м.

4. По формуле (32) вычисляем среднее конусное расстояние. Принимая по табл. П2 модули упругости материала катков—чугуна £i = £_4yr = 1,2» 10¹¹ Па; текстолита E₂ = E_ltKCT = 7* 10⁹ МПа,—находим приведенный модуль упругости катков:

£_пр = 2E₁E₂/(E_i+ Е₂) = 2-1,2- 10^п.7.10»/(1,2- 10ⁿ+7-10⁹) = 13,22-10» Па.

Коэффициент нагрузки К— 1,2... 1,5, принимаем /С=1,5.

Так как для чугуна [о_н] « 1,5ст_ви (о_ви—см. табл. ПЗ) значительно больше, чем для текстолита [о_н] = 50... 100 МПа, то расчет следует вести по наименьшим допускаемым контактным напряжениям, т. е. принимаем для текстолита расчетное [а_я] =80 МПа.

Находим: ty_m = b/R_m = 0,22.. .0,29, принимаем if^ = 0,25;

/ = 0,2...0,25 (см. табл. Ш), принимаем / = 0,2.

Следовательно,

_г ³ Г( 0,418 \2 KT_tE_nv

- VTn^S/(MlLY . 1.5-31,6-13,22-10» yj^T_Q=s

-hi у ^ 80.10V 0,2.0,25-2,71 ^А^*^ш ^

= 0,143 м=143 мм.

Принимаем для катков чугун—текстолит i?_w = 145 мм. Для катков чугун—резина R_m вычисляем по формуле (35):

[q] = (9,8...29,5) 10³ Н/м (см. табл. П4), принимаем [</] = 18.10³ Н/м; / = 0,35.. .0,45 (см. табл. Ш), принимаем / = 0,4. Следовательно,

*"^|/ ЛЫ?1 "У 0,4.0,25.18.10³ — Г ⁷»^26.1° -0,269 м. Принимаем R_m = 270 мм.

5. Определяем средние диаметры катков по формулам (26), (27). Для катков чугун—текстолит

D_mi = 2RjY = 2.145/^2,71²+1 =290/2,89 » 100 мм, Ая2 = Щя1 = 2,7Ы 00 = 271 мм. Принимаем D_wi=100 мм* £>_да2 = 270 мм,

Уточняем передаточное отношение и среднее конусное расстояние: * = Р«,₈/Р«1=* 270/100 = 2,7; R_m = 0,SD_mi j/*2+1=0,5-100 ]/2jI+1 = 144 мм. Для катков чугун—резина

D_mi = 2Rj }П*+Т = 2 ■ 270/ /2,71 ? +1 = 187 мм,

принимаем D_wi = 190 мм;

Ая2=='£>/я1== 2,71.190 = 515 мм.

По формулам (26), (27) уточняем передаточное отношение и среднее конусное расстояние:

i = D_m2/D_mi — 515/190 = 2,71 — не изменилось; R_m = 0,5D_mi 1^71+1 = 0,5.190 1/2,71*+ 1 = 274 мм.

6. Определяем длину общей образующей, ширину катков—по формуле (36) и конусное расстояние—по формуле (28):

1) & = ih»tf_w = 0,25.144 = 36 мм;

b!==b cos 6i = 36 • cos 20° 16' = 36 • 0,938 = 38,8 мм; b₂ = b cos S₂ = 36.cos 69°44' = 36 -0,347 =12,6 мм; R_e = Rm + № = 144+0,5-36= 162 мм;

2) b — T\)_mR_m = 0,25'274 = 68,5 мм, принимаем 6 = 70 мм;

b_t = b cos 6i = 70-0,938 = 65,6 мм; b₂ = bcos б₂ = 70-0,347 = 24,3 мм; /?e = /?« + 0,56 = 274+0,5.70 = 309 мм.

7. Полагая, что нажимным является малый (ведущий) каток, по формуле (30) находим осевую силу сжатия:

^{!) Ql=}Wi ^Sl" ^б1= 0,2.10⁵0³Ш⁶-_а ^{Sin 2}°°¹⁶' - ¹⁵⁷⁰ "! 2) Q,«$± sin б_{1= Q} ²;.''₉⁵₀У._а sin 2046' ^412 Н.

Задача 7. Вычислить наименьшую и наибольшую частоты вращения ведомого вала и диапазон регулирования фрикционного вариатора с усеченными конусами (см. рис. 17), если: а) /^ = 730 мин"¹, d_A==do~^0 мм, d_B = dc = 120 мм; б)" п_г = = 480 мин-*¹, d_A=df) = 50 мм, d_B = d_c = 20Q мм.

Решение, а) 1. Частота вращения ведомого катка 1 зависит от положения промежуточного катка 2, свободно вращающегося на оси и зажатого между обра­зующими боковых поверхностей конических катков. Если каток 2 переместить в положение Л С, то частота вращения ведомого вала катка 1 станет наибольшей; при перемещении катка 2 в положение BD частота вращения катка 1 Судет наи­меньшей.

2. По формуле (18) определяем передаточное отношение вариатора, также наименьшую и наибольшую частоты вращения ведомого вала (см. рис. 17):

а) при положении BD катка 2

*>BD max = «i/«2 = d_B/d_D = 120/40 = 3

и

n₂ = n_x/i_BD = 730/3 = 243, мин~^l^n_{2 min};

б) при положении AC катка 2

Mс min = лх/яа = d_Afd_c = 40/120 = 0,333

и

п₂ = n₁/i_AC = 730/0,333 = 2190 мин"¹ = п_{2 тах}.

3. По формуле (37) находим диапазон регулирования вариатора:

Д = п_{2 max}//i2 min = 2190/243 = 9,01.

Очевидно, диапазон регулирования вариатора можно найти и через отношение его экстремальных передаточных отношений:

Д = iBD/Uc= 'maxA'mln = 3/0,333 = 9,01. Литература: [3,6,8,11]; задачи 7.7,7.9,7.14 [12].

Вопросы для самопроверки. 1. Укажите причины необходимости применения передач в машинах. 2. Как классифицируют механические передачи? 3. Сформу­лируйте определение вращательного движения тела относительно неподвижной оси и приведите примеры деталей и сборочных единиц машин, находящихся во вра­щательном движении. 4. Каково взаимное направление вращения и момента дви­жущих сил Т±, а также вращения и момента сил сопротивления Т₂ при передаче энергии от ведущего вала к ведомому? 5. Сформулируйте определение передаточ­ного отношения. Чему равно передаточное отношение ременной передачи, если ведущий шкив вращается с угловой скоростью o)i=150 рад/с, а ведомый—с (о₂ = = 100 рад/с? 6. Вычислите КПД ременной передачи, если i=4, 7\=100 Н»м, 7^ = 380 Н'М. 7. Вычислите окружную скорость фрикционного катка, если п = = 400 мин~⁴, Z> = 600 мм. 8. Укажите достоинства и недостатки фрикционных передач. 9. Какие требования предъявляют к материалам рабочих поверхностей фрикционных катков? 10. При каких значениях передаточного отношения ведомый вал вращается: а) с той же скоростью, что и ведущий, б) медленнее, в) быстрее?

26. Укажите нажимные устройства, применяемые во фрикционных передачах.

27. Почему при выполнении расчета фрикционных передач с катками, рабочие поверхности которых изготовлены из неметаллических материалов, нельзя приме­нять формулу (21) и основанные на ней расчетные формулы? 13. Для чего в рас­четные формулы вводят коэффициент нагрузки? 14. Какое оказывает влияние •ф (\|),_л) на габариты передачи и размер окружной силы? [См. занятие 2; рис. 13 и формулы (22), (25), (32), (35)]. 15. От чего зависит межосевое (среднее конус­ное) расстояние фрикционной передачи? [См. формулы (22), (25), (32), (35)]. 16. Зависит ли сила нажатия от коэффициента трения и если да, то как? От чего еще и как зависит эта сила? 17. Какую фрикционную передачу называют вариа­тором? 18. Наименьшая угловая скорость ведомого вала вариатора co_2mi_n= 10 рад/с, диапазон регулирования Д = 4. Какова наибольшая угловая скорость ведомого вала?