Волновые передачи

Передачи, в которых преобразование движения осуществляется за счет перемещения волны деформации гибкого звена, называются волновыми. Механические волновые передачи могут быть фрикцион­ными, резьбовыми (винт—гайка) и зубчатыми.

Перемещение волны деформации гибкого колеса 1 (рис. 138) зубчатой волновой передачи (фрикционные и резьбовые волновые передачи еще не получили распространения и здесь не рассматри­ваются) вызывается подвижным механическим (или немеханическим, например электромагнитным) устройством 2, называемым генера­тором волн. Замыкает кинематическую цепь волновой передачи

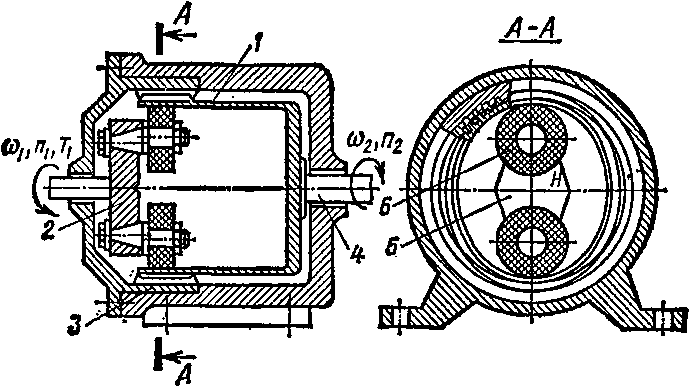
Рис. 133

(для краткости слово «зубчатой» опускаем) звено 3 —неподвижное жесткое зубчатое колесо с внутренними зубьями. Гибкое колесо / выполнено в виде упругого тонкостенного стакана с внешними зубьями z₂, нарезанными на поверхности венца (утолщения) откры­той части стакана; закрытый торец стакана жестко соединен с ве­домым валом 4. Генератор волн 2 состоит из водила 5, жестко соединенного с ведущим валом (®_i9 я_х), и двух вращающихся роли­ков 6, закрепленных на эксцентриковых осях, позволяющих регу­лировать ролики в радиальном направлении.

Так как делительный диаметр гибкого колеса d₂ меньше дели­тельного диаметра жесткого колеса d₃, то ролики генератора дефор­мируют гибкое колесо, придавая ему форму эллипса (см. разрез Л —Л на рис. 138). При этом у концов большей (вертикальной) оси эллипса зубья колес находятся в полном зацеплении, а в на­правлении к концам меньшей (горизонтальной) оси эллипса радиаль­ный зазор между зубьями колес увеличивается и в зонах, примы­кающих к концам этой оси, зубья колес полностью выходят из зацепления.

При работе описанного генератора возникают две движущиеся волны (двухволновой генератор) гибкого колеса, вызывающие в нем радиальное и угловое перемещение; гибкое колесо обкатывается по неподвижному жесткому колесу в направлении, противополож­ном вращению вала генератора.

Из-за большой многопарности зацепления (например, в зацепле­нии пары колес двухволновой передачи одновременно находится 25... 30% зубьев гибкого колеса) волновая передача позволяет существенно повысить плавность зацепления, несущую способность и кинематическую точность.

На рис. 139 показан одноступенчатый волновой редуктор. Гене­ратор волн 5 представляет собой жесткий кулачок, связанный с ве­дущим валом 1 упругой резиновой муфтой 14, предназначенной

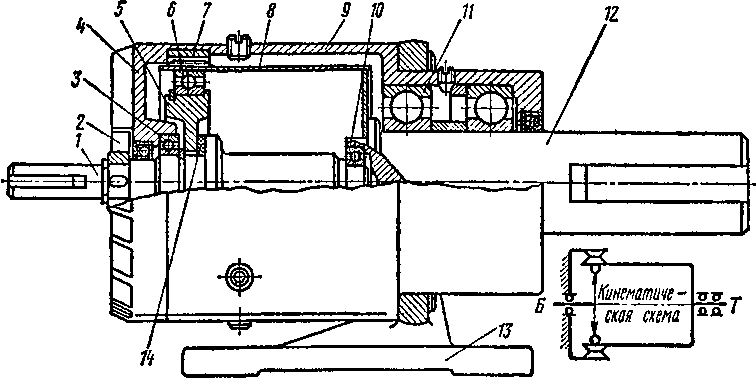
Рис. 139

для равномерного распределения нагрузки по двум зонам зацепле­ния. Между кулачком и деформированным гибким звеном распо­ложен шарикоподшипник 6 с гибкими деформируемыми обоймами. Гибкое колесо 8 выполнено в виде упругого тонкостенного стакана с приваренным дном, жестко связанным с ведомым валом 12. Жесткое колесо 7 с внутренними зубьями крепится к левой крышке 4_% в которой расположена опора 3 ведущего вала 1\ вторая опора 10 расположена внутри ведомого вала 12. В правой части корпуса 9 расположены два подшипника 11 тихоходного вала. К корпусу прикреплен кронштейн 13 с лапами для крепления редуктора. Для увеличения теплоотдачи на быстроходный вал надета крыльчатка 2, а на крышке корпуса (со стороны генератора волн) имеются радиаль­ные ребра.

Техническая характеристика редукторов, выпускаемых по конст­руктивной схеме рис. 139: и « 80 ... 300, Р « 0, 05 ... 3 кВт, г\« «0,75 ... 0,90.

Волновые передачи могут быть использованы для передачи вра­щения в герметизированное пространство через непроницаемую стенку, без применения уплотнений или специальных диафрагм. На рис. 140 показана конструкция такой передачи. На валу электро­двигателя 1 закреплен двухволновой генератор 2 о промежуточ­ными телами качения (шариками). Для уменьшения напряжений в зоне наибольшей деформации гибкое колесо 3 изготовлено слож­ной формы с жестко закрепленными торцами. В средней части гибкое колесо имеет наружные зубья, находящиеся в зацеплении с зубьями жесткого колеса 4, выполненного в виде свинчиваемых полуколец. Область внутри гибкого звена герметична и изолиро­вана от окружающего пространства. Это и позволяет использовать передачу в приводах космических кораблей и изолированных хими­чески агрессивных сред.

Достоинства. 1. Большая несущая способность на единицу массы передачи (в 3... 4 раза выше зубчатых передач). 2. Воз­можность получения больших передаточных отношений до 1000 в одной ступени передачи. 3. Плавность и бесшумность работы передачи. 4. Высокая кинематическая точность передачи. 5. Надеж­ность зацепления (при многопарном зацеплении поломка зуба не

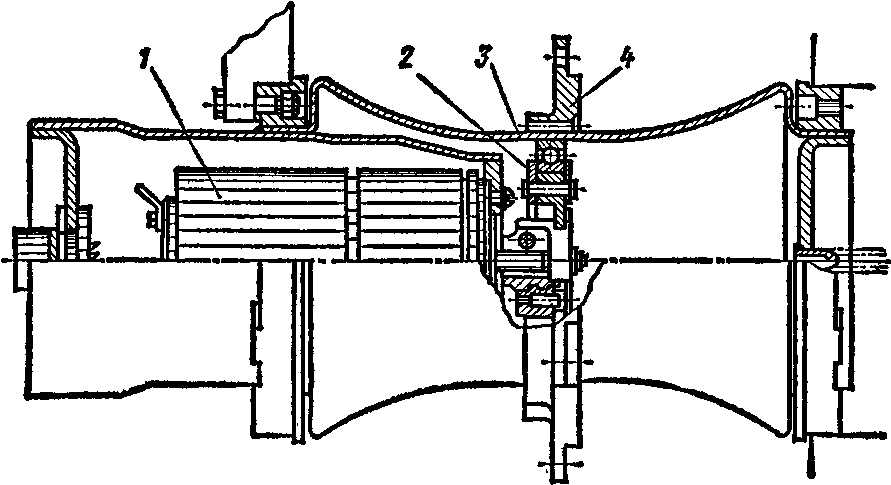
Рис. 140

нарушит работоспособности и точности передачи). 6. Возможность передачи движения в герметизированное пространство. 7. Малогаба-ритность и возможность рационального использования объема передачи при ее компоновке.

Недостатки. 1. Сложность конструкции генератора волн. 2. Не­обходимость выбора оптимальной геометрии зубьев колес. 3. Из-за непрерывного значительного деформирования гибкого колеса пред­ставляют повышенные требования к выбору его материала (сталь, пластмасса) и технологии изготовления. 4. Маломощность передачи (до 3.. .5 кВт). 5. Невысокий КПД (в силовых передачах г] = 0,75... ...0,90).

Несмотря на указанные недостатки, область применения передач расширяется. Одноступенчатые и многоступенчатые волновые пере­дачи применяют в силовых и кинематических автономных или встроенных редукторах и мультипликаторах при /_л,₆=50... 105; в башенных строительных кранах; в приводах космических аппа­ратов; в уникальных механизмах различного типа летательных ап­паратов, луноходах, атомных реакторах, приводах прецизионных приборов и др.

Так как волновые передачи изобретены недавно (В. Мессером в 1959 г.), то установившейся геометрии и методики их расчета пока не существует. При расчете обычно используют следующие формулы (рис. 141).

Делительные диаметры гибкого d₂ и жесткого d_u колес опреде­ляют, как и в зубчатых передачах:

d₂ = mz* или do = mz«.

(178)

Разность делительных диаметров жесткого и гибкого колес

d_a — d₂ = mi_T = A_3t2, (179)

где *_г — число волн генератора (обычно *'_г = 2); Д_{3в 2}—- приращение делительных диаметров жесткого и гибкого колес.

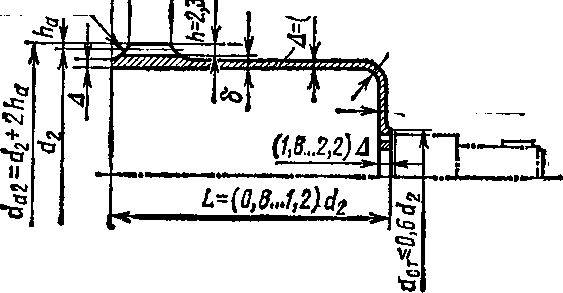
Д иаметры вершин зубьев:

гибкого колеса

d_a2 = d₂ + 2x₂m; (180) жесткого колеса d_a3 = d₃—2(f_Q — х₃)т, (181)

где /₀—коэффициент вы­соты головки зуба, х— коэффициент смещения исходного контура при нарезании зубьев гиб­кого х₂ и жесткого х_в колес. Значения указан­ных величин зависят от

многих факторов (а, z, т и др.) и принимаются по специальным рекомендациям (см.* например, [2]). Передаточное отношение

j (£l tti _j

^— щ ^— л₂ ^3 "

Окружная скорость

*3 ,2

#3 — #2 /r

(182)

0=(o₂d₂/2 = nd₂n₂/60.

Момент на валу генератора Т± вычисляют по известной форму­ле (17), где Т₂ — момент на ведомом валу (гибком колесе). При установившемся равномерном вращении валов передачи

7\ + Г₂ + Г₃ = 0, где Т_а —-момент, приложенный к жесткому колесу.

Расчет планетарной и волновой передач

Последовательность силового и геометрического расчета плане-тарной передачи зависит от условий ее эксплуатации. При отсут­ствии ограничения габаритных размеров передачи ее силовой и геометрический расчет выполняют аналогично расчету обыкновен­ных зубчатых передач с учетом геометрии внутреннего зацепления.

Передаточные отношения зависят от схемы передачи.

Если передачу необходимо вписать в заданные габариты, напри­мер в корпус станка или двигателя, то диаметр центрального колеса (колеса k с внутренними зубьями, см. рис. 135) принимают в соот­ветствии с допускаемыми размерами, т. е., выбрав числа зубьев колес (см., например, с. 101 [2]) и вычислив передаточное отноше­ние, по формуле (83) определяют модуль зацепления, а по форму­ле (87) —межосевое расстояние, которое для колес внутреннего зацепления

о*=* (d,-di)/2- (т/2) (г^г^ (тг_£/2) (I-1). (183)

Диаметр вершин зубьев колеса

d_tf2 = d₂—2m+15,2 т[г_й. (184)

Диаметр впадин зубчатого колеса k

d_/a = d₂ + 2,5 m. (185)

Ширина венца Ь зубчатого колеса может быть найдена по фор­муле (90) при 1—1 для внутреннего зацепления.

Окружная сила в планетарной передаче (см. рис. 135)

Ftt = Fn = 2KnTi/(tA)> (186)

где К_н — 1,1.. .2 —коэффициент, учитывающий неравномерность рас­пределения нагрузки между сателлитами; i_c — число сателлитов; Т±— момент, передаваемый шестерней b (см. рис. 135); ^—дели­тельный диаметр шестерни Ь.

Для зубчатых колес внутреннего зацепления коэффициент формы зуба можно вычислить по приближенной формуле

Y_FH&2z/(z + 20). (186а)

Кинематический расчет любой планетарной передачи рекомен­дуется выполнять в такой последовательности:

76. Мысленно закрепляем все колеса на водиле Н и получаем одинаковую угловую скорость колес и водила—о_я.

77. Мысленно закрепляем водило (т. е. планетарную передачу превращаем в зубчатую) и поворачиваем центральное колесо с уг­ловой скоростью со, равной разности абсолютных скоростей водила и центрального колеса, но в обратную сторону вращения водила:

0)=^ — —©_ц).

3. Последовательно складывая угловые скорости, полученные в первом и втором движениях звеньев передачи, находим угловую скорость каждого звена (колеса, водила).

Последовательность расчета волновой передачи.

1. По наиболее нагруженному зубу определяют модуль

т>//СГЖ'Ч> [*«.]). (187)

где К —коэффициент, зависящий от типа генератора. Например, при двухволновой передаче (*_г = 2)/(= 11,6 для кулачкового (при а = 20°), К =18,5 для дискового, /( = 36,2 для роликового генера­тора; t|>==&/d₂ = 0,07.. .0,12 —коэффициент длины зуба; [а_см]= = 350.. .500 МПа—допускаемое напряжение смятия для сталей 40Х, ШХ15, 35ХГСА, 38ХМОА и др., применяемых для изготовления гибкого крлеса твердостью НВ250...350.

78. По формуле (182) вычисляют передаточное отношение и, пред­варительно задавшись числом волн i_r (обычно £_г = 2), определяют *₂ = п_г.

79. Используя формулы (178), (179), находят число зубьев жест­кого колеса г₃ = г₂-Ы_г.

80. С помощью формул (178) определяют d₂ и d₉.

81. Вычисляют длину зуба:

6 = t|)d_a. (188)

6; Проверочный расчет выполняют из условия прочности зубьев на смятие

Ос* = КТ№Ыт*)^[о_сы] (189)

и из условия прочности гибкого колеса на кручение

т_к = 2^_tT₂/(nXdl) < [т_к], (190)

где i|)_f = d/A = 80... 100 — отношение диаметра трубы d к тол­щине ее стенок А (см. рис. 141); X = 1/6— коэффициент неравно­мерного распределения касательных напряжений по периметру гиб­кого колеса; [т_к]« 50...80 МПа.

82. По формулам (180), (181) определяют диаметры вершин зубьев.

83. Толщину обода под зубчатым венцом вычисляют по формуле

6 = (22.. .29) 10-³K77V6. (191)

Остальные конструктивные размеры гибкого колеса приведены на рис. 141.

Задача 36. Найти частоту вращения водила Н и колеса с дифференциала (см. рис. 135), если: а) г& = 20, г/г = 54, г_с — г_в, /г_& = 150 мин-*, n_k = 50 мин*-*; б) г_& = 23, Zft = 73, z_c=zz_et «6 = 280 мин-*, дг^ =75 мин~*.

Модули зубчатых колес дифференциала одинаковы.

Решение, а) Используя рис. 135 и данные условия задачи, найдем число зубьев сателлитов z_c {z_c — z_e или d_c — d_e)_% d_k = 2d_c+d_b (см. рис. 135) или mzb — 2mz_c4-mzh и

= *б)/2 = (54 - 20)/2 = 17.

1. Мысленно закрепив все колеса дифференциала на водиле, получаем

п_ь = п_н, п_с — п_е = п_х> Пк = П_М.

2. Мысленно закрепляем водило и поворачиваем центральное колесо Ь с час- тотой вращения я = —- (п_н—п_ь). Тогда частота вращения сателлитов ewe

— {п_н—п_ъ) i_{bt с} = — (п_И—п_ь) (— z_b/z_c) = (n_H—n_b) (z_b/z_c);

колеса k

— ("я— "ь) h. k = — («я—n_b) (— (+**/**) = (n_H—n_b) 2_b/Z_k.

3. Последовательно складывая частоты вращения, полученные в первом и втором движениях звеньев дифференциала, определяем: а) частоту вращения во­дила Н:

я* = («я— Ч) Ч1Ч — "я+ «я ~—п_ъг_ь1г_к,

"^я~ \ + г_ь/г_к ~ 1 + 20/54 -⁴'[так как колеса k и Ь вращаются в противоположные стороны (см. рис, 135), то при пь> 0 щ отрицательна];

б) частоту вращения сателлитов сие:

"с= "н+ (^08мин

^пн—пь) г_ь/г_с = 4,08+ (4,08—150) 20/17 «—168 мин-».

Отрицательное значение п_с подчеркивает противоположные направления вра­щения колес b и с (зубчатые колеса внешнего зацепления всегда вращаются в противоположные стороны).

Задача 37. Рассчитать двухволновую передачу, если Пх = 970 мин**¹, я₂=10 мин^-"*, Р₂ = 1,15 кВт. (См. последовательность расчета волновых передач.)

Литература: [2, 9, 10]; задача 9.18 [12].

Вопросы для самопроверки. 1. Какая передача называется планетарной? Ее преимущества, недостатки и область применения. 2. В каком случае планетарную передачу называют дифференциалом? Укажите область применения дифференци­альных механизмов. 3. Как можно вычислить передаточное отношение планетар­ной передачи? 4. Какая передача называется волновой? 5. Перечислите достоин­ства, недостатки и области применения волновой передачи.