«Занятие 19. Планетарные и волновые передачи Планетарные передачи

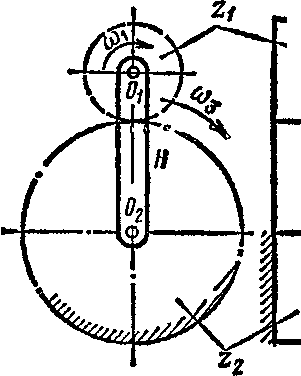
Зубчатые механизмы, в которых имеются зубчатые колеса с вра­щающимися геометрическими осями, называют планетарными. На рис. 134 показана схема простейшего планетарного механизма, состоящего из пары зубчатых колес внешнего зацепления. В этом механизме зубчатое колесо z_t может свободно вращаться на оси O_l9 закрепленной на конце подвижного звена рычага О_г0₂ (водила Я). Колесо z_t находится в сложном движении: кроме вращения вокруг собственной оси O_t оно также вращается вокруг оси 0₂, проходя­щей через геометрический центр неподвижного зубчатого колеса.

Зубчатые колеса с вращающимися геометрическими осями назы­вают сателлитами (z_i9 рис. 134) или планетарными (аналогия с дви­жением планет Солнечной системы). Колеса (г₂, рис. 134), по кото­

рым обкатываются сателлиты, называют центральными или сол-нечными. Деталь, в которой закреплены оси сателлитов, называют водилом (//).

_г

н

Е сли вращаются все три вала (1, 2, 3, рис 135), то планетарную передачу называют дифференциалом. Дифференциал имеет две сте­пени свободы (подвижно­сти) и применяется для сложения вращений (стан­ки, приборы) или для разложения вращения (ав­томобили и другие транс­портные машины).

Если закрепить (или -~zPi затормозить) вал 1 или 3 """^ (рис. 135), то получится механизм с одной степенью свободы, называемый про-стой планетарной переда­чей. Если в дифференциа­ле (рис. 136) водило Н и центральное колесо К со­единить обыкновенной зубчатой передачей, то получится замкну­тая планетарная передача с одной степенью свободы.

Планетарные передачи применяют в подъемно-транспортных ма­шинах, станках, авиамоторах, врубовых машинах, приборах, редук.

Рис. 135

торах. На рис. 137 показаны: а—планетарный редуктор с водилом, выполненным в виде эксцентрикового вала; б—планетарный редук­тор с „плавающим" центральным колесом; в— кинематическая схема планетарного редуктора, состоящего из двух пар зубчатых колес внешнего зацепления.

Планетарные передачи могут иметь один или несколько сател­литов.

Достоинства. Возможность получения большого передаточного отношения при малых габаритах и небольшой массе конструкции. Правда, у многих схем планетарных передач с большими переда­

точными отношениями КПД невысок. Например, при i_{a% ь} > > 10³ti < 12% и, следовательно, из-за самоторможения использовать такую планетарную передачу в качестве мультипликатора невозможно. Благодаря внутреннему зацеплению увеличивается нагрузочная спо­собность передачи, повышается плавность зацепления и умень­шается шум. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются, снижаются потери энергии, уменьшается нагрузка на опоры и упрощается их конструкция.

_Ш

is

Недостатки, Низкий КПД и повышенные требования к точности изготовления и монта­жа. При сборке передачи необходимо выдер­живать условия соосности (сцепляемости са­теллитов с центральными колесами), соседст­ва (возможности размещения сателлитов по окружности) и одинаковости центральных уг­лов между сателлитами.

Рис. 136

При определении передаточного отношения планетарного механизма наиболее часто при­меняют метод остановки водила Н (метод Виллиса). При указанном методе звеньям планетарной передачи мысленно сообщается дополнительное вращение с угловой скоростью, равной угловой скорости водила Я, но направленной в противо­положную сторону. В полученном таким образом приведенном меха­низме водило окажется неподвижным и планетарная передача пре­вращается в обычный зубчатый механизм, у которого все геометри­ческие оси неподвижны.

Используя метод остановки водила, определим передаточное от­ношение простейшего планетарного механизма (см. рис. 134).

Звенья механизма

Фактические угловые Угловые скорости после скорости прибавления дополни-

тельной угловой

СКОрОСТИ — (0₃

Зубчатое колесо г% Зубчатое колесо г₂ Водило Н

Щ О 0₈

(Di—0₈ О—-0)₃ = —- £0₃ <0э—Юз = 0

Итак, в механизме с мысленно остановленным водилом Н зуб­чатое колесо z_t вращается с угловой скоростью (о^—ю₃, а факти­чески неподвижное зубчатое колесо г_а в приведенном механизме вращается с угловой скоростью —(о_й9 равной по значению, но противоположной по направлению угловой скорости водила Н. Вычисляем передаточное отношение:

и тогда

^{(<»i ~ <*>з)/(— С03) = tu 2 = — ZJZil — (Di/CDg + 1 = — zjzt}

'1.* = ©1/©«=^!1+г₁/г₁.

Следовательно, передаточное отношение простейшей планетарной передачи на единицу больше передаточного отношения обыкновен­ной одноступенчатой зубчатой передачи (так как колеса г± и г_г в одну сторону не вращаются, то i_u § < 0, см. занятие 2).

Несколько подробнее рассмотрим вопрос получения большого передаточного отношения, например с помощью планетарного редук-

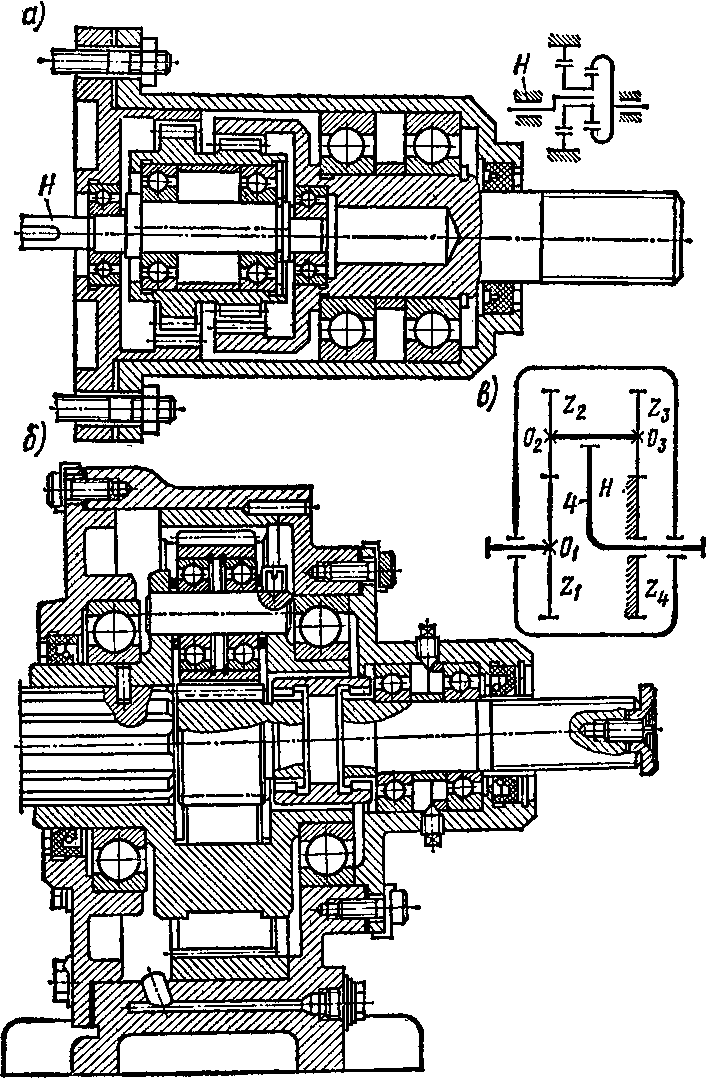
Рис. 137

тора, состоящего из двух пар зубчатых колес внешнего зацепления (рис. 137, б).

Зубчатое колесо г₄ неподвижно, а зубчатые колеса z_t и z₃ наса­жены на вал 0₂0₃, который установлен в водиле Н. При враще­нии водила Н зубчатое колесо г_а перекатывается по неподвижному зубчатому колесу z₄, совершая сложное вращательное движение. В таком же сложном вращательном движении (вокруг осей О_а и О_г) находится и второе зубчатое колесо z₂, зацепляющееся с колесом z_t и приводящее его во вращение относительно центральной оси О_г.

Применяя метод остановки водила Я, находим передаточное отношение этого планетарного редуктора.

Звенья редуктора Фактические угловые Угловые скорости

скорости после прибавления

дополнительной скорости

Зубчатые колеса:

г% cot щ—щ

Z_a (0₂ <0₂ —(0₄

eg ©a=fi>$ co₃~(D₄

z₄ 0 0—co₄

Водило H ©₄ ю₄—со₄ = 0

Таким образом, мысленно сообщая всем звеньям планетарного редуктора дополнительную угловую скорость —о>₄, получаем обык­новенный зубчатый редуктор с неподвижными осями валов. В при­веденном механизме передаточное отношение

Числитель и знаменатель левой части полученного равенства разделим на —со₄:

1/(1—со1/со₄) = г₁г₃/(г₂г₄),

или

и окончательно

(1— cojcoj/l = z₂z₄/(z^₃),

h. 4 = ©i/©4 = ¹ — ^AziZs)- (177)

С помощью редуктора, кинематическая схема которого показана на рис. 137, в, можно получить очень большое передаточное отно­шение. Так, при числе зубьев колес z_t = 100, z₂ = 99, z_a=; 100, г₄=Ю1 по формуле (177) получим

. _ 1 _<ot_ t г?*4 i 99.101 1 ^м ~~ «общ — ©4 *i*3 ~~ ¹ 100.100 ~ 10*

и

*_общ= Ю⁴!

При таком большом передаточном отношении КПД редуктора очень низкий —меньше 0,01.