Занятие 15. Примеры расчета передачи винт — гайка

Расчет передачи рекомендуется проводить в указанной последо­вательности:

1. Выполнить схематичный чертеж винтового механизма (см. рис. 97, 98).

66. Назначить профиль резьбы винтовой пары (обычно трапецеи­дальный) и задаться значениями v и

67. По известной осевой силе F_a и заданному (или выбранному) материалу винта и гайки определить [р] и вычислить требуемый размер среднего диаметра резьбы из расчета на износостойкость.

68. По таблице стандарта определить основные параметры резьбы и вычислить конструктивные размеры гайки; для прямоугольной резьбы по найденному d₂ определить параметры резьбы, пользуясь эмпирическими соотношениями.

69. Составить расчетную схему винтовой пары и построить для винта эпюры продольных сил и крутящих моментов.

70. Проверить винт на прочность.

71. Определить гибкость винта и при необходимости проверить его на устойчивость.

Задача 30. Рассчитать винтовую пару домкрата (см. рис. 97), если: a) F_a=80 кН; б) F_a — 60 кН.

Наибольшая рабочая длина винта между опорой чашки и серединой гайки:

а) / = 500 мм; б) / = 400 мм. Материал винта—сталь 45. Материал гайки: а) бронза,

б) серый чугун СЧ 21—40. Высота подъема груза hi « (8...10) d.

Определить длину рукоятки /_рук, если сила, приложенная на конце рукоятки рабочим, F_p=350 Н.

Решение, а) 1. Вычерчиваем общий вид домкрата (см, рис. 97).

2. Для винта назначаем трапецеидальную резьбу при v=0,5.

3. По формуле (138) вычисляем средний диаметр резьбы и затем определяем основные параметры передачи.

Задаемся отношением я|)^ = 1,8 (гайка неразъемная, см. с. 140). Для заданной пары материалов винт—гайка по табл, П32 принимаем [/?] = 13МПа. При этом

d^VF_a/(nv^d IP\) = К80.10³/(я0,5.1,8«13) ₌ ]/21,8-10² = 46,6 мм.

4 . По табл. П31 определяем параметры резьбы. Принимая Р = 8 мм, получаем: с/₂ = 46 мм, dj = 42 мм и d=50 мм. Определяем высоту гайки: # =

=%d₂ = 1,8-46 = 82,8 мм « 83 мм.

Число витков резьбы в гайке (см, занятие 14)

z = Н/Р = 83/8 = 10,4 мм, Чашк</ \ / у {—] $⁹*Я*?И

что примерно равно максимально до­пустимому Zmax 10.

5. Составляем расчетную схему винта и строим эпюры продольных сил и крутящих моментов (рис. 101).

При построении эпюры N_z учи­тываем, что в пределах от чашки домкрата до гайки продольная сила во всех поперечных сечениях винта равна внешней силе F_a. В пределах высоты гайки N_z меняется по линей­ному закону и падает до нуля.

От верхней кромки гайки до рукоятки крутящий момент равен моменту в резьбе Тр_у а в пределах высоты гайки изменяется по линейному закону. Выше рукоятки крутящий момент равен моменту трения на опорной поверхности чашки домкрата. Для вычисления момента в резьбе определяем угол ее подъема:

i|) = arctg P/(nd₂) = arctg 8/(я-4б) = arotg 0,0554=3° 10'.

Приведенный коэффициент трения [см. (136)] для трапецеидальной резьбы при коэффициенте трения пары сталь—бронза /=0,10 (см. табл. Ш, при бедной или периодической смазке резьбы)

/'=tg p'=//cos (a/2)=//cos (30/2)=0,10/0,966=0,104

и приведенный угол трения

р' = arot g /• = arotg 0,104=5°57\

При этом момент в резьбе

T_p=F_a^tg (i|)+^)=80.10⁼

³-⁴⁶^^Q'³tg (3°10' + 5°57')=295 Н.м.

Считая, что чашка домкрата конструктивно оформлена так, как показано на рис, 97 внизу, и принимая средний радиус опорной поверхности чашки /?_ср=30 мм, находим момент торцового трения при коэффициенте трения /=0,!б (см, табл. YU, для стали по стали или по чугуну):

Г_/ = /Р_Л/?_ср = 0,15.80»10³.30.10-³ = 360 И-м.

6. Для опасного сечения винта (одно из сечений между гайкой и рукояткой) N_z = F_a = 80*MF Н, 7 = 7^ = 295 Н«м. Вычисляем эквивалентное напряжение:

где

Следовательно,

<*экв = Ко²+Зт? = К60,3²+3«20,2? = V (36,4+12,2) 102 = 69,7 МПа. Для стали 45 закаленной а_х=600МПа, тогда коэффициент запаса прочности п = о_т/о_экв = 600/69,7=8,63,

что значительно больше [п] « 2.

7. Определяем гибкость винта и проверяем его на устойчивость. Винт рас- сматриваем как стойку с нижним жестко закрепленным и верхним свободным концом, т. е. коэффициент приведения длины ц = 2.

Момент инерции поперечного сечения винта по расчетному диаметру резьбы

Лп1п= я4/64 = я (42-10~³)⁴/64 = 15,3-10~⁸ м⁴. Радиус инерции поперечного (расчетного)'речения винта

^{Уж' /¥П== УШ^?= КТШо^=10,5.,о-. м.}

Гибкость винта [см. (142)]

^ = ^Л'т1п = 2.0,5/(10,5-10-³) = 95,3,

что больше Х_пред = 85 (для стали 45). Следовательно, критическую силу следует определять по формуле Эйлера при £=2,Ы0^иПа (см. табл. П2):

_n*EJ_min я-^ЫО¹*.15,3.10-* _{Qiq 1ЛЗН} ^F«* = W =313-103 Н.

Определяем коэффициент запаса устойчивости винта по (141):

Яу = Fkv/F<i = 313-10³/(80.10³) = 3,92 ^ [л_у] = 2,5 ... 4.

8. Вычисляем параметры гайки (см. рис. 97). Наружный диаметр гайки най- дем по формуле (139) при d = 50 мм и [о_р]==39 МПа для бронзы:

= 7,58-Ю-² м,

принимаем D = 76 мм.

Диаметр буртика гайки вычислим по формуле (140) при [а_см]=48МПа:

= У (21,2+ 58) 10~⁴ = 8,89-10~² м,

принимаем Dj = 90 мм. Высота буртика гайки

а=Я/3,5=83/3,5 = 23,7 мм, принимаем а=24 мм.

9. Определяем, длину рукоятки из условия, что момент, приложенный к ру­коятке, равен сумме моментов в резьбе и на опорной поверхности чашки:

Гру_К =Тр + Tf = (295 + 360) =655 Н м. Момент Грук создается силой F$ рабочего, приложенной к концу рукоятки: Грук^р'рук» откуда

/_рук = Грук/^р = 655/350 =1,9 м.

Такая длина рукоятки непомерно велика, поэтому надо ориентироваться на двух рабочих и тогда /_рук=0,95 м.

Задача 31. Спроектировать струбцину (рис. 102) для сжатия деталей силой: а) /^ = 20 кН; б) ^_Л = 15кН.

При проектировании струбцины предусмотреть расстояние между челюстями: а) Л = 250 мм, б) Л = 300 мм; вылет челюстей: а) /=180 мм, б) /=150 мм.

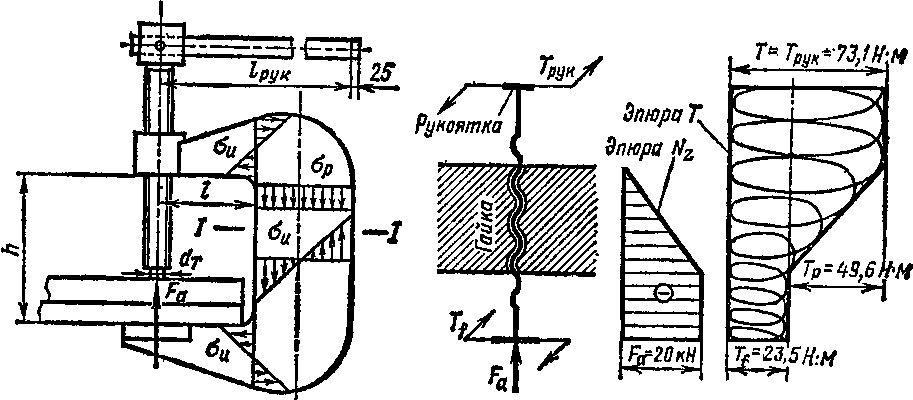
Рис. 1Q2 Рис. 103

Решение, а) 1. Выполняем примерный (без уточнения конструктивных разме­ров) чертеж струбцины (рис. 102).

2. Для винтовой пары назначаем трапецеидальную резьбу.

3. Выбираем материал для изготовления деталей струбцины. Для изготовле- ния винта струбцины принимаем сталь 45 закаленную. Скобу струбцины изго- товляем из полосовой стали или из стального листа.

Из расчета на износостойкость [см. (138)] определяем средний диаметр резь­бы, задаваясь отношением i|?^ = 2 и принимая по табл. П32 [р]=8«10° Па:

d₂^ V FJ(™% [р]) = V20- 10»/(л;-0,5.2.8. ю«) = V7,96-10~* = = 2,82-10-2 м = 28,2 мм.

4. По табл. П31 находим параметры резьбы при cf_a^28,2 мм:

с? = 32мм, Р = 6мм, с?₂ = 29 мм, с?₃ = 25 мм, <^ = 26 мм.

5. Определяем высоту гайки:

# = ^d_a = 2.29=58 мм, с небольшим округлением принимаем Я=60 мм. При этом число витков в гайке

з=#/Р=60/6 = 10, что равно предельно допустимому s_majt = 10.

6. По формуле (139) находим наружный диаметр гайки при (/=32 мм и [а_р]=22 МПа для чугуна:

^U^ V я[а_р]^+а V п-22Л№^^{Кбг Ш} ' = 1^(14,5+10,24)-* = 4,97.Ю~² м,

принимаем D = 50 мм.

7. Составляем расчетную схему винта и строим эпюры продольных сил и крутящих моментов (рис. 103).

Определяем момент сил трения на опорном торце винта, диаметр которого d_t^di = 26 мм, принимаем d_T — 22 мм (см. рис. 102); дальнейший расчет ведут по так называемому приведенному радиусу трения (см. занятие 26) R_np=d_t/3:

77 = fF_e#_np=0,16.20.10³.22-10-⁸/3 = 23,5 Н-м,

где / = 0,16—коэффициент трения скольжения стали по стали или по чугуну всухую (см. табл. П1).

Для определения момента в резьбе найдем угол подъема [см. (133)] резьбы при /1 = 1

ip = arctg [nP/(nd₂)] =arctg [b6/(n.29)]=arctg0,066 = 3^o47\

Принимая коэффициент трения стали по антифрикционному чугуну при бед­ной или периодической смазке резьбы /' = 0,1 (см. табл. Ш), по формуле (136) вычисляем приведенный угол трения:

p'=arctg/' = arctg [//cos (a/2)J=arotg [0,1/cos (30°/2)] = arctg0,1035 = 5°55\

Момент в резьбе

T_v=F_a (0Й) tg (ф+р') =20-Ю³.(0,5.29.10-5) tg (3°47'+5°55') =49,6 Н-м.

8. Эквивалентные напряжения вычисляем для сечений выше и ниже гайки, так как из эпюр (рис. 103) неясно, какое из этих сечений опасно. Ведя расчет для торцовой части винта диаметром а*_х = 22мм, получаем для сечения ниже гайки:

а = N_Z/S_T = 4/у(я4) = 4-20.10³/[я (22-10~³)?]=52,4- 10^е Па = 52,4 МПа; T = 7^,/W^rp= ШГ/Ся^) = 16-23,5.10³/[я (22-10~³)³] = 12,7- 10^е Па = 12,7 МПа; о_экв= ]Ла? + Зт? = V 52,4?+3-12,75= \ (27,5+4,85) 10§ = 56,8 ДШа. Для сечения выше гайки при а=0

% = T/W_V= 16 (7^,р+Г_/)/Ы?) = 16(49,6 + 23,5)/[я (26« 10~³)³] =23,7- 10^е Па;

о*экв= V<7?+3t?= |^0+3(23,7.10^е)? = 41,Ь 10° МПа = 41,1 МПа.

Таким образом, опасное сечение расположено ниже гайки, для которого коэф­фициент запаса прочности при а_т=600МПа

л=а_т/а_экв = 600/56,8= 10,55,

что значительно больше [п] « 2.

9. Определяем гибкость винта и проверяем его устойчивость. Рассматривая винт как стойку с одним (верхним) жестко защемленным концом

(в гайке) и другим (нижним) свободным концом на поверхности детали, прини­маем коэффициент приведения длины [i=2_#

По формуле (142) вычисляем гибкость винта:

^—^L=,=, _i И* ^М _{= 4}.2.250/26 = 77,

Вычисляем критическую силу для винта. Для стали 45 Я,_пРед«85, следовательно, к < ^ред ^и критическую силу определяем по формуле Тетмайера—Ясинского при

а=589 МПа, 6 = 3,82 МПа (см. с. 141) и Si = jr4/4 = Ji (26-10"³)²/4 = 53-10-S м?: /⁷кр==(л—М.) Si = (589—3,82.77) 10*. 53-10-* = (589—294) 530=156.10³ Н.

Коэффициент запаса устойчивости винта

"у = F_KV/F; = 156-10³/(20-10³) = 7,8 > [п_у] = 2,5.. .4.

10. Определяем конструктивные размеры скобы струбцины (рис. 104). Размеры поперечного сечения (axb) скобы ориентировочно принимаем по следующим соот­ношениям:

attdi и Ь « (4 ... 5)а₉

При di=26 мм получаем

a«rfi=26MM, 6«(4...5)а = (4.. .5)26= 104 ,

130 мм.

П ринимаем а=26 мм, 6=115 мм. Выбираем для скобы листовую сталь СтЗ, для которой а_т = 225МПа (см. табл. ПЗ) и [п] =2,5—повышенный коэффициент запаса (принят для обеспечения достаточной жест­кости скобы); тогда

[о] = [с_р] = [c_HJ = c_T/[nJ =225/2,5=90 МПа.

Проверяем прочность скобы в сечении /—/, в котором возникают продольная сила и изгибаю­щий момент:

^сум = ^(Тр+^и; o_v=N₂/S = F_a/(ab) =

= 20 • 10³/(26 • 115 • 10-^в)=6,7 • 10^е Па = 6,7 МПа. Плечо изгибающей силы

L = /+0,56 = 180+0,5-115=237,5 мм и изгибающий момент

М_л = F_aL = 20• Ю³.237,5• Ю-⁸ = 4750 Н .м, тогда

а_и = Л1_и/^ = 6Л1_и/И)5 =

=64750/[26.l0-³(115.10"³)?]=83.10^е Па=83МПа. Следовательно,

а_Су_м = а_р+а_и = 6,7+ 83 = 89,7 МПа < [а].

Определяем размер Ь% скобы в сечении //-—//, в котором возникает изгибаю­щий момент

М_л=F_ai=20• 10³ • 180• 10-» = 3600 Н • м. Из уравнения прочности jl

а_и = MJW_X = 64Mj(abi) < [а_й]

получаем

bt^z V6MJ(a [о_и)] = /6.3600/(26. Ю-³-90-10^б) = V 92,4-10-4 = 9,6-10-2 м,

принимаем Ь% = 100 мм.

По размерам Л = 250 мм, # = 60 мм, 6 = 115 мм₅ 6х=100мм, /=180 мм тон­кими линиями вычерчиваем прямоугольный контур скобы, а также винт и гайку. От точки С₂ отложим отрезок 0С₂ = & и радиусом 6=115 мм из центра О опи­шем дугу С₂С_г. Через точки О и Cj проводим наклонную прямую ОС± до встречи с контурной линией гайки. Радиусом R выполняем закругления верхнего и ниж­него наружных углов скобы.

Занятие 16. ЧЕРВЯЧНАЯ ПЕРЕДАЧА

Классификация, достоинства, недостатки, область применения

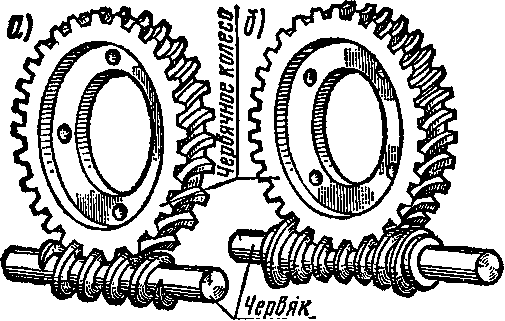
Ч ервячная (или зубчато-винтовая) передача (рис. 105) представ­ляет собой кинематическую пару, состоящую из червяка и червяч­ного колеса. Йа рис. 106 показан привод от электродвигателя 3, соединенного муфтой 2 с ведущим валом червячного редуктора /. Червячную передачу можно рассматривать как модификацию

винтовой пары (рис. 107), длинная гайка которой раз­резается продольной плоско­стью (параллельной оси вин­та) и изгибается в круговое кольцо — зубчатое колесо, охватывающее тело винта — червяка по дуге.

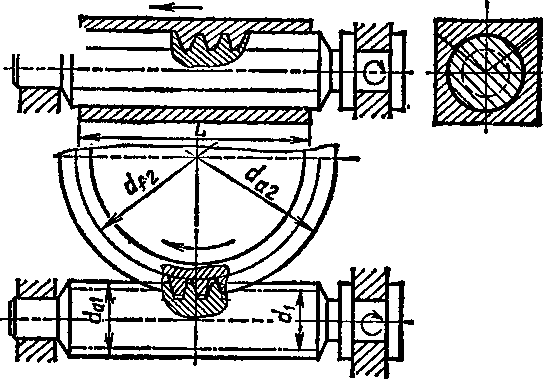
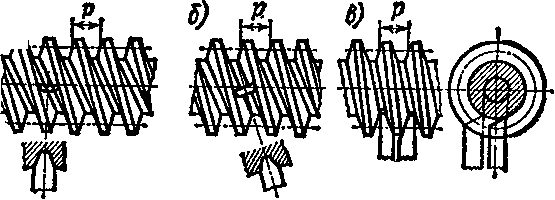
Червяк —это винт с резь­бой, нарезанной на цилинд­ре (архимедов, конволют-ный, эвольвентный и дру­гие червяки, см. рис. 105, а) или на глобоиде (см. рис. 105, б). Архимедов червяк (рис. 108, а) представляет собой цилиндрический винт с трапецеидальным про­филем резьбы. В торцовом сечении витки этого червяка очерчены

Рис. 106

архимедовой спиралью. Конволютный червяк (рис. 108, б) —это цилиндрический винт с прямолинейными очертаниями профиля впа­дин или витков в сечении, нормальном к боковой поверхности резьбы. Эвольвентный червяк (рис. 108, в) можно рассматривать как косозубое цилиндрическое колесо с очень большим углом наклона зуба к образующей цилиндра и g малым числом зубьев. Профиль витков — зубьев очерчен эвольвентой. Глобоидный червяк (см. рис. 105, б и 109) представляет собой винт, нарезанный на поверхности тора (глобоида). В центральной осевой плоскости червяка витки имеют прямолинейный профиль. Передачу с таким червяком называют глобоидной. Несмотря на то, что при одинаковых габаритах нагру­зочная способность передачи с глобоидным червяком значительно выше, чем с цилиндрическим, она пока не получила широкого рас­пространения из-за комплекса причин, связанных с теплоотвоДом, изготовлением и сборкой глобоидного червяка и червячного колеса.

Б лагодаря относительной простоте технологии изготовления чер- вяка и колеса (зубья червячного колеса нарезают червячной фрезой или, реже, вращающимися резцами-летучками; резьба червяка нарезается резцом J£2HI на токарном станке или дисковой фрезой на спе- циальном червячно-фре- зерном станке) передачи с цилиндрическим архиме- довым червяком находят широкое применение в различных отраслях ма- шиностроения и народно- го хозяйства. Наряду с этим в последнее время получают все более широ- кое применение и эволь- вентные червяки. .

Достоинства. Возмож- ^ ность осуществления пе­редачи (одноступенчатой)j с большими передаточными числами: в кинематичес­ких передачах « = 500 и более, а в силовых пере­дачах и = 8 ... 80, в виде исключения до 120.

Плавность зацепления и бесшумность работы.

Возможность осуществления самотормозящей передачи (у такой передачи КПД меньше 50%).

Небольшая масса передачи на единицу мощности при большом передаточном числе.

Недостатки. 1. Сравнительно низкий КПД в несамотормозящих передачах tj = 0,7 ... 0,92 (большие значения tj для передач с мно-говитковым и шлифованным червяком). 2. Ограниченность переда­ваемой мощности —не выше 50... 100 кВт. 3. Сильный нагрев пе­редачи при длительной непрерывной работе. 4. Высокая стоимость материала венцов червячных колес (бронза) и инструмента для наре­зания зубьев червячных колес (червячные фрезы), а также шли­фовки червяка.

Несмотря на указанные недостатки, червячные передачи полу­чили большое распространение в машиностроении и приборостроении благодаря возможности редуцирования угловой скорости в широком

д иапазоне при скрещивающихся осях валов: механизмы привода троллейбуса, подъемно-транспортных машин, пассажирских и грузо­вых лифтов, станков, различных приборов и т. д.

Геометрические соотношения в червячной передаче с цилиндрическим архимедовым червяком. Передаточное число

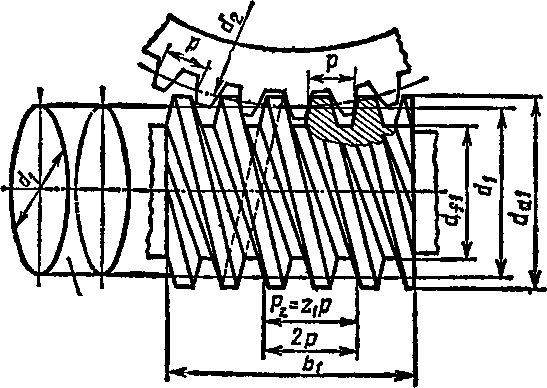
Р асстояние р₉ измеренное между одноименными точками двух соседних витков профиля резьбы червяка (рис. ПО, 111), называется

шагом червяка и червяч­ного колеса. Отношение шага р к я называют жо-дулем:

Цилиндр, на образу­ющей которого толщина витка и ширина впадины резьбы червяка одинако­вы, называют делительным (рис. 110), его диаметр обозначают dt.

Червяк, как и винт, может иметь одновитко-вую (однозаходную) или многовитковую (многозаходную) резьбу; число витков резьбы червяка обозначают г_ь В силовых червячных передачах применяют червяки с z*= 1, 2, 4.

ISO

Ход витка червяка равен произведению шага на число витков:

Рг_х = рг_г. (145)

Делительный диаметр червяка принято выражать через модуль:

di=mq< (146)

Параметр q, определяющий число модулей в делительном диа­метре червяка, называют коэффициентом диаметра червяка. Значе­ния т и q стандартизованы (см. табл. ПЗЗ).

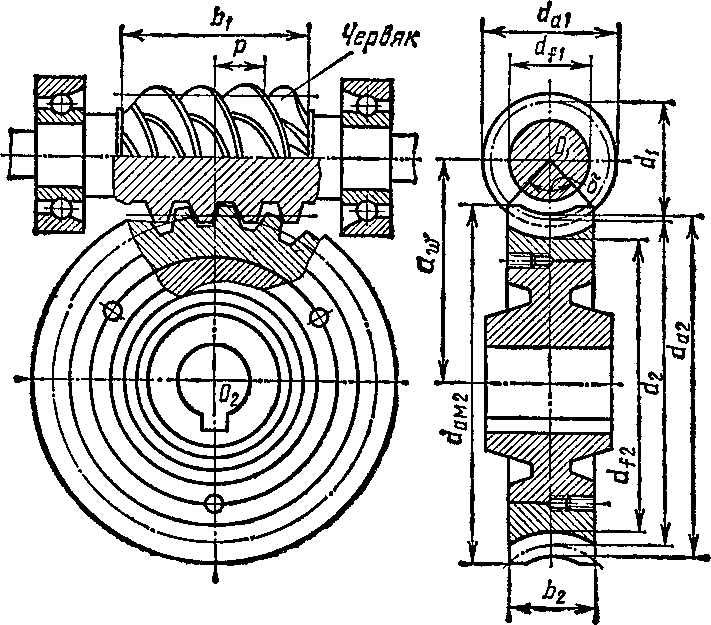
Рис. ш

Тангенс угла подъема линии витка (резьбы червяка) определяют на делительном цилиндре червяка:

tg Y = PzJ{nd_x) = pzj(nmq) = mz_xJ{mq)_f

откуда

tgY = *i/tf. (147)

Таким образом, с увеличением коэффициента диаметра червяка уменьшается угол подъема его резьбы, что, как известно из теории передачи винт —гайка, приводит к снижению КПД механизма.

Если принять высоту делительной головки зуба червячного колеса /г_а2 = т, а высоту делительной ножки зуба ft_/2=l,2m (радиальный зазор с=0,2/я), то диаметры вершин витков и впадин червяка (рис. ПО):

dai - (k + 2h_a2 = d_t + 2m; (148)

a_fl —2ft_/2==rfi-2,4m. (149)

Делительный диаметр червячного колеса d₂ в среднем сечении (рис. 111) при числе зубьев г_г

d₂ = mz₂. (150)

Диаметры вершин зубьев й впадин червячного колеса в среднем сечении (рис. 111):

rfa2 = d₂ + 2A_fll = rf₂ + 2/w; (151)

d_f% = d₂ —2ft_/2 = tf₈ —2,4/ю, (152)

Межосевое расстояние

a_w = 0,5 (d_x + d₂) = 0,5m (g + z₂)< (153)

Часто используют корригирование червячных передач, которое выполняют в основном в целях вписывания межосевого расстояния в стандартный ряд чисел. Корригирование изменяет только три расчетных параметра:

d_wl = m(q+2x); (146а)

d_a* = d₂+2 (l+*)m; (151а)

d_/2 = d₂ —2 (1,2 + х) т, (152а)

где коэффициент смещения инструмента x = (a_w/m)—0₎S(q+z₂) выбирают в пре­делах ±1.

Окружную скорость точки делительной окружности червячного колеса можно определить как скорость поступательного перемеще­ния гайки по винту:

v₂ = P₂nJ60 =/^/^/60,

Эту же скорость можно найти обычным способом как скорость точки вращающегося тела:

v₂ = nd₂n₂/60 = рг₂п₂/60.

Приравнивая правые части двух выражений для одной и той же скорости, получаем

Z₂fl₂*

Отсюда, учитывая формулы (86), (16), получаем передаточное число:

и = z₂lz_t = щ/щ = njn₂ = i. (154)