Силовые соотношения и кпд винтовой пары

Рассмотрим винтовую пару с прямоугольной резьбой (рис. 96): Р_а—осевая сила в винтовой паре; F_t = 2Tld₂ — окружная сила на окружности среднего диаметра d₂ резьбы винта (болта); Fj^fN —

с' Ь	}

с ила трения в резьбе винто­вой пары.

Подъем гайки по витку винта можно рассматривать как подъем груза по наклон­ной плоскости АВ, являю­щейся разверткой винтовой линии и образующей с ка­тетом AC = nd₂ угол ф; вы­сота наклонной плЬскости равна катету BC = P_hnP, соответствующему ходу резь­бы.

Применяя уравнения рав­новесия для плоской систе-

мы сходящихся сил, получаем:

2 х = F_t со s i|> — F_f — F_a s i n = 0;

F_f fN = F_t cos —F_a sin tj). 2# = N — F_t sin t]) — F_ecos ф = 0; N = F_f sin tj) + F_a cos tj).

Следовательно,

f (F_t sin tj) + F_a cos tj)) = F_t cos tj) — F_a sin tj); F_e (sin tj) + / cos 1|)) = F_t (cos tj)—/ sin ty); _{f F} sin»+/cosH) _f tg»+/ - tg»+tgp - t^rtb-LoV ^J* ^ff cos i|)—/sini|j «I — / tg *1—tgptgi|)~" * ^K^ Ft = Fate(<P + P)> (134)

где /^tgp —коэффициент трения в резьбе; р — угол трения; р« «2...6° для стального винта и бронзовой гайки, р^4...8° для стального винта и чугунной гайки. Для однозаходных резьб «2...7°, меньшие значения для крепежных резьб. Для многоза-ходных резьб t|) » 8... 16°.

Коэффициент полезного действия винтовой пары g прямоугольной резьбой

FaBC

I — ¹

^п°л

ВС _ tg ф

Лзатр F_tAC — F_a tg (ф+р) AC tg p) •

Если профильный угол резьбы а отличен от 0, то вместо р при­нимают приведенный угол трения р'. Следовательно,

₄=:tgt|5/tg(t|5 + p')_f (135)

причем

tgp'=//cos(a/2), (136)

где а —угол профиля резьбы; а = 60° для треугольной метрической резьбы (см. рис. 95, а) и а = 30° для трапецеидальной резьбы (см. рис. 95, б).

Например, при a =-60° получим

t

_ f _

f

f

cos (a/2) cos (60°/2) 0,866

gp'

= 1,155/ и p'=arctg 1,155/>p,

т. е. КПД треугольной резьбы меньше, чем прямоугольной.

Если ty<p', то винтовая пара обладает свойством самотормо­жения, при котором груз, поднятый винтом, например домкратом, самопроизвольно опуститься не может. При самоторможении _а<50%.

Все крепежные резьбы обладают свойством самоторможения, причем для резьб с мелкими шагами «запас» самоторможения больше, так как углы подъема у них меньше, чем у резьб с крупным шагом.

Достоинства, недостатки, область применения. Материалы и конструкция деталей передачи

Передача винт —гайка предназначена для преобразования вра­щательного движения в поступательное и в редких случаях для преобразования поступательного движения во вращательное. Второе возможно только при нёсамотормозящей винтовой паре.

8* 0,25 d h^Zdp

Н

д..л

Достоинства. 1. Простота изготовления и надежность конструк­ции. 2. Большая несущая способность при небольших габаритах передачи. 3. Большой выигрыш в силе, получающийся вследствие медленного осевого перемещения винта (гайки): скорость скольже­ния в резьбе больше скорости осевого перемещения винта в 1/sin раз,

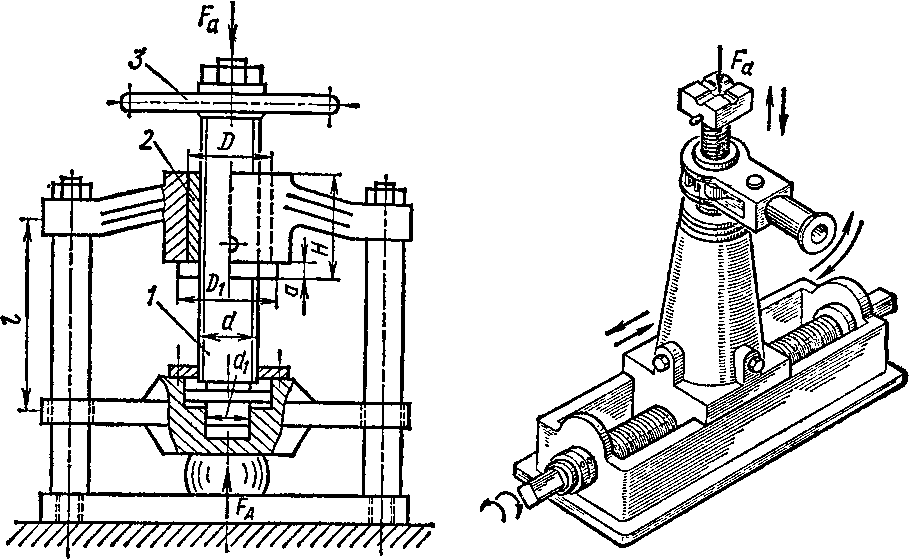
Рис. 98 Рис. 99

обычно в 5.. .40 раз. 4. Возможность обеспечения высокой точности перемещений.

Недостатки. 1. Низкий КПД: п= 0,6.. .0,85; для самотормо­зящих винтовых пар х\ < 0,5. Следует учесть, что КПД винтовых механизмов (домкраты, прессы и т. д.) меньше КПД винтовой пары, так как помимо потерь на трение в резьбе возникают дополни­тельные потери на трение в опорных частях механизма, например в головке домкрата (рис. 97) или на опорном торце винтового пресса (рис. 98). 2. Тихоходность передачи.

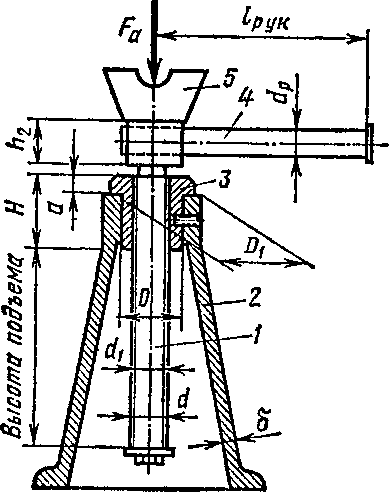
Передачу винт —гайка применяют при поднятии грузов (винто­вые домкраты, рис. 97, 99), в машинах для испытания материалов, при механической обработке материалов (ходовые винты станков, винтовые прессы, тиски, струбцины, нажимные устройства), при необходимости выполнения точных перемещений (измерительные приборы) и т. д.

В передаче винт—гайка материал винтов и гаек должен обла­дать высокими антифрикционными свойствами и износостойкостью. Винты изготовляют из сталей 45; 50; А45; А50; У10; 65Г; 40Х; 40ХГ; 40ХВГ или Ст4; Ст5. Гайки изготовляют цельными и разъ­емными (с разъемом по осевому сечению) из оловянной бронзы: Бр. ОФ10-1, Бр. ОЦС6-6-3; при малых скоростях и нагрузках — из антифрикционного чугуна марки АВЧ-1; АСЧ-3 и др.

Для повышения КПД передач винт—гайка применяют резьбы с малым углом профиля—трапецеидальную, упорную и прямо­угольную. Наибольшее распространение

имеет трапецеидальная резьба со средним шагом. Трапецеидальную резьбу с мелким шагом используют при относительно не­больших перемещениях, а с крупным ша­гом—при тяжелых условиях эксплуатации. Прямоугольная резьба не стандартизована и применяется сравнительно редко, ее не­льзя фрезеровать, а нарезание на токарном станке менее производительно, чем фрезеро­вание. Для передач с большими односторон­ними нагрузками (прессы, домкраты, на­жимные устройства прокатных станов и др.) применяют упорную резьбу.

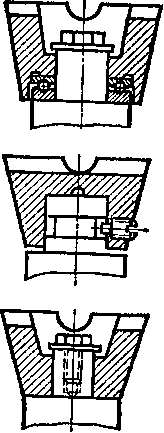
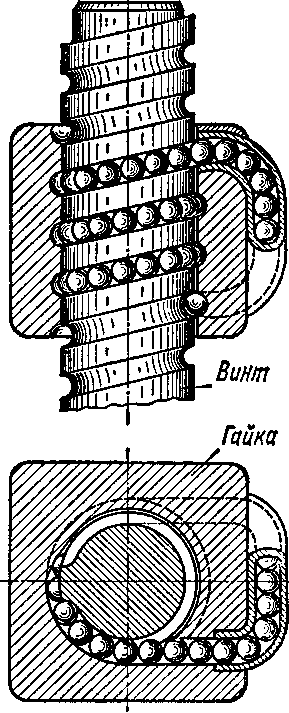
Конструктивное оформление передачи винт —гайка зависит от ее целевого назна­чения. В винтовом домкрате (см. рис, 97): !/—винт, 2 —корпус, 3 —гайка, 4 —рукоят­ка, 5 —чашка (различные варианты конст­руктивного оформления чашек показаны на рисунке справа). В винтовом прессе (см. рис. 98): / — винт, 2 —гайка, 3—штурвал. Если трение скольжения заменить трени­ем качения, т. е. применить шариковинто-вую пару (рис. 100), то КПД передачи винт —гайка можно повысить примерно до

0,9. Рис. юо

Расчет передачи на износостойкость и проверка винта на прочность и устойчивость Выбор основных параметров и расчетных коэффициентов

В передаче винт —гайка резьбу рассчитывают на смятие и срез, а винт —на сжатие (растяжение) и кручение (иногда дополнительно на изгиб). Практика расчетов и эксплуатации передачи винт —гайка показала, что выполнение условия прочности ог_8КВ^[а] не обеспе­чивает долговечности винтовой пары и устойчивости сжатого длин­ного винта. Для резьбы передачи опасны не смятие и срез, а износ, который «происходит тем интенсивнее, чем выше давление между витками резьбы винта и гайки. Кроме того, для длинных сжатых винтов опасна потеря устойчивости —возникновение продольного изгиба.

Как показывают сравнительные расчеты винтовых пар, решаю- щим фактором является износостойкость резьбы. По этому условию, ограничивая давление в резьбе, выполняют проектировочный

расчет винтовой пары. Проверку винта проводят на прочность и устойчивость.

Для обеспечения износостойкости резьбы необходимо, чтобы давление в резьбе не превышало допускаемого значения, опреде­ляемого в основном свойствами материалов винта и гайки:

р = /^(^₂ад<[/>]. (137)

Здесь /^ — осевая нагрузка, действующая на винт; nd₂H_t — площадь поверхности контакта одного витка резьбы (площадь кольца), выраженная через средний диаметр резьбы d₂ и высоту рабочего профиля Hi = vP (см. рис. 95), где v — коэффициент рабочей высоты профиля резьбы: v = 0,5 для трапецеидальной резьбы по ГОСТ 9484—73, v = 0,75 для упорной резьбы по ГОСТ 10177—62, v = 0,541 для треугольной резьбы по СТ СЭВ 180—75; Р —шаг резьбы (см. табл. ПЗО, П31); [р]—допускаемое давление (см. табл. П32), z — число витков резьбы в гайке высотой Н: z = HIP < 10.

Принимая #/d₂ = ita и учитывая, что

Н_хг = vPH/P = vH = v^d₂, получаем при замене в уравнении (137) //^г = vi^d*

FJ(nd₂v%d₂)^[p]₉

откуда

d₂^VF_al(n^_d\p\). (138)

Для целых (неразъемных) гаек принимают ty_d =IJ/d₂~ 1,2.. .2,5; для разъемных и сдвоенных гаек -ф^ = ///d₂ = 2,5.. .3,5. Большие значения ф₄ рекомендуется принимать для резьб с d^. 10... 14 мм.

После определения d₂ и H = ^_dd₂ необходимо, выбрав шаг резьбы, проверить число витков резьбы в гайке; если г> 10, то следует увеличить параметры резьбы (d₂ и др.)

Если рассчитывают винт с трапецеидальной резьбой, то найден­ное по формуле (138) значение среднего диаметра резьбы d₂ необ­ходимо согласовать с табл. П31. По этой же таблице принимают и остальные параметры резьбы d, di и Р. Если рассчитывают винт с прямоугольной резьбой, то обычно принимают P = d₂/4 и, исходя из этого соотношения, определяют d_x и d:

di=8d₂/9\ d = 5d₁/4.

Наружный диаметр гайки D (см. рис. 97, 98) можно найти из условия прочности на растяжение и кручение (при Л_зат« t,25, см. занятие 27), а диаметр буртика гайки О_г — из условия (урав­нения) прочности на смятие:

из

^аэкв = *зат^/5р<.[а_р] при S₉ = (n/4)(D*-d*)₉

получаем

D>V5Fj(n[o_v]) + d*; (139)

из

*cm = Q/S_cm<K_m] при S_CM = (n/4)(DJ-D2),

получаем

D_t > V4F_a/(*[Oc«]) + Dl (140)

Допускаемые напряжения: [а_см] = 42.. .55 МПа для бронзы и чугуна, [ог_р] = 34.. .44 МПа для бронзы, [а_р] = 20.. .24 МПа для чугуна.

Для проверки винта на прочность строят эпюры продольных сил и крутящих моментов; по ним находят опасное сечение винта, для которого и ведут проверку.

При применении гипотезы наибольших касательных напряжений условие прочности имеет вид

где а—напряжение сжатия (или растяжения) винта; т—наибольшее напряжение кручения.

Как правило, винт, параметры которого определены из условия износостойкости, имеет достаточную прочность.

Сравнительно длинный и тонкий винт должен быть дополнительно проверен на устойчивость; эта проверка выполняется по уравнению

fly=F_Kp/F_fl>[rc_y], (141)

где я_у — расчетный коэффициент запаса устойчивости винта; /⁷_кр = = n²EJ_min/(\il)² — критическая сила (формула Эйлера); /^—осевая сила, сжимающая винт; [я_у] — допускаемый (требуемый) коэффициент запаса устойчивости; для вертикальных винтов [Лу] = 2,5 ... 4, для горизонтальных винтов [/г_у] = 3,5 ... 5; £ — модуль продольной упру­гости материала винта; /_mi„ = ш#/64 — наименьший осевой момент инерции расчетного сечения винта; d_£ —внутренний диаметр резьбы винта; ^—коэффициент приведения длины винта;* для винта домк­рата [г = 2 (стойка с нижним жестко защемленным и верхним сво­бодным концом); / — длина сжимаемой части винта.

Критическая сила F_KV определяется по формуле Эйлера, если гибкость винта

Ь = VtiLin = VUV*m\jSt > Чгред, (142)

где ^_пред» 85 для стали 45; 50; А45; А50; 40Х; 40ХГ; Ст5.

Если ХГ< А,_дред « 85, то критическая сила определяется по фор­муле Ясинского —Тетмайера:

F^ia-VtySi. (143)

Для стали 45 (приближенно можно применять и для указанных выше марок стали) а «589 МПа, 3,82 МПа. Si = jidf/4 — расчет­ная площадь поперечного сечения резьбы винта.

При к < К₀ = 55 винт из стали указанных выше марок на устой­чивость можно не проверять.

Кинематический расчет. При работе передачи винт—гайка вра­щательное движение может иметь любое звено этой передачи, т. е. как винт, так и гайка. Если вращается винт (гайка неподвижна), то любая его точка кроме вращательного движения (вокруг оси винта) имеет еще и поступательное движение вдоль оси винта. Окружная скорость точки винта, лежащей на окружности среднего диаметра резьбы,

^vi = <°i • (1 /2) d₂=nd₂nj6Q₉

а линейная скорость этой же точки, движущейся поступательно вдоль оси винта,

где / — время одного оборота винта.

За один оборот винта точка, лежащая на окружности, пройдет путь: по окружности среднего диаметра резьбы nd₂ = v₁t₉ вдоль оси винта P_h — nP = v₂t. Таким образом, отношение этих скоростей (см. рис. 96)

vJv_%^ndJP_h=\Iig^. (144)

Задача 29. Определить угол подъема резьбы и вычислить линейные скорости точки, лежащей на окружности среднего диаметра трапецеидальной резьбы пере­дачи винт—гайка, если: a) nj=200 мин"¹, б!=40мм, я=2; б) ni=250 мин~^Л, d = 32 мм, /z = 3.

Решение, а) 1. По табл. П31 при с/ = 40 мм принимаем шаг резьбы Р = б мм, тогда средний диаметр резьбы е?₂ = 37мм.

2. По формуле (133) определяем тангенс угла и угол подъема резьбы (винто- вой линии), а по формуле (144) вычисляем отношение окружной скорости и ско- рости поступательного перемещения винта:

tg9=P_ft/(jw/₂) = nP/(jw/₂)=2.6/(n.37) = 0,103 и i|)=5°53': i/i/fl₂=l/tg ф= 1/0,103=9,73.

3. Вычисляем линейные скорости точки:

а) окружная скорость

vi=я^/бО=я»37.10~⁹«200/60=0,387 м/с;

б) линейная скорость точки при поступательном движении винта

i>2=t/itg<t|)=0,387.0,103 = 0,0398 м/с.