64. Н

    Колесо 'зубчатое

    Сталь wx гост 4543-71

    В220... 240

65. Острые кромки на торцах зубьев притупить фаской fx45° J. Неуказанные предельные отклонения размеров: ._г/.

wen

отверстий-по Н1Ч_Л балов-по л/4, остальных-Pot*jr-

4. Колесо обкатать с сопряженным колесам и сдать комплектна

5ирискам

тштр

5. Маркировать номер детали б.*Размер для справок

XX. 66.238

масса yumfal

1,3 ut

забой

Лист Г Листай Краснодарский станкпвтаеитаяьнш

воина

dfel=*^del—²>^4mte ^{cos =} 66 — 2,4*3*0,956 = 59,12 мм; d_e2 = mt_ez₂ = 3*72 = 216 мм; d_ae-2 = d_e2 + 2m_te cos 6_a = 216+ 2-3 cos 73° = 216+6.0,292 = 217,75 мм; d_fe2 = d_e2—2Am_ie cos 6₂ = 216 — 2,4.3.0,292 = 213,9 мм.

3. Внешнее конусное расстояние найдем по формуле (116):

R_e -0,5/72^2! yV+l = 0,5 • 3.22 }Лз,27?+1 = 33 уТГП? = 133 мм.

4. По формулам (115) и (114) определяем средний окружной модуль и сред- ний делительный диаметр шестерни:

Щ_т = т_и(1—0№ье)=Ще 0 —0,56//?_е) = 3 (1 —0,5X45/133) = = 3(1—0,169) =2,493 мм; d_m 1 = Щт%i = 2,493*22 = 54,8 мм.

5. Вычисляем скорость точки на среднем делительном диаметре:

v_m = nd_mln J60 = я. 54,8 • 10 - ³ • 980/60 = 2,82 м/с.

6. Вычисляем окружную силу, действующую по касательной к среднему де- лительному диаметру:

Ft = ^pilv_m = 7,27 • 10³/2,82 = 2,58 • 10³ Н.

7. По формуле (122) находим осевую силу на шестерне и радиальную — на ко- лесе:

F_el = F,._a = F₁tgasine₁ = 2_f58.10³ tg 20°sin 17° = 2,58-10³-0,364-0,292 = 274 H.

8. По формуле (123) вычисляем радиальную силу на шестерне и осевую — на колесе:

F_r\ = F_a2 = Р* tg a cos б_х = 2,58.10³.0,364-0,956 = 897 H,

Занятие 13. Методика расчета прямозубых конических передач

Расчет прямозубых конических передач выполняют в той же последовательности, что и расчет прямозубых цилиндрических пе­редач (см. занятие 9 и последовательность решения задач 27, 28).

При выполнении расчета прямозубой конической передачи ис­пользуют соответствующие формулы (124).. .(127) и др., принимая значения основных параметров и расчетных коэффициентов по ре­комендациям занятия 12.

Особенности расчета открытых передач см. в занятии 8.

Задача 27. Рассчитать открытую нереверсивную коническую прямозубую пе­редачу, если: а) Рх = 3,75кВт, п_г = 1440мин-¹, /г₂ = 700 мин"¹; б) Pi =9,55кВт, «₂ = 200 мин-¹, i* = 3,7.

Ограничений габаритов и массы передачи нет, однако ее стоимость должна быть минимальной. Материал зубчатых колес: а) чугун-чугун; б) сталь-чугун.

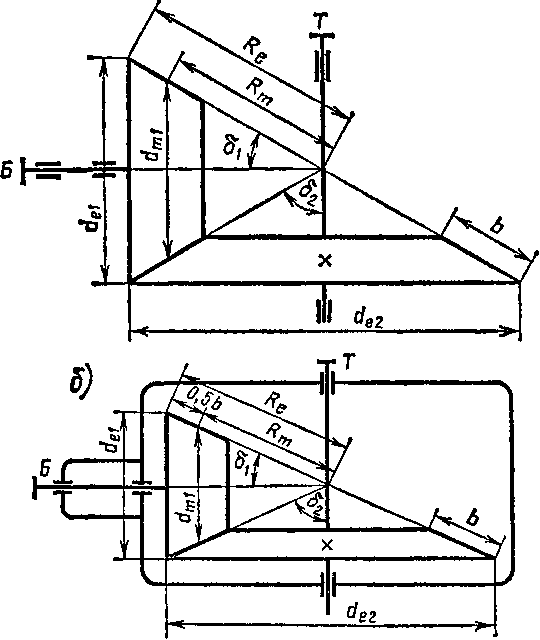
Решение, а) 1. Вычерчиваем кинематическую схему передачи (рис. 86, а), определяем передаточное отношение [см. (16)] и углы делительных конусов шестерни и колеса [см. (120)]:

i = щ/п₂ = 1440/700 = 2,06 = и; _w = tg6₂ = 2,06 и 6₂ = arc tg 2,06 = 64°07'; 6i = 2—6₂ = 90°—64°07' = 25°53'.

2. Вычисляем вращающий момент на валу шестерни:

Т_г = 9,55Р!/л! = 9,55-3,75' 10³/1440 = 24,9 Н• м.

3 . Выбираем марки материала и определяем допускаемые напряжения. По табл. П28 назначаем для изготовления зубчатых колес чугун СЧ 32—52. Допускаемые напряжения на контактную и изгибную выносливость зубьев найдем по формулам (98) и (101)

о)

(см. заня-

при K_HL = K_FL=l тие 8).

По табл. П28 для чугуна СЧ 32-52 при НВ 187...255 с°_нр = 550 МПа, N_m = \Q^f, ofp~ 115МПа—передача нере­версивная, Л/^г/7₀=10⁶.

Итак, допускаемые напря­жения:

<*нр=(у hp К ml = 550-1 = ^550 МПа, a_PP=o°FpK _Pl= 115х Х1 = П5МПа.

4. Определяем параметры передачи.

Находим коэффициенты* входящие в формулу (124): k_be = b/R_e== 0,285 (см. занятие 12); k_be и/(2 — k_be) = 0,285Х Х2,06/(2—0,285) =0,342.

0.2-0,4-

Д0,2—Д0,04\ _ 0,058-* ]*—

По табл. П29, интерполи­руя, получаем для назначаемых роликоподшипников значение коэффициента /С#з

-1,04 •1,08

=0,0116.

0,058-0,04

0,2

Следовательно, /С_яр = 1,08 —0,0116= 1,0684.

\f—v _I04j/;

V (l-k_be)k_beuo²_Hp ^r (

По формуле (124) вычисляем внешний делительный диаметр шестерни:

Юз

1,0684-24,9

е) k_beuahp (1 —0,285) 0,285-2,06 (550-10°)^

= 10⁴

⁴ ^/0,2094.10-^ = 0,0593 м = 59,3 мм.

Принимаем <^1 = 60мм.

Определяем число зубьев и находим внешний окружной модуль по формуле (114).

Из 2 = 17...22 (см. занятие 12) принимаем г_А — 20 и по формуле (120) z₂ = == «z₁ = 2,06-20 = 41. Следовательно, mt_e = d_ei/Zi = 60/20 = 3 мм—стандартное (см. табл. П23).

По формуле (116) находим внешнее конусное ^расстояние:

#_£ = 0,5m^V'lF+l=0,5 3.20У 2,06* + 1 =68,7 мм.

5. Определяем ширину венца зуба, вычисляем среднее конусное расстояние [см. формулу (121)] и уточняем значение коэффициента k_be: b = k_beR_e~ = 0,285-68,7= 19,6 мм, принимаем Ь =20мм;

R_m = R_e—b/2 = 68,7—20/2 = 58,7 мм; fy>e = 6/tf_e = 20/68,7 = 0,291 < 0,3 (максимальное).

По формуле (115) вычисляем средний окружной модуль:

Щт^Ще—Ьsin6i/Zi = 3—20sin25°53720 = 3—0,4365 = 2,5535 мм, Полученное значение тщ — 2,5635 мм округлять нельзя,

По формулам (114), (118), (119) вычисляем внешние делительные диаметры, диаметры вершин зубьев и впадин шестерни и колеса:

d_ei = mteZt = 3-20 = 60 мм, d_ml = m_tmz_x = 2,6635• 20=61,27мм; <*aei = ^dei+e cos $! = 60+ 2 - 3 cos 25°53' = 60+6 • 0,902 = 65,42 мм; d_fel^d_el—2Amtecos 6i = 60—2,4-3 0,902 = 53,52мм; d_e2 = m_tez₂ = 3-4\ = 123 мм, d_m2 = m_imz₂ = 2,5635-41 = 105 мм. d_ae^d_e2+2m_te cos 6₂ = 123 + 2-3 cos 64°07' = 123+ 6-0,426= 125,56 мм; d/e2 = d_e2—2Am_te cos 6₂ = 123—2,4-3-0,426 = 119,94 мм.

Вычисляем скорость на среднем делительном диаметре и назначаем степень точности передачи:

1>_/я = ш*т₁л₁/60 = я- 51,27-Ю-³-1440/60 = 3,86 м/с.

По табл. 2 принимаем 8-ю степень точности проектируемой передачи.

6. Вычисляем силы, действующие в зацеплении: окружная сила на среднем делительном диаметре

Ft = Pi/v_m = 3,75 • 10³/3,86 = 972 Н;

осевая сила для шестерни и радиальная для колеса [см. (122)]

F_al = F_r2 =F_t tg a sin 6_t = F_t tg20° sin 25°53' = 972-0,364-0,4365 = 154 H;

радиальная сила для шестерни и осевая для колеса [см. (123)]

F_n = F_a2 = F_t tg a cos 6* = 972 -0,364 -0,902 = 310H.

7. Производим проверочный расчет по формулам (126), (127): Z//=l,76 (см. занятие 12), 2^ = 209-10³ Па^1/2 (см. табл. П22). По формулам (96а), (129) находим Z_e = y (4--e_a)/3= |/"(4—1,7)/3=0,88, где е_а « 1,88—3,2 (1/^+1/2^)=

= 1,88—3,2 (1/22+1/94) = 1,88—3,2 (0,045 + 0,012) = 1,7. Так как для открытых передач (см. занятие 8) /C#_v=l и /(^ = 1, то коэф­фициент нагрузки ## = /^0/0^== 1,0684-1 = 1,0684. Проверяем рабочее контактное напряжение по (126):

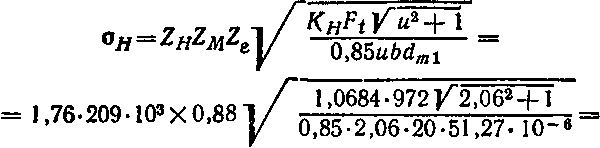
В ыносливость зубьев при изгибе проверим по формуле (127): кь_е = 0,291; k_beu/(2--k_be) = 0,291.2,06/(2—0,291) =0,351. По табл. П29, интерполируя, полу-

чаем для роликовых опор:

С

0,2—1,08 Д 0,2—Д 0,07 0,4—1,15 0,049—л:

= 0,0172.

ледовательно, K_F$ = 1,15—0,0172 = 1,133.

Итак, коэффициент нагрузки /<>=/С^/С/^ = 1,133 1 = 1,133.

При общем Ор_Р отношение OpplYp будет меньше для шестерни, так как г\ < г₂ и Y'f > Y"f (см. табл. П27) и, следовательно, проверку выносливости зубьев при изгибе выполним на шестерне.

Эквивалентное число зубьев шестерни [см. (128)]

z_vi = zx/cos б_х = 20/cos 25°53' = 20/0,902 = 22,2. По табл. П27 коэффициент формы зуба Y'f = 4,15.

Рабочее напряжение изгиба [см. (127)]

Y_FK_FF_t 4,15.1,133-972 _{1ЛК 1Лбгт} ^ о>=_А =_а ' _оп о _с~₀ ._л__в =105<10⁶Па < 0/7_Р.

^г 0,8bbmt_m 0,85*20.2,563« 10~Задача 28. Рассчитать коническую прямозубую передачу редукторного типа (закрытую) для серийного производства, если: а) Р₂ = 166кВт, «1 = 970 мин-*; я₂ = 320мин^*;б) Р₂ = 92 кВт, п₂==232 мин"⁶

¹, и = 3,15. Нагрузка переменная с не­значительными колебаниями.

При проектировании передачи желательно удовлетворить следующие требо­вания заказчика: возможность работы зуба обеими сторонами (реверсивная передача); габариты и масса передачи должны быть минимальными* а ее стои­мость —невысокой.

Решение, а) 1. Вычерчиваем кинематическую схему закрытой конической зубчатой передачи (рис. 86, б).

2. По формулам (16), (120) определяем передаточное отношение и угол де- лительного конуса шестерни 6j и колеса б_а:

/ == щ1щ = 970/320 = 3,03 = и.

Полученное значение передаточного числа согласуем с ГОСТ 12289—76

(см. четвертый раздел). К значению и = 3,03 из стандартного ряда ближе всего и = 3,15, которое и принимаем.

Из w = tg6₂ и 01+62 = 2 = 90° получаем:

6₂=arct g и = arotg 3,15 = 72°23'; 6i=2—6₂ = 90° — 72°23' = 17°37'♦

3. Вычисляем мощность на быстроходном валу проектируемой передачи. Для закрытых конических зубчатых передач при нормальной эксплуатации

и тщательном уходе КПД в зацеплении х\ = 0,95.. .0,98, принимаем щ = 0,96, Для одной пары подшипников качения т]₂ = 0 99. Общий КПД (рис 86, б)

т] = г] i г)! = 0,96«0,995 = 0,94.

Следовательно j

Pi = ^2/Л= 166/0,94 = 176,8 кВт.

4. Определяем вращающий момент на шестерне:

Т j=9,55P!Mi = 9,55 * 176,8.10³/970 = 1740 Н • м.

5. Выбираем марку материала и химико-термическую обработку зубьев; опре- деляем допускаемые напряжения.

Используя табл. П21 и П28, назначаем для изготовления зубчатых колес сталь 40X, HRC60...65, азотирование. По табл. П28 для этой стали а%р = = 950МПа, #_Яо=14«10*, о£р=215МПа (передача реверсивная), Л^₀=4«10^в. Назначаем ресурс передачи /_ч^а10⁴ ч и по формуле (100) находим число циклов напряжений:

N_HE= N_FB=:60t₄n_u ^ 60.10⁴«320 = 19,2« 10'.

Так как Nno ^и N_fb> N_FOt то значения коэффициентов долговечно-

сти по (99), (102) /Гя1=1 и J?_FI=1.

Допускаемые напряжения на контактную выносливость [см, (98)] и на вы­носливость зубьев при изгибе [см. (101)]:

о_Нр = o°hpKhl=950.1= 950МПа, o_FP=<fi?pK_FL=215.1=215 МПа.

6. Определяем параметры передачи.

Для передач с закаленными до высокой твердости рабочими поверхностями зубьев рекомендуется проектировочный расчет начинать с определения модуля [см. (125)]. Находим число зубьев и коэффициенты, входящие в формулу (125).

Из Zi = l8...30 (см. занятие 12) принимаем zi = 22; Za=wzi = 3,15»22 = 69,3< принимаем z₂ = 69; he — 0,285;

k_beu/(2—k_be) =0,285.3,15/(2—0,285) =0,523.

Интерполируя, по табл. П29 получаем для роликовых опор /С^ = 1,41. Коэффициент формы зуба находим по эквивалентному числу зубьев колеса [см. (128)]:

М = *2/cos 6_a = 69/cos 72°23' = 69/0,3187 = 216.

По табл. П27, интерполируя, получаем У>=3,77.

Коэффициент ширины венца зуба вычислим по формуле (130):

y>bd = b/d_mi=kbe/№--k_be) sin 6i] =0,285/[(2—0,285) sin 17°37' ]= = 0,285/(1,715<0,301)= 0,556. По формуле (125) вычисляем средний окружной модуль:

3,77-1,4Ы740

_Щт> 1,4₅|/^^=1,45^

222.0,556.215.10^е = 1,45 3/0,107-10~⁶ = 6,88-10-5 _м==б,88 мм. По формуле (114) находим средний делительный диаметр шестерни:

rf^i=mf_OTZi=6,88*22 = 151 мм, Ширина венца зуба по (130)

&=^&Al = 0,556.151 =84 мм. Внешний окружной модуль по (115) Ще = Щт+ (b/Zi) sin 6j = 6,88+ (84/22) 0,301 = 6,88+1,15 = 8,03мм.

По СТ СЭВ 310—76 принимаем m_te = 8 мм^т(табл. П23). Уточняем значение т\_т и по формуле (114) определяем средние делительные диаметры шестерни и колеса:

Щт = Щ_е—Ь sin 6i/z_x = 8—1,15 = 6,85 мм—округлять нельзя; dmi=ЩтЧ = 6,85.22 = 150,2мм; й_ть = m_tmz₂ = 6,85*69=452,65мм.

По формуле (116) находим внешнее конусное расстояние и уточняем значе­ние коэффициента kb_e'-

R_e=0,bm_teZiУ Ф +1 = 0,5^8• 22V 3,15? +1 =291мм; k_be = b/R_e = 84/291 =0,289<0,3.

По формулам (114), (118), (119) вычисляем внешний делительный диаметр, средний делительный диаметр и диаметры вершин и впадин зубьев шестерни и колеса:

а) для шестерни

d_ei=m^i = 8.22 = 176MM, d_/wi = mf_Wz₁=6,857«22= 151 мм; *ael = d_e\+2m_te cos 6j = 176 + 2.8 • cos 17°27' = 176 +16 •0,954 = 191,25 мм; d/el=d_ei—2_t4tnt_e ^c°s fy= 176—2,4«8.0,954= 157,65 мм;

б) для колеса

й_ег — Ще*ъ* ^<?2=б60мм, ^2=^^22=6,857«70 = 480 мм; daeb=d&+2m_te cos 6_a=560 + 2 • 8 cos 72°33' = 560 +16 • 0,3=564,8 мм; d/eu = d_es—2,4/Wf,, cos 6a = 560—2,4«8^0,3 = 554,24 мм,

7. Назначаем степень точности передачи.

Скорость точки на среднем делительном диаметре шестерни

v_m =лй_1Я1_п1/60=л. 150,2-10-3.970/60=7,66 м/с.

По табл. 2 при v_m=7,66 м/с принимаем 7-ю степень точности передачи,

8. Вычисляем силы, действующие в зацеплении:

окружная сила на среднем делительном диаметре

Ft^PilVm^ 176,8-10³/7,66=23,1 • 10³ Н = 23,1 кН; осевая сила для шестерни и радиальная для колеса по (122) F_ai=:F_ru = Ft tg a sin 6i=F_t tg 20° sin 17^e27' =23,1 '0,364.0,3=2,53 кН; радиальная сила для шестерни и осевая для колеса по (123)

F_n=F_a2=F_ttga cos 61=23,1.0,364 »0,954 = 8,02 кН.

Проверку запроектированной передачи на контактную [см. (126)] и изгибную [см. (127)] выносливость зубьев рекомендуем выполнить учащемуся самостоятельно.

Литература: [1, 3, 6, 10, 11]; задачи: 9.37, 9.45, 9.56, 9.58 [12].

Вопросы для самопроверки. 1. Каково основное различие между фрикцион­ными и зубчатыми передачами? 2. Укажите достоинства и недостатки зубчатых передач по сравнению с фрикционными, ременными и цепными (см. занятия 2, 4, 7). 3. Что такое эвольвента окружности и как производится построение этой кривой? (См. занятие 7). 4. Сформулируйте основную теорему зацепления (см. за­нятие 7). 5. Дайте определение всем основным геометрическим параметрам эволь-вентного зубчатого зацепления (см. занятие 7). 6. Какие окружности зубчатых колес и в каких случаях называют начальными и делительными? Укажите за­висимость между модулем и делительным диаметром (см. занятия 7 и 8). 7. Что такое коэффициент перекрытия и как он влияет на работу зубчатой передачи? (Занятие 7). 8. Укажите основные методы нарезания зубьев и дайте их сравни­тельную характеристику (см. занятие 7). 9. Укажите основные виды разрушения и повреждения зубьев (см. занятие 7). 10. Какова связь между торцовым и нор­мальным модулями? (см. занятие 9). 11. В чем состоит основное различие рас­чета открытых и закрытых зубчатых передач? (см. занятие 8). 12. Почему откры­тые зубчатые передачи не рассчитывают на выносливость рабочих поверхностей зубьев по контактным напряжениям? (см. занятие 8). 13. Почему не рекомендуется принимать число зубьев шестерни менее 17? (см. занятие 8). 14. Почему рекомен­дуется принимать для шестерни материал лучшего качества, чем для колеса? (см. занятие 8). 15. Какой модуль непрямозубой передачи обычно стандартизован и почему? (См. занятие 10). 16. Какие силы возникают в зацеплении цилиндри­ческих косозубых колес, конических прямозубых колес? По каким формулам вычисляют эти силы? (См. занятия 8, 10 и 12). 17. Какие передачи, прямозубые или непрямозубые, предпочтительно применять при высоких скоростях и почему? (См. занятие 10). 18. При выполнении проектировочного расчета какой параметр зубчатой передачи определяется из условия контактной выносливости и какой — из условия выносливости зуба на изгиб? 19. От чего зависит значение коэффи­циента формы зуба? (См. занятие 8). 20. Укажите зависимость между средним и [максимальным модулями конической прямозубой передачи (см. занятие 12). 21, Как изменяется высота зуба конической прямозубой передачи в поперечных сечениях, проведенных на разных расстояниях от вершины конуса? (См. заня­тие 12). 22. От чего зависит выбор степени точности зубчатой передачи? (Заня­тие 8 и табл. 2). 23, Зависит ли прочность зуба на изгиб от размера модуля? 24. По какому числу зубьев выбирают значение коэффициента формы зуба для непрямозубых цилиндрических и прямозубых конических зубчатых колес? (См. занятия 10 и 12).

Занятие 14. ПЕРЕДАЧА ВИНТ —ГАЙКА Винтовая линия, винтовая поверхность и их образование

Если прямой круговой цилиндр огибать прямоугольным тре­угольником (рис. 87) так, чтобы точки одного из катетов АС сов­падали с соответствующими точками окружности nd_u основания цилиндра, то гипотенуза АВ опишет на боковой поверхности ци­линдра винтовую линию. Угол, образованный гипотенузой АВ₉

5*

131

я вляющейся разверткой винтовой линии, и катетом АС,— развертка окружно­сти основания цилиндра — называется углом подъема винтовой линии ф. Рас­стояние АВ между двумя соседними точками винто­вой линии, лежащими на одной из образующих ци­линдра, называется шагом Р винтовой линии.

Если геометрическую фигуру (треугольник, пря­моугольник , тра пецию, сегмент и т. д.), лежащую в одной плоскости с осью цилиндра, вращать вокруг его оси так, чтобы любая из точек основания фигуры скользила по винтовой линии (рис. 88), то контурные линии заданной фигуры опишут винтовую поверхность.

Рис. 88

Резьба, профили резьб и основные элементы винтовой пары

Терминология, символика и основные определения параметров резьбы регламентированы ГОСТ 11708—66 „Резьбы, основные опре­деления".

Поверхность, образованная при винтовом движении плоского контура (треугольника, трапеции и т. д.) по цилиндрической или

конической поверхности, называется резь-

О) ПЧ —-reass^m^ ^бой- Р^езьба, образованная на цилиндриче-

ff\ 1 ской (конической) поверхности, называет-

V/ ' ся цилиндрической (конической).

jt* Цилиндр или конус, боковая поверх-

"J/1 ность которого переходит в винтовую

поверхность, называется винтом—ци- линдрическим (рис. 89, а) или кониче- Рис 89 ским (рис. 89, б). Один оборот резьбы (вин-

товой линии) на боковой поверхности цилиндра (конуса) называется витком.

Контур сечения резьбы в плоскости, проходящей через ее ось (ось винта), называется профилем резьбы. Очевидно, профилем резьбы

я вляется та фигура, при винтовом движении которой образуется резьба. На рис. 90 показаны пять основных профилей резьбы: а—треугольная; б—упорная; б—трапецеидальная; г —прямоуголь-

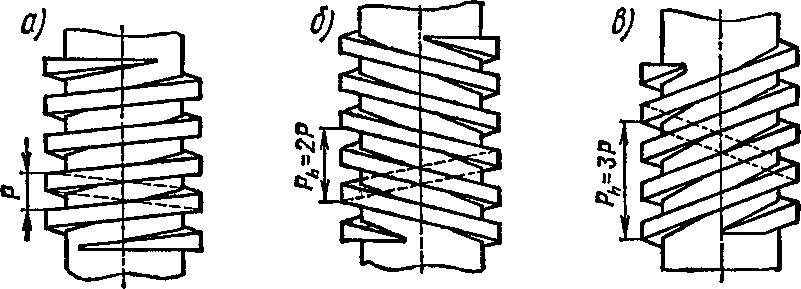
н ая; 9—круглая. Из них наибольшее распространение в машино-и приборостроении получил** треугольная (крепежная резьба) и трапецеидальная (ходовая, т. д. предназначенная для передачи силы и движения,—винты прессов, домкратов, станков и т. д.).

Расстояние между соседними одноименны­ми боковыми сторонами профиля в направлении, параллельном оси резь­бы, называется шагом резьбы. Шаг резьбы, как и шаг винтовой линии, обозначают Р (см. рис. 88).

Если на видимой части цилиндра (конуса) винтовая поверхность поднимается слева направо, то резьбу называют правой (рис. 91, а, в), а если справа налево, то левой (рис. 91, б).

Резьбу нарезают (рис. 92, а) или накатывают (рис, 92, б) на цилиндрическом (коническом) стержне резьбонарезным инструментом (резец, плашка, фреза, гребенка, ролики). Если окружность осно­вания цилиндра (окружность торца заготовки для винта) разделить на несколько равных частей (две, три, четыре и т, д., рис, 93) и

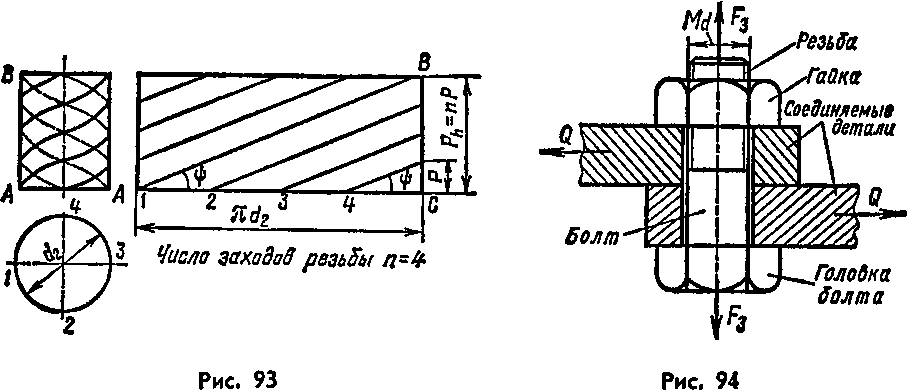
затем из размеченных точек нарезать резьбу, то на теле винта (болта) образуется двух, трех- и четырехзаходная резьба. На рис, 91 показаны однозаходная (а), двухзаходная (б) и трехзаходная (в) резьбы.

Многозаходная резьба характеризуется шагом Р и ходом P_h. Расстояние между ближайшими одноименными боковыми сторонами профиля, принадлежащими одной и той же винтовой поверхности в направлении оси резьбы, называется ходом резьбы Р^ (рис, 91, 93). Для однозаходной резьбы понятия шага и хода совпадают.

Для многозаходных резьб ход равен произведению числа захо­дов п на шаг резьбы:

Рн=пР. (132)

Угол, образованный касательной к винтовой линии в точке, лежащей на среднем диаметре резьбы и плоскостью, перпендику­лярной оси резьбы, называют углом подъема резьбы и обозначают «ф.

Из ДЛВС (см. рис. 87 и 93) установим зависимость между углом подъема винтовой линии, средним диаметром резьбы и ее ходом:

tg * =s P_h!(nd₂) = nP/(nd₂). (133)

Деталь с резьбовым отверстием называют гайкой (рис. 94). Если винт и гайка имеют резьбу одного профиля с соответственно рав­ными параметрами, то они образуют кинематическую винтовую пару, которая обладает следующими свойствами:

при повороте винта на один оборот, если неподвижна гайка, винт кроме вращательного получает также поступательное движе­ние, перемещаясь вдоль оси на один ход резьбы; при повороте гайки на один оборот, если неподвижен винт, гайка кроме вращательного получит также поступательное движение, перемещаясь вдоль оси винта на один ход резьбы. При увеличении угла подъема винтовой линии происходит возрастание шага Р (или хода P_h для многоза-ходных резьб), т. е. при одном обороте гайка проходит большее расстояние вдоль оси винта (или винт проходит больший путь от­носительно неподвижной гайки).

В тех случаях, когда по условиям работы винтовой пары тре­буется, чтобы винт (или гайка) имел большее перемещение за один оборот, применяют многоза-ходную резьбу. Конечно, та­кую же кинематику может иметь и однозаходная резь­ба, если ее шаг равен ходу многозаходной резьбы. Но при этом в пределах высоты гайки будет мало витков резьбы (либо надо делать очень высокую гайку) и ее п рочность недостаточна. Многозаходная резьба обес­печивает большие перемеще­ния (за один оборот) при достаточной прочности резь­бы.

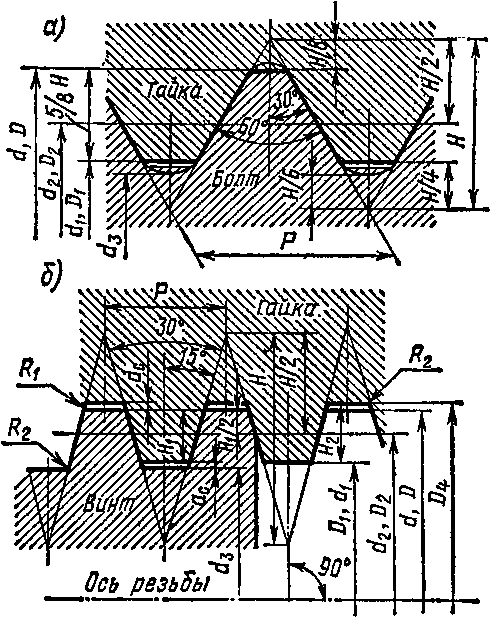
Кроме профиля, шага, хода и угла подъема вин­товой линии винтовую пару характеризуют следующие параметры (рис. 95):

наружный диаметр резь-бы d = D—диаметр вообра­жаемого цилиндра, описан­ного вокруг вершин наружной резьбы или впадин внутренней резьбы. Этот диаметр является номинальным диаметром резьбы винта (d) и гайки (D);

внутренний диаметр резьбы d^Dj —диаметр воображаемого цилиндра, вписанного во впадины наружной резьбы (dj) или в вер­шины внутренней резьбы (D_x); ^—внутренний диаметр болта (винта) По дну впадины;

средний диаметр резьбы d₂ = D₂—диаметр воображаемого соос-ного с резьбой цилиндра, образующая которого пересекает профиль резьбы в точках, где ширина канавки равна половине номиналь­ного шага резьбы, т. е. при отсутствии погрешностей резьбы обра­зующая указанного цилиндра пересекает профиль резьбы в точках, где ширина выступа равна ширине ее канавки.

За расчетную площадь поперечного сечения метрической и тра­пецеидальной резьбы принимают площадь расчетного сечения диа­

метром d_it т. е.

Основные параметры резьбы d, d_i% d_u, d₈, P (рис. 95) указаны в таблицах стандартов (см. табл. ПЗО, ГШ).