Основные геометрические соотношения

Так как зубья на боковых поверхностях конусов отличаются от зубьев цилиндрических колес тем, что их размеры (толщина, высота —см. рис. 73 и 74) по мере приближения к вершине конуса уменьшаются, то соответственно изменяются шаг и модуль зацеп­ления, а также и диаметры делительной, вершин и впадин зубьев. Очевидно, в торцовых сечениях зубчатых колес, соответствующих их наибольшим диаметрам, шаг и модуль зацепления также наибольшие.

Основные параметры зацепления конической прямозубой пере­дачи выражаются через модуль:

^{dm = mtmz и de — mtezt (114)}

где d_m — средний делительный (начальный) диаметр шестерни (d_mX) или колеса (d_m2); d_e — внешний делительный (начальный) диаметр (диаметр основания делительного конуса) шестерни (d_el) или колеса (d_e2); г —число зубьев шестерни или колеса; tn_tm — средний окружной модуль; m_ie—внешний окружной модуль, значения кото­рого обычно согласуют с СТ СЭВ 310—76 (см. табл. П23).

Между модулями m_tm и m_te существует зависимость (рис 74)

^{mim = ти (1 — 0,5ЛЬ,) = mte — b sin bjz„ (115)}

где k_be = b/R_e — коэффициент ширины зубчатого венца; &—ширина зубчатого венца (длина зуба), измеренная параллельно образующей делительного конуса.

Внешнее конусное расстояние

R_e = m_tez_x/(2 sin Ь_х) = 0_$5m_tez_x Vtt²+l. (116)

Размер модуля т_и определяет выбор параметров режущего инструмента; обычно значение т_и выбирают из ряда стандартных модулей, хотя это и не обязательно.

Высоту головки h_ae и ножки h_fe зуба принимают

в

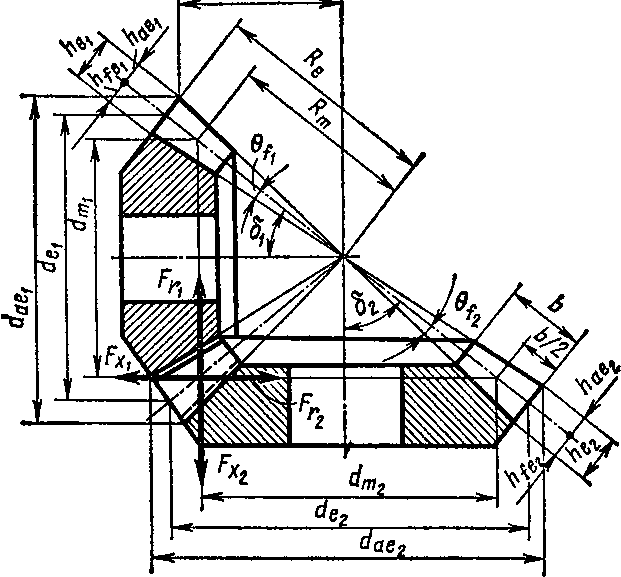
Рис. 74

Согласно рис. 74, диаметры вершин зубьев и впадин конического зубчатого колеса соответственно равны:

d_ae = d_e + 2h_ae cos б = d_e + 2m_u cos 6, (118)

d_fe = d_e — 2h_fe cos 6 = d_e — 2_$4m_te cos 6. (119)

Передаточное число при 2 = 90° [см. формулы (86), (114), (16) и рис. 73,6]

и = г_%1г_х=*й_мг1й_ш1 = tg8₂ = ctg Ъ_х = щ/щ = /. (120)

Среднее конусное расстояние

^ = ^-0,56. (121)

Силы, действующие в зацеплении

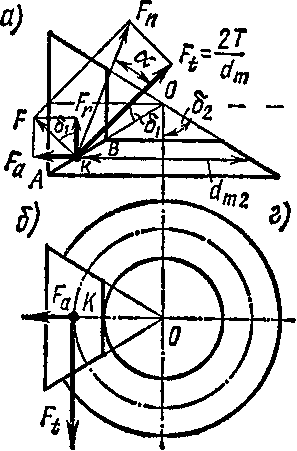
При работе прямозубой конической передачи сила давления F_n зуба шестерни на зуб колеса действует по нормали к боковой поверхности зубьев, находящихся в зацеплении. Силу давления F_n в точке К (рис. 75, а), являющуюся равнодействующей параллель­ных сил, действующих на контактную линию пары зубьев, разложим

на две составляющие: F_tt направленную по общей касательной к среднему диаметру шестерни и колеса, и F, перпендикулярную вектору F_t.

F_n = F_t+F-—нормальная сила, действующая на боковую поверхность зуба и направленная по линии зацепления; F_t =

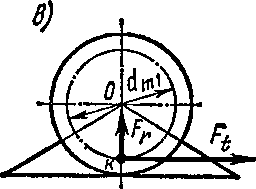
= F_ncosa = 2T/d_m —ок­ружная сила; а = 20° — угол главного профиля (зацепления).

С

F*lF_alF„

^4	'/>/ |\ ~/™\\

оставляющую F, в свою очередь, разло­жим на силы F_r и F_e, как показано на рис. 75, а или г:

F = F_r + F_a.

Сила F_a является осевой для шестерни, а равная ей и противопо­ложно направленная си­ла — радиальной для ко­леса:

F_al = F_r2 = Fsin б_х =

= F_/tgccsin6₁> (122)

Аналогично, сила F_r —радиальная для шестерни, а равная ей и противоположно направленная сила —осевая для колеса:

F_r1 — F_a2 = F cos 8, = F, tg a cos 8_A. (123)

Наличие в передаче осевых сил требует надежного осевого креп­ления валов шестерни и колеса относительно оси вала.