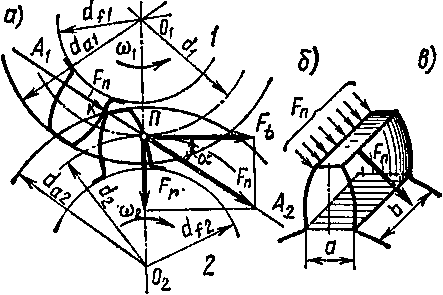
Силы, действующие в зацеплении

При работе цилиндрической прямозубой передачи сила давления F_n ведущей шестерни 1 в начале зацепления передается ножкой зуба на сопряженную боковую поверхность (контактную линию) головки зуба ведомого колеса 2 (рис. 65, а).

При точном изготовлении и монтаже сопряженных зубчатых колес^ сила давления F_n равномерно распределена по ширине венца зуб­чатого колеса и направлена (в предположении отсутствия трения)

о с)	А	к*
						гь
			a i
				п

по общей нормали (линии зацепления A_tA₂) к соприкасающимся боковым поверхностям зубьев (рис. 65, б).

Перенесем точку приложения К силы давления F_n по линии зацепления А_ХА₂ в точку Я— полюс зацепления (рис. 65, а). Раз­ложим силу Р_п на две составляющие: F_i9 направленную по общей касательной к делительным окружностям шестерни и колеса, и F_n направленную по линии центров О_х0₂, тогда

F„ = F_t + F_r

Здесь окружная сила, изгибающая зуб, F_t = F„cosa-27/rf.

Радиальная (распорная) сила, сжимающая зуб, F_r = F_nsina = F_ttga,

(88)

(89) 91

Расчет зубьев на контактную и изгибную выносливость

При расчете зубьев на контактную выносливость исходят из следующих положений: а) силу нормального давления F_n=Q счи­тают приложенной в полюсе зацепления Я (рис. 65, a) F_n = F_t/cosa; б) зубья рассматривают как цилиндры с образующей длиной Ъ и радиусами кривизны p₁ = 0,5d₁sina; p₂ = 0,5d₂sina = 0,5wd₁sina. Для непрямозубой передачи (см. ниже) форма косого зуба в нор­мальном сечении определяется эквивалентным прямозубым колесом, диаметр которого d_v = d/cos²$, а суммарная длина контактной линии Ъ* = /s==fce_a/cosp_b. Приведенный радиус кривизны (см. занятие 2)

р1р₂ 0,5с?х sin a-0,5aV* sin a d\U sin a _t

^Рпр ~ Pi+ P2 — 0,56?i sin a (1 + u) — 2(u+1) в) неточности изготовления и монтажа передачи, деформации зубьев и валов приводят к неравномерному распределению на­грузки F_n по длине l = b контактной линии и нарушению плавно­сти зацепления —зубья входят в зацепление с ударом. Поэтому для обеспечения необходимой прочности зубьев и нормальной работы передачи в расчетные формулы вводят не номинальное значение F_u а расчетное F_fv = K_HF_t, где K_h = Kh$K_Hv^ 1 — коэффициент нагрузки.

Заменяя в формуле (21) Q = F_n (с учетом коэффициента на­грузки К_И), подставляя значение р_пр, выполняя действия, аналогич­ные выводу формулы (23) и используя формулы (95), (96), (96а), получим в соответствии с ГОСТ 21354—75 следующую общую фор­мулу для выполнения проверочного расчета на контактную вынос­ливость зуба закрытой цилиндрической передачи и передачи с низкой и средней твердостью рабочих поверхностей зубьев:

<j_H=7_HZ_MZ_eVK_HF_t (а ± l)/(<t№)£<*hp< (90)

Выразив в неравенстве (90) F_t через крутящий момент 7\(Н-м) и Ь через %_aa_w, после возведения в квадрат, усреднения ряда ве­личин и объединения их коэффициентом К_а получим следующую формулу для определения межосевого расстояния a_w(u) при про­ектировочном расчете закрытой цилиндрической передачи и передачи с низкой и средней твердостью активных поверхностей зубьев:

a_w> К_а (а ± 1) (91)

Значения коэффициента К_а для различных материалов колес при­ведены в табл. П22. Знак плюс соответствует внешнему зацеплению, знак минус —внутреннему.

Расчет зуба на выносливость при изгибе производится в предпо­ложении, что в зацеплении находится одна пара зубьев и силы трения отсутствуют. При расчете зуб (рис. 65, б, в) рассматриваем как консольную защемленную балку, нагруженную на конце нор­мальной силой F_n = /ycosa, с опасным сечением S = ab у основа­ния (W_x = ba^;

²/6 — момент сопротивления). Перенеся силу Т_п на ли­нию симметрии зуба и разложив на две составляющие: T_n = ~F_t-\-T_n получим силу F_t = F_ncos<x, изгибающую зуб, и силу /⁷_r = /⁷_nsina, сжимающую его.

Так как усталостный излом начинается в области растянутых волокон зуба и картина напряженного состояния усугубляется зна­чительной концентрацией напряжений у его корня (зависит от ра­диуса выкрутки), то, пренебрегая силой F_r и учитывая теоретический коэффициент концентрации нагрузки /С_т, окружную силу F_t > F\ и выражая плечо / момента силы F\« F_t и размер а через модуль: /=|Ш, а = ут (|л, у — коэффициенты пропорциональности), получаем

_ М_и _ /f_TF// К^цхт _6/(_Tfx Fj _Y_FF_t ^ ^F~~ W_x~ ba²/6 ~~ b (ym)²/6 ~ y² bm ~~ bm ^ ^FP*

где Y_F= 6/С_т[г/7? — коэффициент формы зуба (см. ниже).

Итак, вводя коэффициент нагрузки K_F, получим формулу для проверочного расчета открытых прямозубых цилиндрических передач и передач с низкой и средней твердостью активной поверхности зубьев на их выносливость при изгибе:

a_F= Y_FK_FF_tl(bm)^a_FP. (92)

Принимая fe/di==^ и заменяя в уравнении (92) & = ip_wd₁; d_x = = mz_t\ F_t^=2T_i/d₁\ K_f^\AKf^ (K_Fvtt\A) и решая его относи­тельно т, получаем формулу для проектировочного расчета откры­тых цилиндрических передач и передач с высокой твердостью активных поверхностей зубьев:

т>К_тУ Y_fKf$ ТЛгЩмОп). (93)

Для прямозубых передач 1,4.