Зацепление двух эвольвентных зубчатых колес

Эвольвентой или разверткой окружности называют кривую ЛД^ЛзДд (рис. 54, а), описываемую точкой А прямой АВ, лежащей в плоскости круга и перекатывающейся без скольжения по его окружности радиуса г_ь. Окружность диаметра d_b называют основной окружностью эвольвен-

Эволь-получить способом:

Нграстями* мая нить

т ы AA_tA₂A₃. венту можно еще и таким к концу нерастяжимой нити, намотанной в один слой на боковую по- _м верхность неподвижно­го кругового цилиндра, прикрепить острие ка­рандаша и провести линию по листу бумаги, лежащему в плоскости

разматывания нити и перпендикулярному оси цилиндра (рис. 54, б).

Профилирование боковой поверхности зубьев по эвольвенте впер­вые было предложено знаменитым математиком Леонардом Эйлером в 1754 г.

Зубья, профиль которых очерчен эвольвентой (рис. 55), относи­тельно легко, просто и точно могут быть нарезаны на зуборезных станках простейшим режущим инструментом —гребенкой (инстру­ментальная рейка, см. ниже) с прямолинейными режущими кром­ками. Эвольвентная система зацепления обеспечивает высокую проч­ность зубьев, простоту и удобство измерения параметров зацепления, взаимозаменяемость зубчатых колес при любых передаточных отно­шениях.

На рис. 56 показано силовое давление F_n зуба шестерни 1 на зуб колеса 1'\

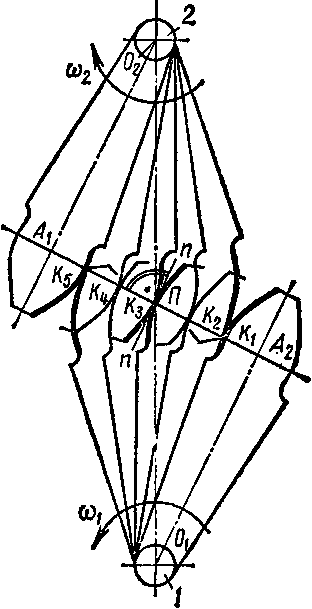
На рис. 57 показана последовательность контакта точек про­филя (контактных линий) боковых поверхностей пары сопряженных зубьев в процессе их зацепления. От начала зацепления (точка К± профиля ножки зуба ведущего колеса /) и до его конца (точка К_ъ ножки зуба ведомого колеса 2) сила давления зуба ведущего колеса / на точки (линии) боковой поверхности зуба ведомого колеса 2 на­правлена по прямой А_гА₂, нормальной к профилю зуба в контакт­ных точках Ki,K₂,K₃ и называемой линией зацепления.

Непрерывное зацепление при вращении зубчатых колес с по­стоянным передаточным отношением возможно только в случае очер­чивания профиля зуба по кривой, подчиняющейся основной теоре­ме зацепления: общая нормаль (линия зацепления A_tA₂, см. рис. 55.. .57) к сопряженным профилям зубьев делит межосевое расстояние (a_w = O_x0₂) на отрезки (О_гП и 0₂#), обратно пропорциональные угловым скоростям щ и о>₂.

Если положение точки Я, называемой полюсом зацепления, не­изменно в любой момент зацепления, то передаточное отношение

OJ1IOJI = оуох, = I = const. (78)

Если положение полюса зацепления Я будет изменяться на не­изменном отрезке линии центров О_г0_2> то согласно формуле (78) передаточное отношение не будет постоянным.

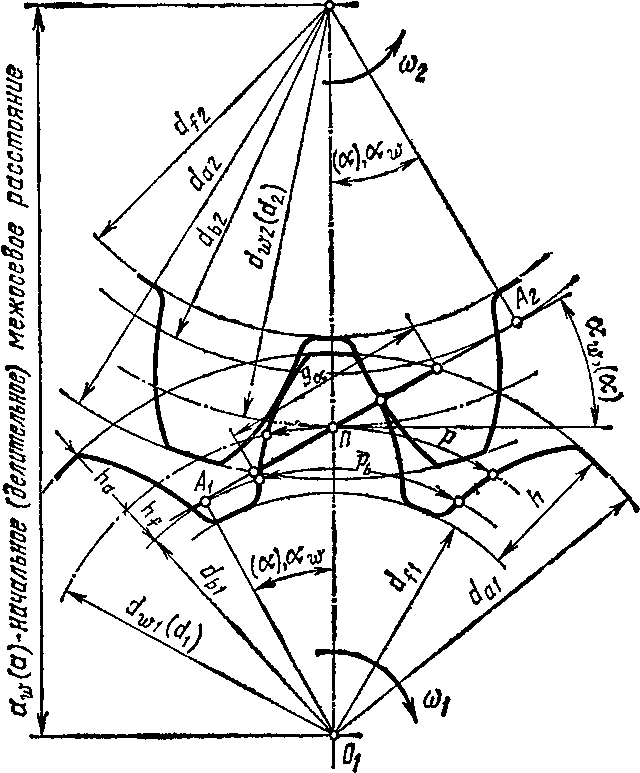
Рис. 55

Окружности, касающиеся друг друга в полюсе зацепления, име­ющие общие с зубчатыми колесами центры и перекатывающиеся одна по другой без скольжения, называют начальными (см. рис. 55); их диаметры обозначают d_wi и d_w2.

При изменении межосевого расстояния a_w=O_x0₂ пары зубчатых колес меняется и положение полюса зацепления Я на линии цент­ров О_х0₂, а следовательно, и размер начальных диаметров зубчатых колес, т. е. у пары сопряженных зубчатых колес может быть бес­численное множество начальных окружностей. Заметим, что понятие «начальные окружности» относится лишь к паре сопряженных зуб­чатых колес; для отдельно взятого зубчатого колеса нельзя говорить о начальной окружности.

Е сли заменить одно из колес зубчатой рейкой (рис. 58), то для каждого зубчатого колеса найдется только одна окружность, катя­щаяся по начальной прямой CD рейки без скольжения; эта окружность называ­ется делительной.

В дальнейшем рассматриваются толь­ко такие зубчатые передачи, у которых начальные и делительные окружности зубчатых колес совпадают.

Так как у каждого зубчатого колеса имеется только одна делительная окруж­ность, то она и положена в основу оп-

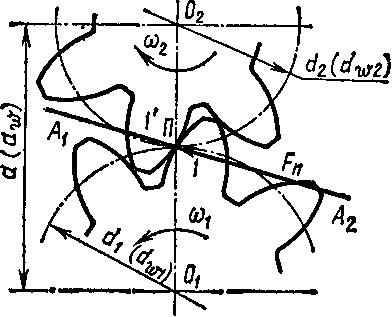
Рис. 56

ределения основных параметров зубчатой передачи; ее диаметр обо­значают d (см. рис. 55).

Окружность, ограничивающую высоту зубьев, называют окруж­ностью вершин зубчатого колеса; ее диаметр обозначают d_a. Окруж­ность, ограничивающую впадины зубьев, называют окружностью впадин зубчатого колеса; ее диаметр обозначают d_f.

Часть профиля зуба, ограниченная делительной окружностью и окружностью выступов, называется головкой зуба; высоту головки зуба обозначают h_a. Часть профиля зуба, ограниченная делительной окружностью и окружностью впадин, называется ножкой зуба; высоту ножки зуба обозначают h_f. Высота зуба

h = h_a + h_f.

Между диаметрами основной d_b и делительной d окружностей существует зависимость

d_b = d cos а. (79)

Прямая линия Л₁Л₂, проходящая через полюс зацепления 77 касательно к основным окружностям шестерни (зубчатое колесо с меньшим числом зубьев) и колеса (зубчатое колесо с большим числом зубьев), называется линией зацепления.

Линия зацепления является линией давления сопряженных профи­лей зубьев в процессе эксплуатации зубчатой передачи.

Угол a_wy образованный линией зацепления A_tA₂ и общей каса­тельной, проведенной через полюс зацепления к делительным (на-

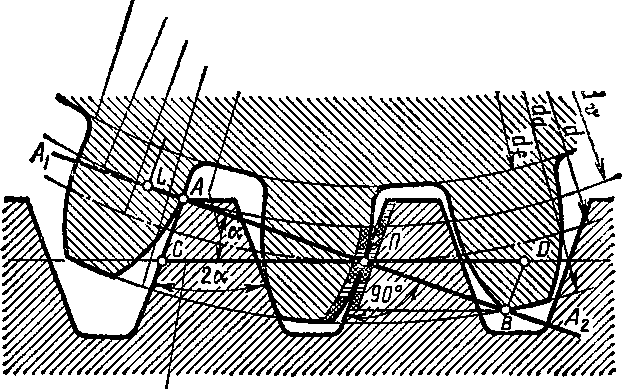
О кружность впадин зубчатого шева Основная окружность ' Делительная окружность Окружность дершин зу$ъев Угол профиля <х-20*

чальным) окружностям шестерни и колеса, называется углом за­цепления.

Угол профиля зуборезного инструмента а по СТ СЭВ 308—76 равен 20°. Следовательно, при a = a_w

а = а^ = 20°.

Отрезок g_a линии зацепления, ограниченный окружностями вы­ступов шестерни и колеса, называется активной частью линии за­цепления или длиной зацепления. Длина зацепления определяет начало и конец зацепления пары сопряженных зубьев (см. рис. 55).

Путь, проходимый точкой профиля зуба по делительной (началь­ной) окружности за время его фактического зацепления, называется дугой зацепления.

Расстояние между одноименными профилями двух соседних зубьев, взятое по дуге делительной (основной) окружности, называется ок­ружным шагом по делительной p_t или основной р_ъ окружностям. Для сопряженной пары зубчатых колес шаг p_t шестерни и колеса одинаков и равен шагу производящей (инструментальной) рейки. Между р_ь и p_t существует зависимость

p_b = p_t cos а. (80)

Отношение длины зацепления g"_a к окружному шагу р_ъ по основ­ной окружности называется коэффициентом торцового перекрытия г_а:

е_а = ga/рь = ga/(Pt cos a). (8 i)

Для непрерывной нормальной работы зубчатой передачи необхо­димо, чтобы длина зацепления была больше окружного шага р_ь:

ёа>Рь и e_a=g_a/(p*cosa)> 1.

Если e_a> 1, то до выхода из зацепления, одной пары зубьев к линии зацепления подходит другая пара зубьев —это и обеспе­чивает непрерывность зацепления и плавность хода передачи. При г_а < 1 передача нормально работать не будет, так как при выходе из зацепления одной пары зубьев другая пара не попадает на ли­нию зацепления и непрерывность вращения зубчатых колес нару­шается, т. е. в этом случае произойдет перерыв в зацеплении, от­носительные окружные скорости зубчатых колес изменятся и за­цепление следующей пары зубьев будет сопровождаться ударом. При е_а=1 передача может нормально работать только теоретически.

Значение коэффициента перекрытия показывает, сколько пар зубьев в среднем одновременно находится в зацеплении. При 1 < < е_а < 2 одна пара зубьев непрерывно находится в зацеплении, причем в начале и конце зацепления любой пары зубьев на линию зацепления подходит вторая пара зубьев; таким образом, в зацеп­лении уже находятся две пары зубьев. Если 2 < г_а < 3, то две пары зубьев непрерывно находятся в зацеплении, а в начальном и ко­нечном периодах зацепления—три пары зубьев.

Минимально допустимые значения коэффициента перекрытия за­висят от точности изготовления и сборки зубчатых колес. Так, для зубчатых колес, изготовленных по 6-й степени точности, eSⁱⁿ = 1,05, ло 7-й степени точности — е$^,п = 1,08, по 8-й степени точности — e£ⁱⁿ= — 1,15, по 9-й степени точности — е£^1п= 1,35.

Чем больше коэффициент перекрытия, тем большее число пар зубьев одновременно находится в зацеплении и тем плавнее и спокой­нее работа передачи. У прямозубых колес 1<е_а<2, у непрямо­зубых е_а может быть значительно больше.

Так как длина делительной окружности равна произведению окружного (торцового) шага p_t на число зубьев г: nd = p_tz, то

d= (p_t/n) z = m_tz, (82)

где m_t = p_t/n = d/z--окружной модуль зубьев, являющийся основным параметром зубчатой передачи.