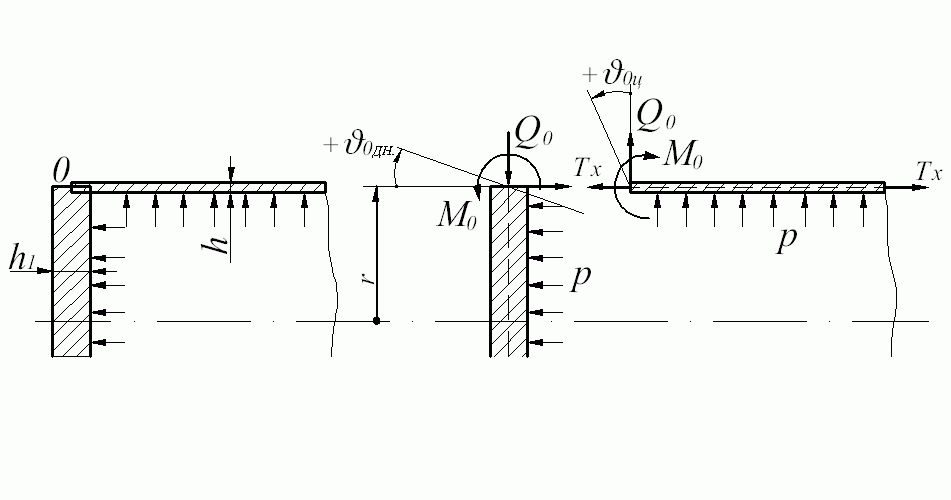Решение.
Так как днище весьма толстое, то край оболочки будем считать жестко заделанным. Запишем граничные условия:
при
;
при
.
Осевое усилие в данном случае
.
Согласно граничным условиям, с учетом зависимостей (13.114) и (13.115) получим два уравнения:
;
,
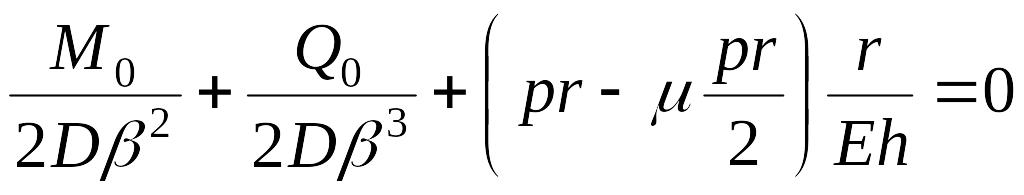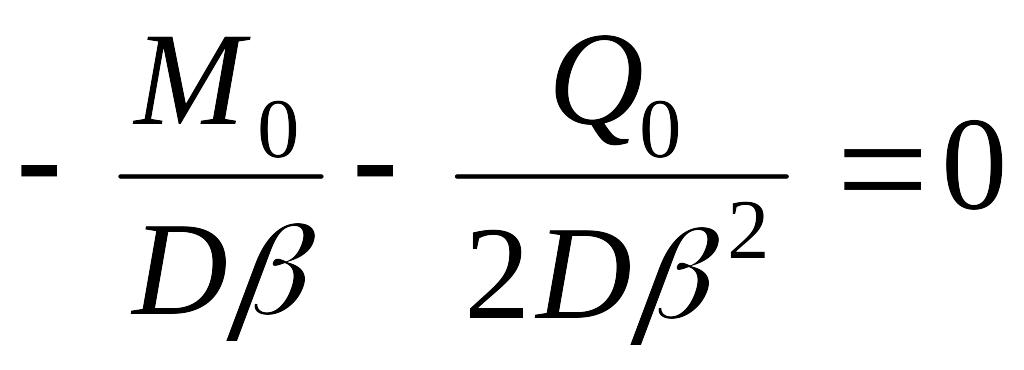решив которые, найдем
;
.
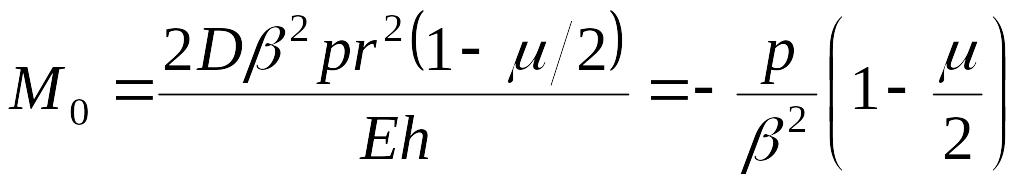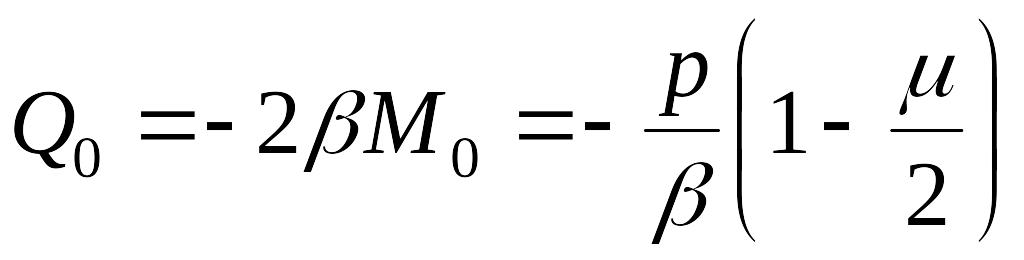Далее, по формулам (13.114)–(13.118) определяем радиальное перемещение и внутренние силовые факторы:
;
;
.
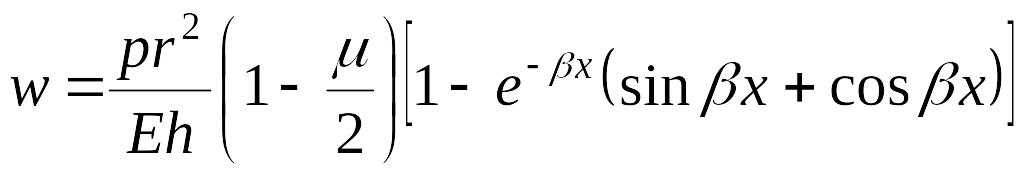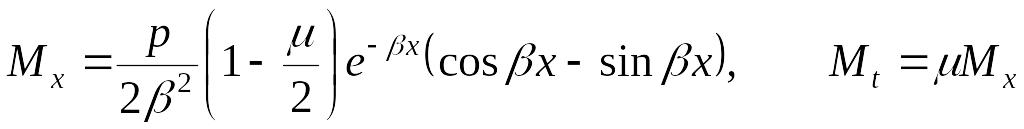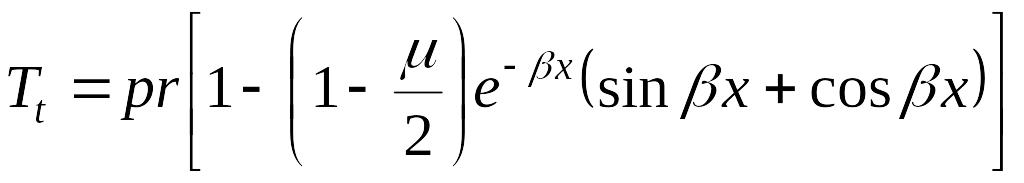На рис. 13.35, б
приведены эпюры
,
и
,
построенные при следующих числовых
данных:
.
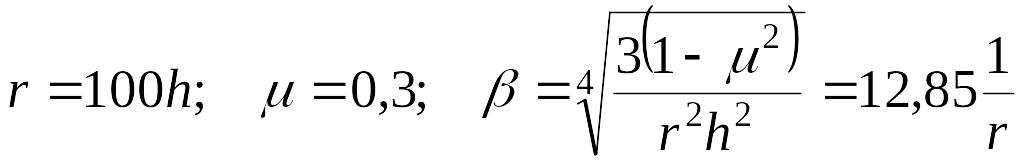Наибольшие изгибающие моменты возникают при :
;
.
Растягивающие усилия при :
Напряжения в опасной точке у заделки:
;
;
.
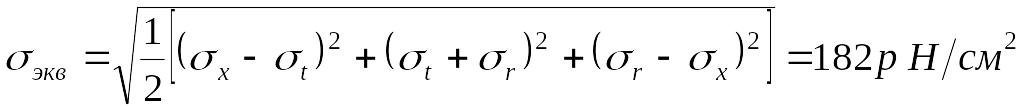В сечениях цилиндра, удаленных от заделки, изгибающие моменты обращаются в нуль, а растягивающие усилия принимают значения
; 
Соответствующие им напряжения
;
;
.
Результаты расчета
показывают, что эквивалентное напряжение
в сечении у заделки в 2 с лишним раза
больше, чем вдали от заделки. Зона
изгибных напряжений, однако, очень мала
и на расстоянии
от заделки изгибные напряжения уже
обращаются в нуль.
Пример 13.9. Определить напряжения в цилиндре, рассмотренном в предыдущем примере, считая, что днище имеет толщину, соизмеримую с толщиной стенки цилиндра.
Решение.
Отделим мысленно
цилиндр от днища, как показано на рис.
13.36, а, и примем точку пересечения
срединных поверхностей
за точку сопряжения. Такой способ
разделения позволяет записать условия
сопряжения в наиболее простой форме.
|
|
а |
б |
Рис. 13.36. К примеру 13.9
Осевую силу в цилиндре определим из условия равновесия днища:
Остальные два силовых фактора в сечении должны быть определены из условий совместности деформаций цилиндра и днища:
при
(деформацией растяжения днища
пренебрегаем);
при
.
Направления отсчетов углов, принятые за положительные, указаны на рис. 13.10, б.
Перемещения края цилиндра, согласно зависимостям (13.114) и (13.115),
;
.
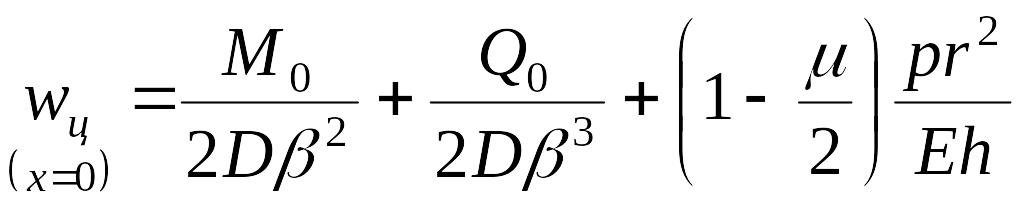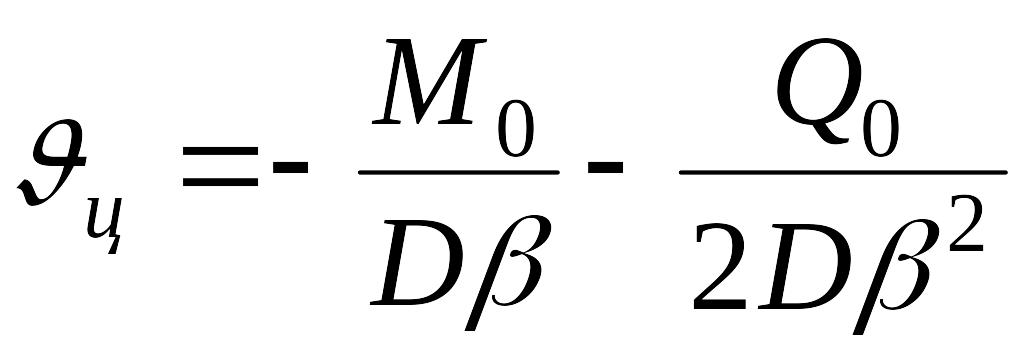Угол поворота нормали на краю днища определяется по одному из методов, рассмотренных ранее. В данном случае
,
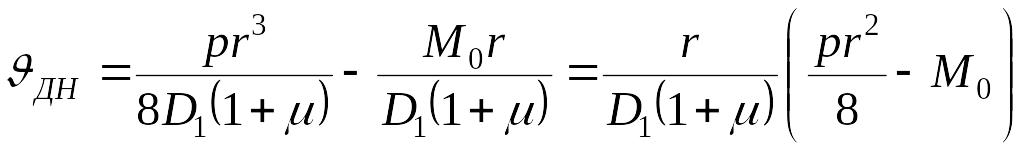где
— изгибная жесткость днища.
Уравнения совместности деформаций после подстановки в них значений перемещений принимают вид
;
.
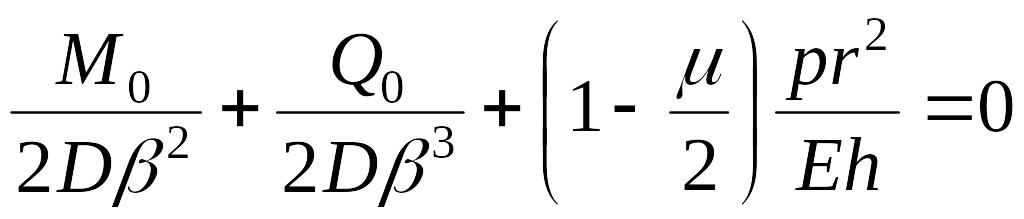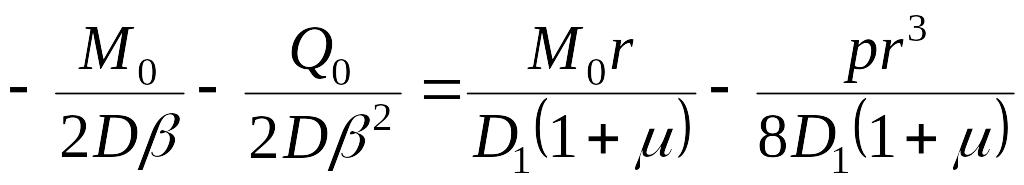При составлении уравнений совместности деформаций необходимо следить за правильностью знаков. В частности, в уравнении, выражающем равенство углов, момент должен входить в правую и левую части равенства обязательно с противоположными знаками.
Решение системы двух полученных уравнений при числовых значениях
;
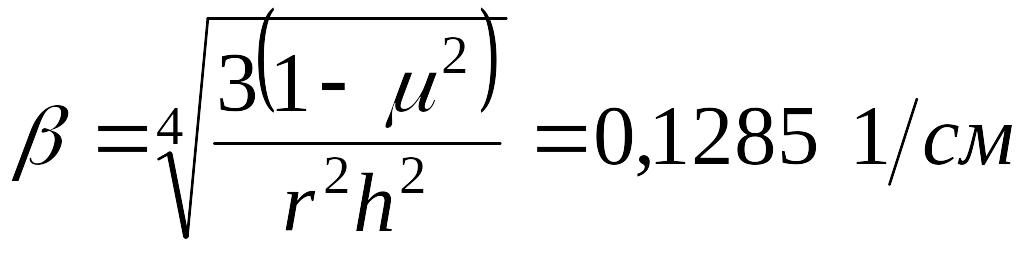
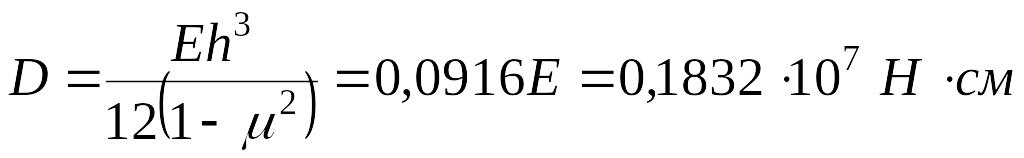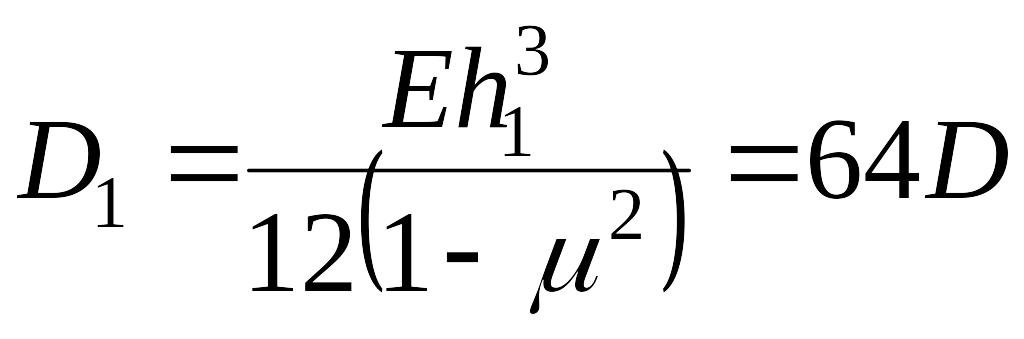
приводит к следующим результатам:
; 
.
Заметим, что при абсолютно жестком днище
.
Следовательно, за счет податливости днища изгибающий момент на краю цилиндра возрастает в данном случае более чем в 10 раз. Это объясняется тем, что днище, прогибаясь, как бы выворачивает край цилиндра.
Эпюры изгибающих моментов приведены на рис. 13.37.
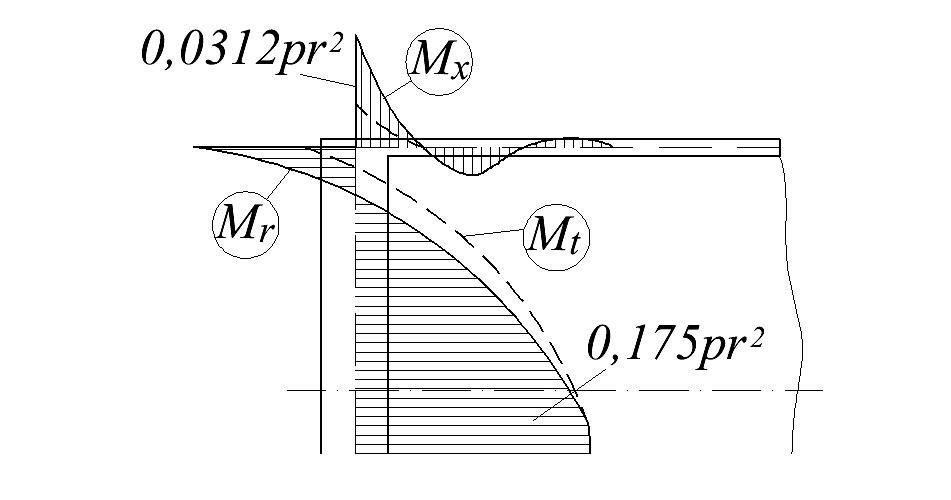
Рис. 13.37. Эпюры изгибающих моментов (к примеру 13.9)
Наибольшие напряжения в центре днища
.
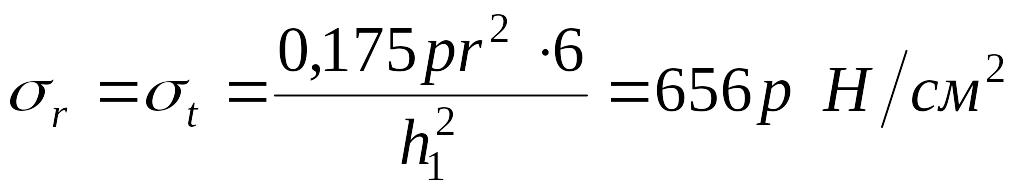Наибольшие напряжения в цилиндре — около края
;
.
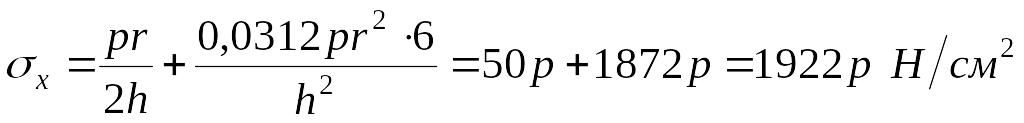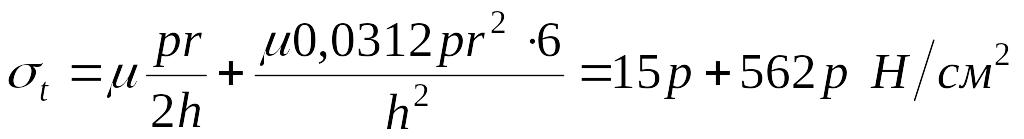Растягивающие напряжения в цилиндре вдали от края
;
.