Моментная теория осесимметричных цилиндрических оболочек

По с.В. Бояршинову

13.2.1 Вывод основных уравнений

Цилиндрические оболочки представляют собой наиболее распространенный вид оболочек вращения. Ввиду того, что теория цилиндрических оболочек значительно проще, чем оболочек другой формы, здесь эта теория рассмотрена отдельно от общего случая.

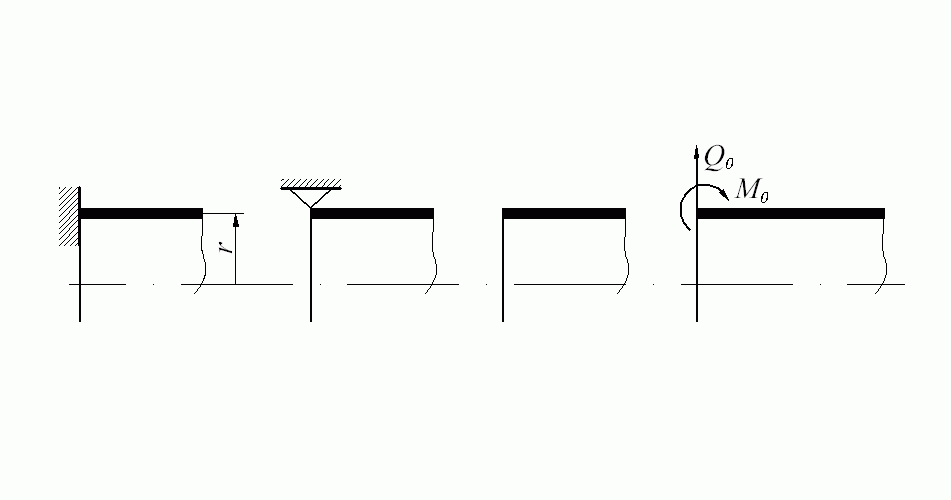
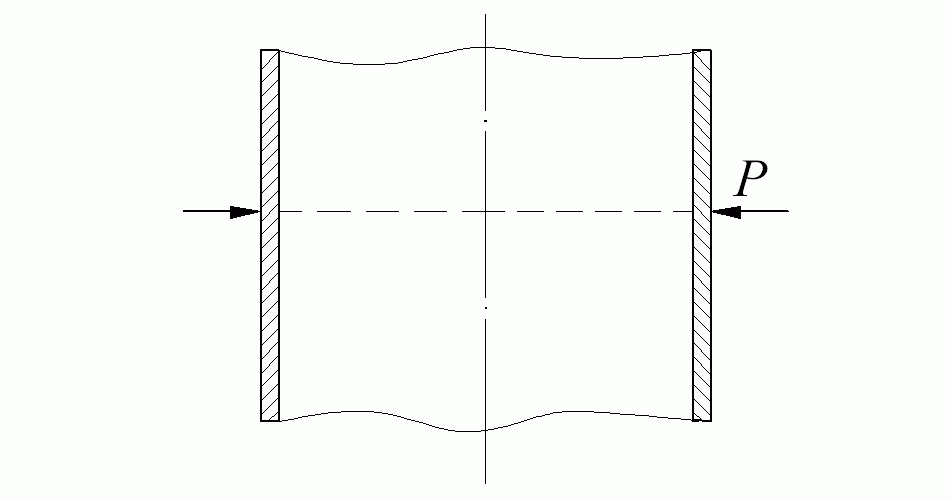
Осесимметричная изгибная деформация оболочки возникает в местах приложения внешних кольцевых нагрузок (рис. 13.1, а), а также в местах закрепления или сопряжения с другими конструктивными (рис. 13.1, б, в и г) элементами.

а	б
в	г

Рис. 13.27. Осесимметричная изгибная деформация оболочки

Теория осесимметричной деформации цилиндрических оболочек основана на гипотезах Кирхгофа — Лява, аналогичных гипотезам, используемым в теории изгиба пластин (1 – гипотеза неизменности нормалей и 2 – гипотеза о ненадавливании одного слоя оболочки на другой)

Указанные гипотезы выполняются достаточно удовлетворительно при условии, что толщина оболочки мала по сравнению с ее радиусом и что перемещения точек срединной поверхности малы по сравнению с толщиной. Если наибольшую допустимую погрешность расчета принять равной 5%, то к тонкостенным следует отнести оболочки, толщина которых не превышает 1/20 радиуса.

Кроме перечисленных гипотез и допущений примем, что материал оболочки однородный, изотропный и подчиняющийся закону Гука.

Введем обозначения:

и – радиус срединной поверхности оболочки и толщина ее стенки;

– толщина стенки цилиндра;

– координата, отсчитываемая от торца в направлении оси оболочки;

u, – перемещения произвольной точки срединной поверхности в осевом и радиальном направлениях.

	Выразим относительные деформации в произво-льном слое оболочки, расположенном на рас-стоянии от срединной поверхности через пере-мещения (будем считать положительным по на-правлению к центру). На рис. 13.28 изображен бесконечно малый эле-мент оболочки до и после деформации. Относительная деформа-ция волокна в осевом направлении:
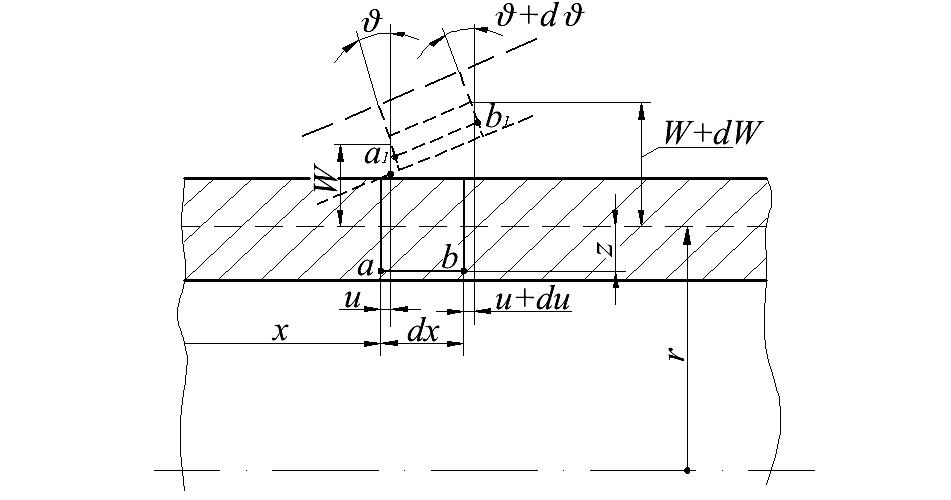
Рис. 13.28. Бесконечно малый элемент оболочки до и после деформации

(13.88)

где –– угол поворота нормали.

Относительная деформация в окружном направлении определяется как отношение приращения длины окружности, проходящей через произвольную точку , к первоначальной длине

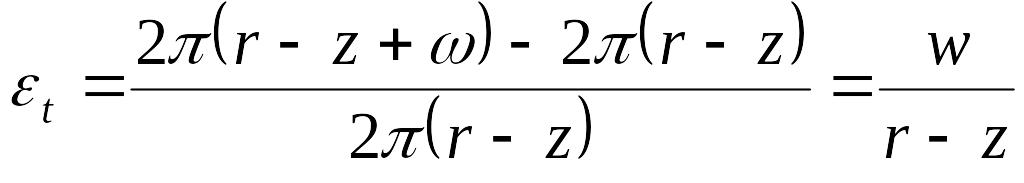
или, ввиду тонкостенности,

(13.89)

Перейдем от деформаций к напряжениям. При σ_z = 0 (см гипотезу 2) формулы закона Гука имеют вид

;

.

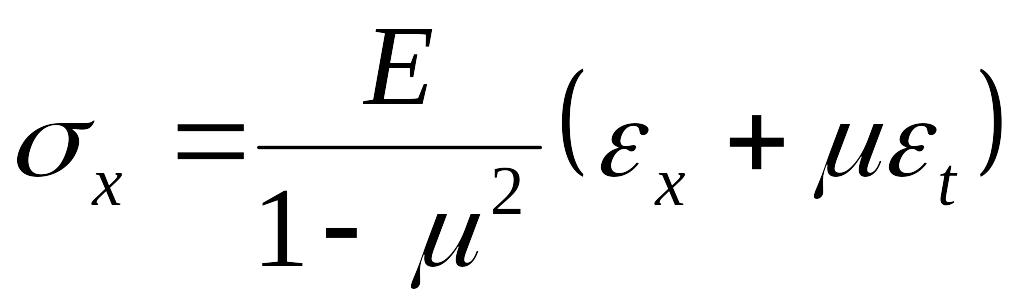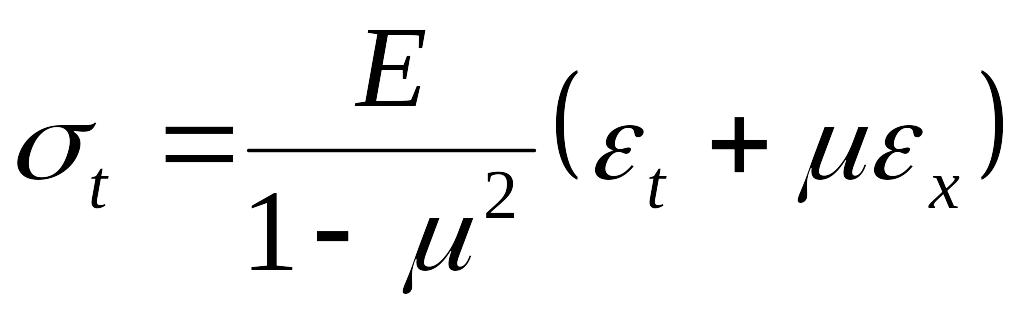Подставив в эти уравнения выражения деформаций (13.88) и (13.89), получим

;	(13.90)
.	(13.91)

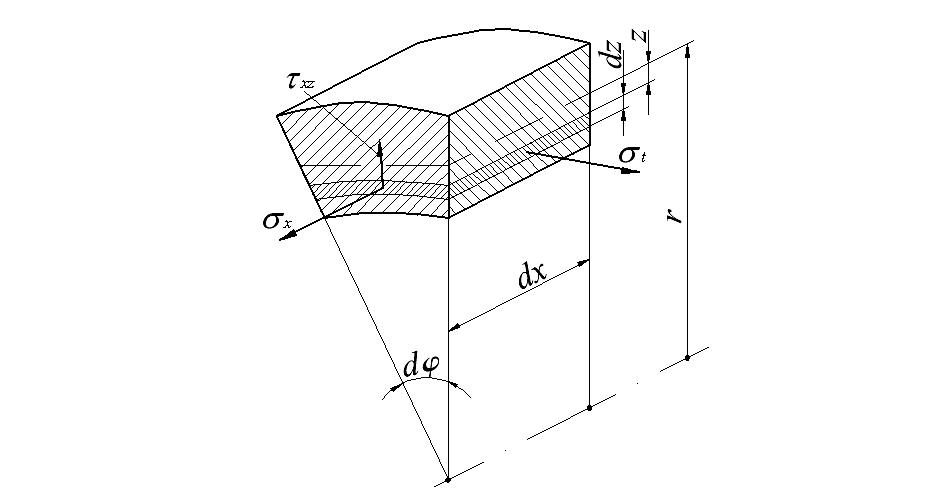
Напряженное состояние элемента оболочки показано на рис. 13.29.

Кроме напряжений σx и σt в произвольном слое возникает еще касательное напряжение τxz. Это нап-ряжение обычно бывает мало по сравнению с нормальными напряже-ниями и в расчетах на прочность не учитывается. Существенную роль иг-рает только равнодействующая касса-тельного напряжения τxz – попереч-ная сила Q, которая входит в урав-нения равновесия элемента оболочки. Перейдем от напряжений к внут-ренним силовым факторам. При ин-тегрировании по толщине оболочки напряжения σx и σt приводятся к нормальным силам Tx и Tt и изгибающим моментам Mx и Mt:

Рис.13.29. Напряженное состояние элемента оболочки

;	(13.92)
;	(13.93)
	(13.94)
,	(13.95)

где –– изгибная жесткость оболочки

.

(13.96)

Исключив из уравнений (13.92) и (13.93) перемещение , получим выражение окружного усилия T_t через и T_x:

.

(13.97)

Уравнения (13.94), (13.95) и (13.97) содержат пять неизвестных величин: усилия T_x и T_t , M_x и M_t и перемещения w.

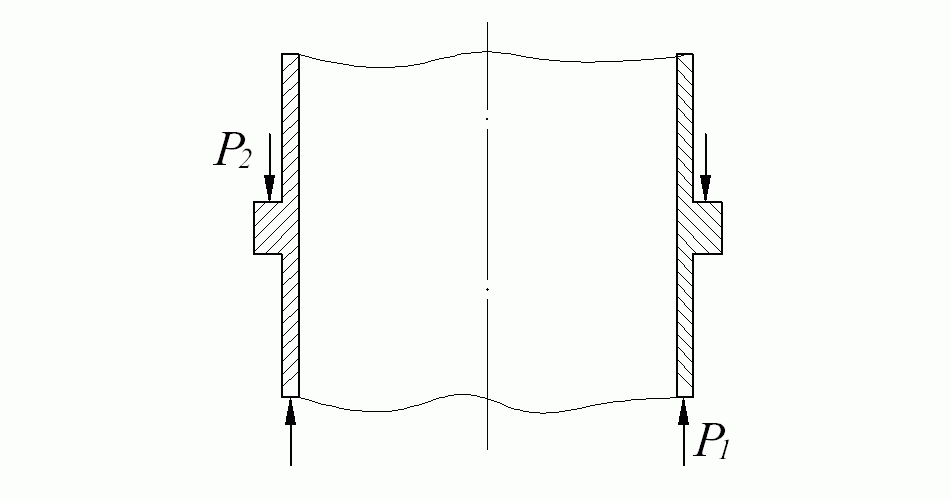
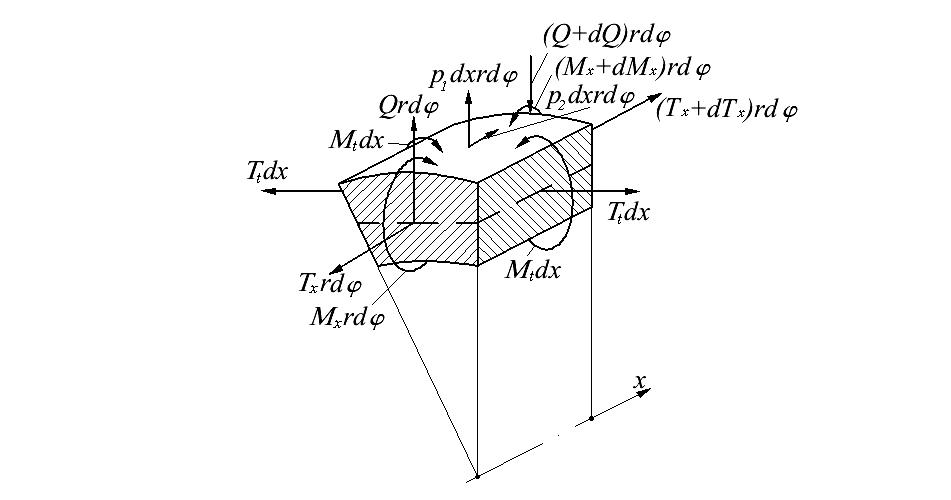
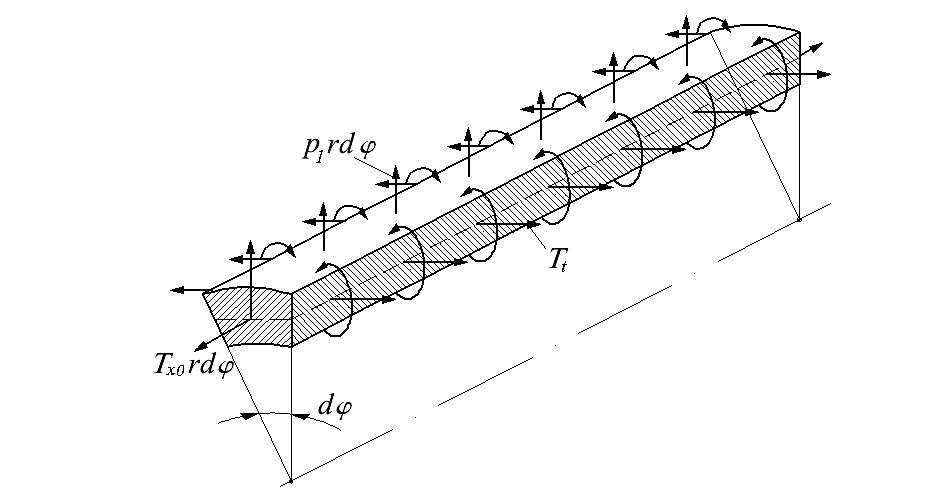
Чтобы получить недостающие уравнения, рассмотрим равновесие элементарного объема, выделенного из оболочки двумя продольными и двумя поперечными сечениями (рис. 13.30).

	Кроме сил Tx и Tt, моментов Mx и Mt на элемент действуют силы поверхностной нагрузки p1dxrdφ и p2dxrdφ (нагрузка p1, нормальная к поверх-ности, создается внутренним или наружным давлением; нагрузка p2, направленная вдоль оси оболочки, может возникнуть за счет сил тре-ния или за счет собствен-ного веса при вертикальном расположении оболочки). Из шести уравнений равно-весия в данном случае
Рис. 13.30. Равновесие элементарного объема

можно составить только три: уравнение проекций сил на направления и и уравнение моментов относительно оси у, касательной к окружности:

;	(13.98)
;	(13.99)
.	(13.100)

Остальные уравнения равновесия удовлетворяются тождественно. При решении полученной системы уравнений осевую силу T_x можно считать известной, так как она может быть определена заранее по уравнению (13.99). Действительно, умножив обе части уравнения на и проинтегрировав по x, найдем

.

Это уравнение представляет собой уравнение равновесия части оболочки, отсеченной по кругу . Первое слагаемое в правой части равенства представляет собой интеграл от поверхностных осевых сил; второе учитывает силы, приложенные к торцу.

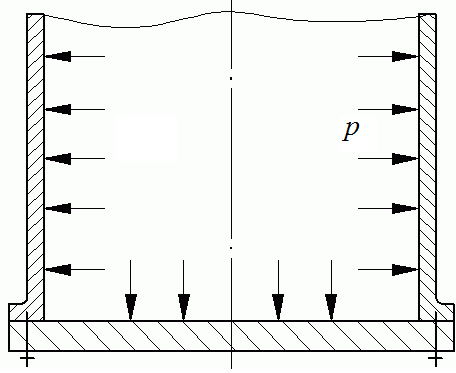
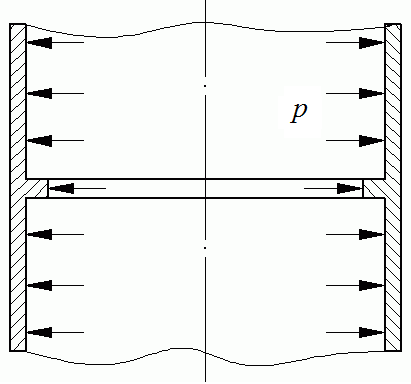
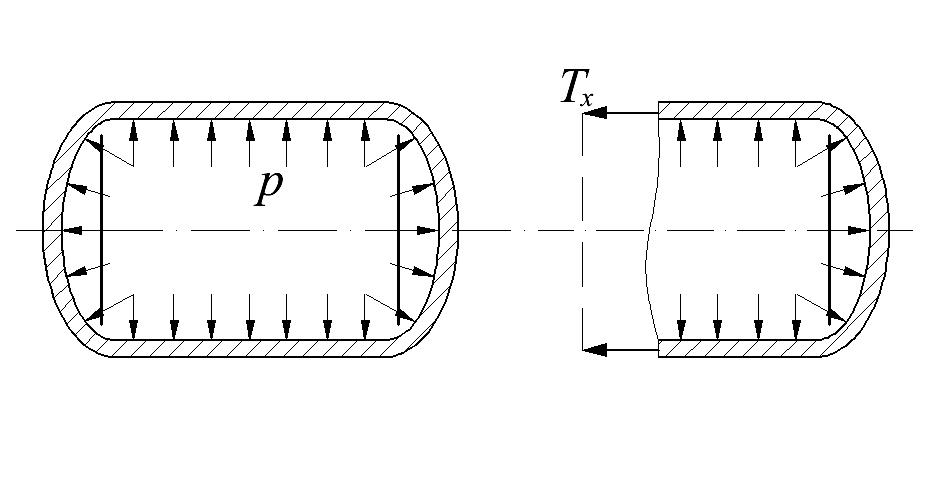
Если, например, цилиндрическая оболочка с днищем нагружена равномерным внутренним давлением (рис. 13.31, а), то, отделив часть оболочки (рис. 13.31, б), можно написать следующее уравнение равновесия:

,

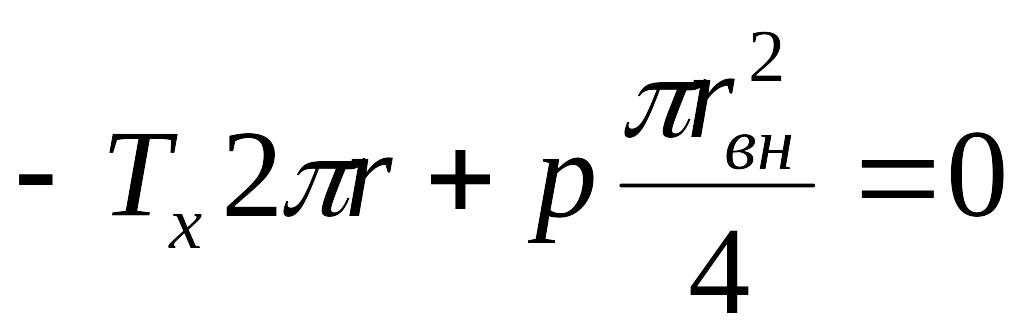откуда, считая r_вн = r , найдем T_x=pr/2.

а	б

Рис. 13.31. Нагрузка в виде равномерного внутреннего давления

Приведем систему уравнений деформаций и равновесия к одному уравнению с одним неизвестным. Из уравнения (13.100), с учетом равенства (13.94) следует

.

(13.101)

Выражения (13.97) и (13.101) подставим в уравнение (13.98), тогда

,

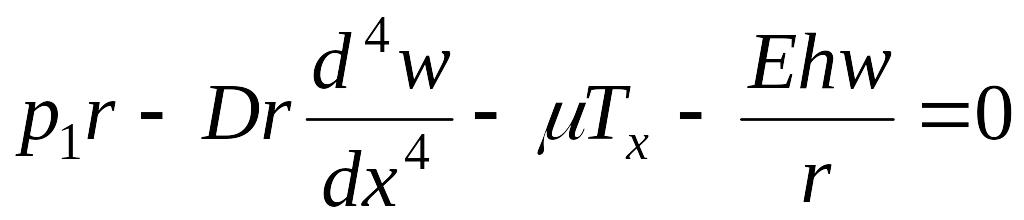или

,

(13.102)

где

.

(13.103)

Дифференциальное уравнение осесимметричной деформации цилиндрической оболочки (13.102) по своей структуре аналогично уравнению упругой линии балки, опирающейся на упругое основание. Эта аналогия не случайна. Если из оболочки вырезать полоску шириной (рис. 13.32), то ее можно рассматривать как брус, нагруженный поперечной нагрузкой .

	Oкружная сила Tt про-порциональна перемещению , т.е. она в данном случае играет роль реакции упругого основания. Запишем дифференци-альное уравнение упругой линии полоски как балки:
Рис. 13.32. Аналогия с брусом

Подставив в это уравнение выражение q и учтя зависимость (13.97), а также внеся значение момента инерции (множитель в знаменателе учитывает увеличение жесткости за счет взаимодействия с соседними полосками), и, используя обозначение жесткости (13.96), придем к дифференциальному уравнению (13.102).

Если функция , удовлетворяющая уравнению (13.102) и граничным условиям на краях, будет найдена, то по зависимостям (13.94) и (13.95) можно вычислить изгибающие моменты и по зависимости (13.97) – окруж-ную силу T_t. Напряжения σ_x и σ_t определяются через внутренние усилия

(13.104)

Эти формулы легко получить из уравнений (13.90) и (13.91) с учетом зависимостей (13.92) — (13.95).

Наибольшие напряжения возникают при :

;	(13.105)
.	(13.106)

Перейдем к интегрированию дифференциального уравнения (13.102). Общее решение уравнения представим в виде суммы общего решения однородного уравнения

(13.107)

и частного решения уравнения с правой частью (13.102). Решение однородного уравнения (13.107) ищем в виде . Подставив эту функцию в левую часть уравнения (13.20), получим характеристическое уравнение

,

из которого найдем

.

По правилам извлечения корней из отрицательных и мнимых чисел модуль числа k равен корню четвертой степени модуля подкоренного числа, т.е. , а аргумент числа k – аргументу подкоренного числа, деленному на показатель корня; т. е. , следовательно, k представляет собой комплексное число

.

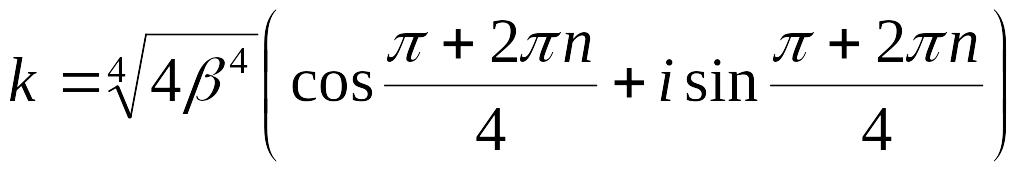Придавая значения 0, 1, 2, 3, получим четыре корня характеристического уравнения:

_.

Следовательно, общее решение однородного уравнения (13.107) имеет вид

или

(13.108)

где C_j – постоянные интегрирования (комплексные), .

Частное решение уравнения с правой частью зависит от закона распределения поверхностных нагрузок p₁ и p₂.

Обычно на практике нагрузки p₁ и p₂ или постоянны, или изменяются по x по линейному или квадратичному закону. Ограничиваясь только этими случаями и учитывая, что при указанных условиях и ( ), получим для w следующее выражение:

.

(13.109)

Для практических целей общее решение уравнения (13.107), представленное в виде (13.108), недостаточно удобно; поэтому его преобразуют к другому виду, причем, для длинных и для коротких оболочек это преобразование делается по-разному.

Остановимся на вопросе о постоянных интегрирования. Для определения постоянных необходимо использовать граничные условия на краях оболочки. На каждом краю обычно бывают заданы два условия.

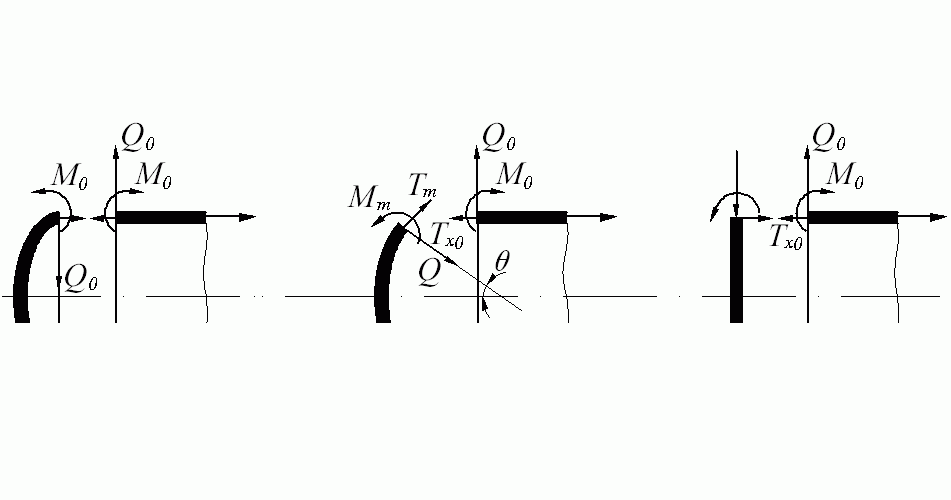
Если край жестко защемлен (рис. 13.33, а), то на краю должно быть:

Для шарнирно опертого края (рис. 13.33,б) и (так как M_x = 0).

Для свободного края (рис. 13.33, в)

_.

При нагружении края оболочки заданной силой и моментом (рис.13.33, г)

; .

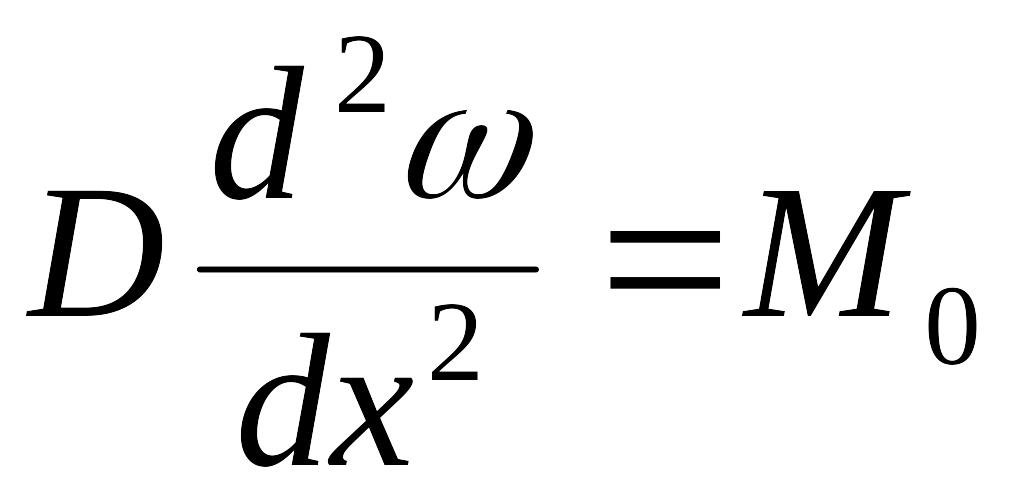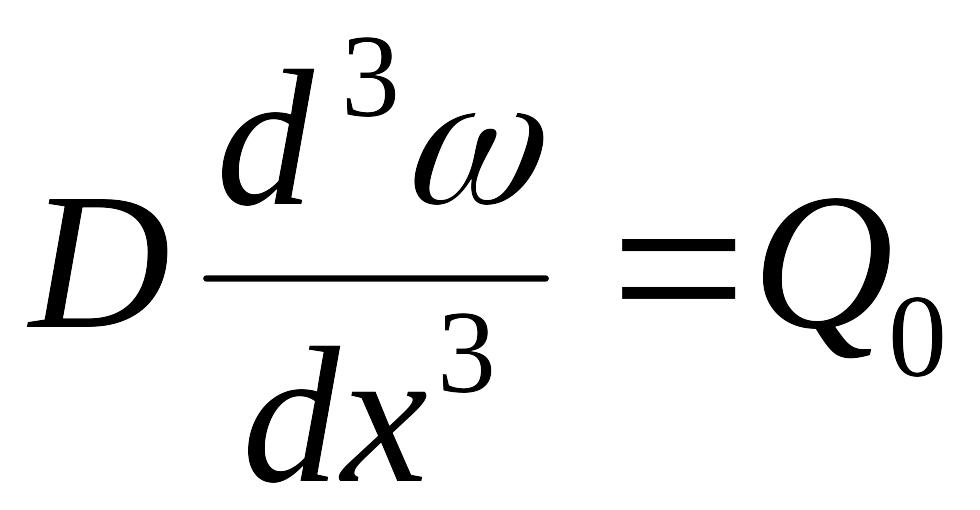В случае сопряжения цилиндрической оболочки с оболочкой другого типа (рис. 13.33, д, е) необходимо иметь четыре условия (для каждого края сопрягаемых оболочек требуется по два условия): равенство радиальных перемещений или равенство окружных деформаций ; равенство углов поворота нормали ; равенство моментов и ; равенство сил распора, т, е. радиальных составляющих внутренних сил:

Заметим, что равенство осевых составляющих внутренних сил не может быть использовано при определении постоянных, так как это условие уже использовано при определении усилия T_x.

При сопряжении цилиндрической оболочки с плоским днищем (рис. 13.33, ж) граничные условия несколько упрощаются, так как на основании допущения о нерастяжимости срединной поверхности пластины первое условие сопряжения принимает вид ; четвертое же условие становится ненужным.

а	б		в	г
д		е		ж

Рис. 13.33. Варианты граничных условий

Определение четырех постоянных интегрирования требует решения системы четырех уравнений с четырьмя' неизвестными. Однако практически всегда оказывается возможным построить решение так, что две постоянные определяются сразу, а остальные — в результате решения системы двух уравнений с двумя неизвестными.
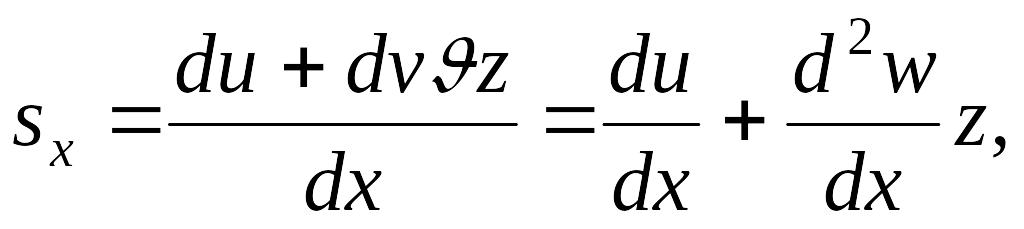
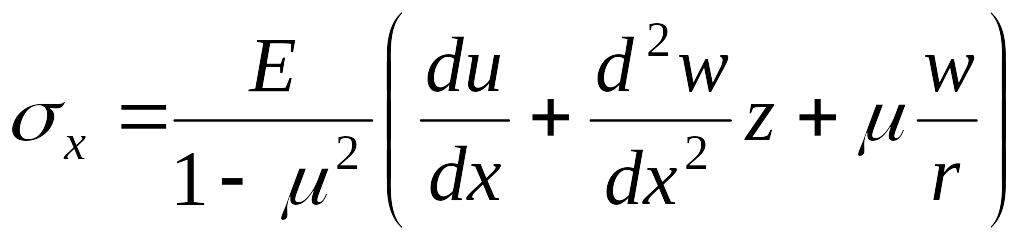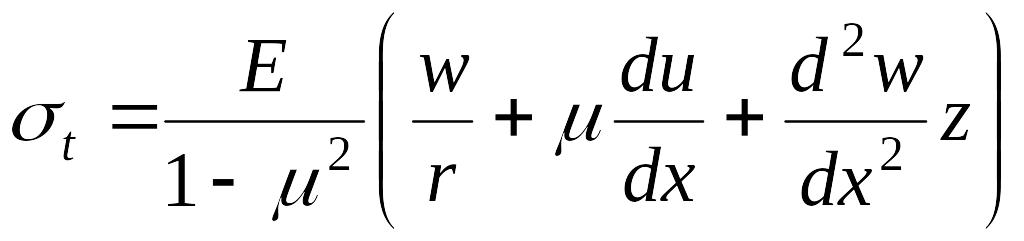
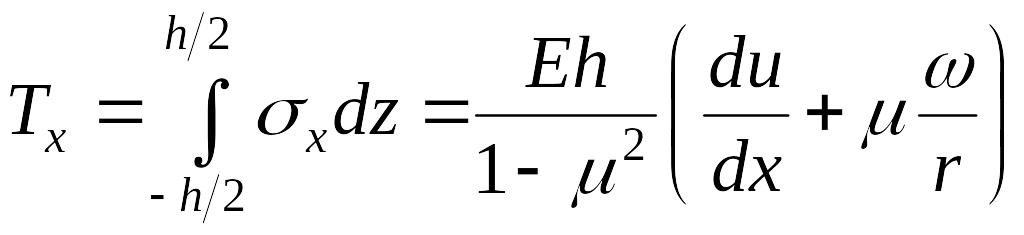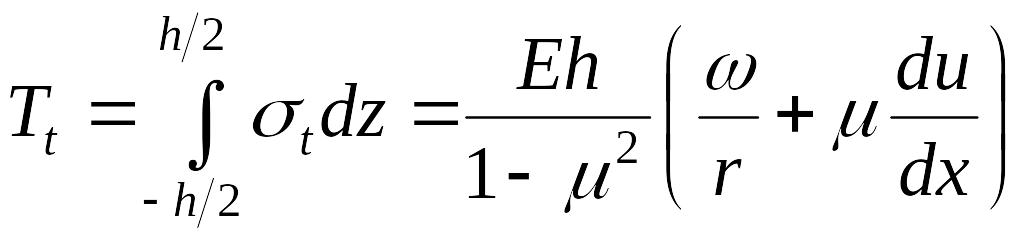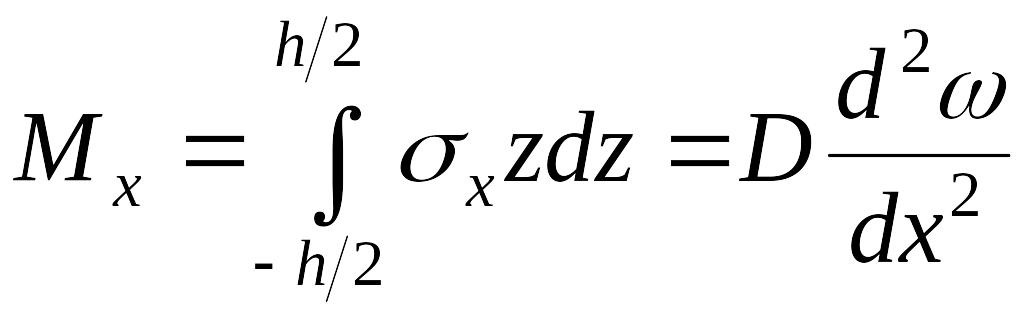
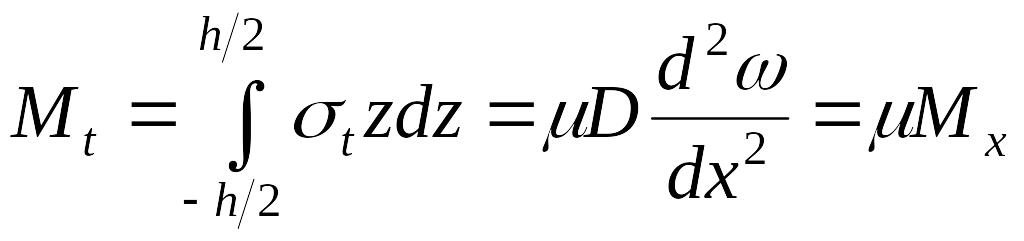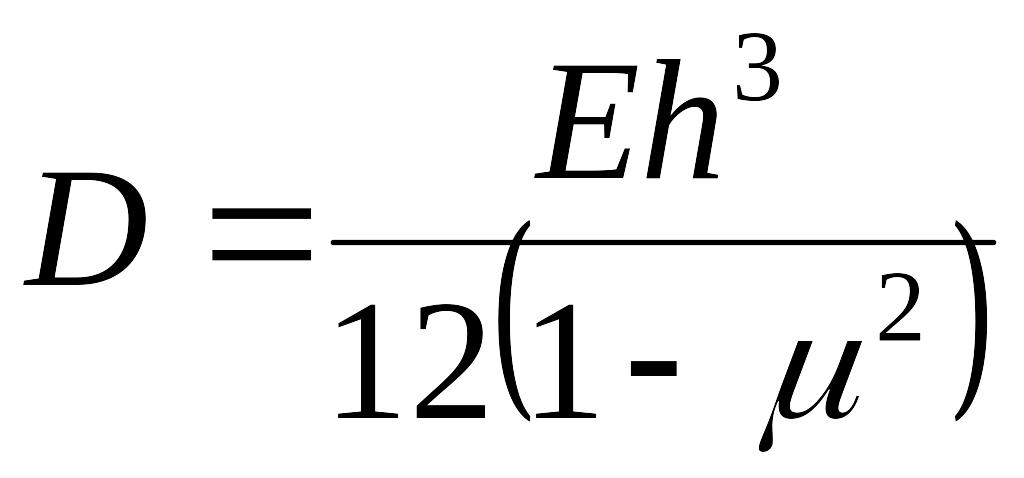
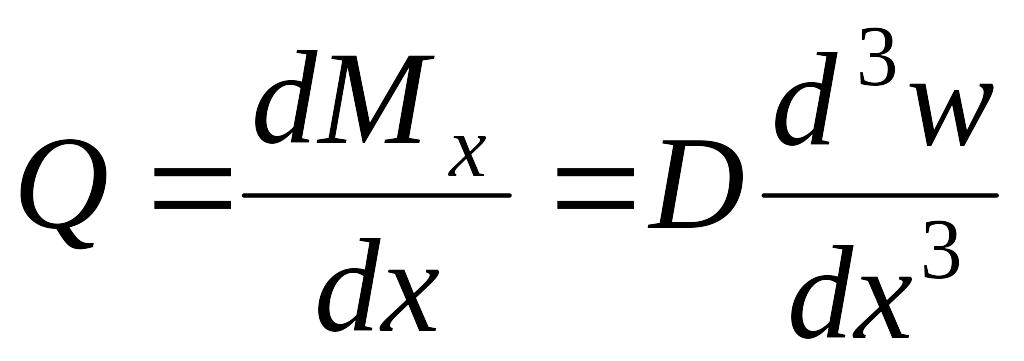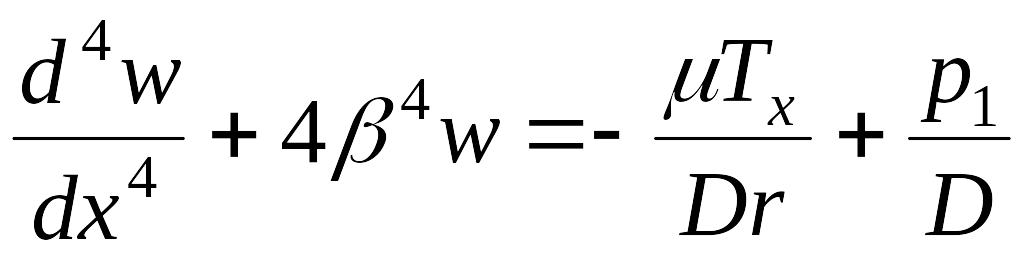