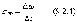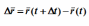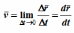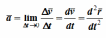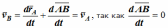14.Скорость точки

Скорость точки

1.2 Скорость точки Рассмотрим перемещение точки за малый промежуток времени  Δt: тогда  средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.

15.Ускорение точки

Ускорение точки

1.3 Ускорение точки Среднее ускорение   характеризует изменение вектора скорости за малый промежуток времени  Δt . Ускорение точки в данный момент времени Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.

16.Поступательные движения твердого тела

Поступательное движение твердого тела

Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению. Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.  Рис. 1.1 Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы. Доказательство.  Если выбрать две точки твердого тела А  и В  (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением Траектория точки А  – это кривая, которая задается функцией rA(t), а  траектория точкиB – это кривая, которая задается функцией rB(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы. Продифференцируем по времени выражение Получаем Рис. 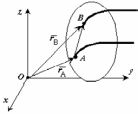1.2 Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы. Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

17.Вращательное движение твердого. Частные Случаи вращательного движения твердого тела.

 ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

9.1.

Поступательное движение

Поступательное движение - это такое движение твердого тела, при котором любая прямая соединяющая две точки тела, движется, оставаясь параллельной самой себе.

Поступательное движение нельзя смешивать с прямолинейным, так как при поступательном движении траектория может быть какой угодно.

Свойства поступательного движения характеризует следующая теорема:

Все точки твердого тела, движущегося поступательно, описывают одинаковые траектории и в каждый момент времени имеют одинаковые по модулю и направлению скорости и ускорения.

Пусть дано твердое тело совершающее поступательное движение относительно системы отсчета Oxyz (рис. 49  ).

Выберем произвольные точки A и В характеризующиеся радиус-векторами   в момент времени t.

Проведем вектор  , тогда

Так как тело движется поступательно, то траекторию точки А получим из траектории точки В параллельным смещением всех точек на отрезок  .

Продифференцируем уравнение (9.1.1):

Взяв производную от (9.1.3), получаем

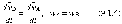
т.е. скорости и ускорения всех точек твердого тела одинаковы.

9.2.

Вращательное движение твердого тела

Вращательным называют такое движение твердого тела, при котором две какие-нибудь точки принадлежащие телу, остаются во все время движения неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки лежащие на оси так же неподвижны.

Чтобы определить положение вращающегося тела, введем две плоскости, проходящие через ось вращения (рис. 50  ) А - плоскость неподвижная; В - плоскость связанная с телом и вращающаяся с ним; DE - ось вращения, совпадающая с осью z.

Теперь в любой момент времени положение тела будет определяться углом   между плоскостями А и В или углом поворота тела, положительным, если вращение происходит против часовой стрелки, и отрицательным в противном случае. Закон вращательного движения

Угол поворота обычно измеряют в радианах.

Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость   и угловое ускорение  .

Если за промежуток времени   тело совершает поворот на угол  , то средняя угловая скорость будет численно равна

Угловой скоростью тела в данный момент t называется величина, к которой стремится средняя угловая скорость 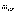 , если   стремится к нулю.

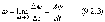
Угловая скорость твердого тела является первой производной от угла поворота по времени.

Размерность: [радиан/время]; [1/время]; [1/сек = ].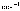

Угловую скорость можно изображать вектором. Вектор угловой скорости   направляют по оси вращения в ту сторону, откуда вращение видно против хода часовой стрелки.

Если угловая скорость не является постоянной величиной, то вводят еще одну характеристику вращения - угловое ускорение.

Угловое ускорение характеризует изменение угловой скорости тела с течением времени.

Если за промежуток времени   угловая скорость получает приращение 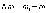 , то среднее угловое ускорение равно