12.Условия Пространственной системы произвольно расположенных сил
Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.
Отсюда вытекает условие равновесия произвольной пространственной системы сил.
В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю
R = 0, Mo = 0.
В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю
ΣFkx = 0, ΣFky = 0, ΣFkz = 0,
Mx(Fk) = 0, My(Fk) = 0, Mz(Fk) = 0.
13.Центр тяжести. Способы определение центра тяжести. Координаты центра тяжести плоского тела и составленных сечений.
Центр тяжести
Центр тяжести тела - точка приложения силы тяжести (равнодействующей гравитационных сил).
Центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс.
Определение центра тяжести
Определение центра тяжести произвольного тела путем последовательного сложения сил, действующих на отдельные его части,— трудная задача; она облегчается только для тел сравнительно простой формы.
Пусть тело состоит только из двух грузов с массами m1 и m2, соединенных стержнем (рис. 126). Если масса стержня мала по сравнению с массами m1 и m2, то ею можно пренебречь. На каждую из масс действует сила тяжести:
P1=m1g, Р2=m2g;
обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы уже знаем, равнодействующая двух параллельных сил приложена в точке О, которая определяется из условия
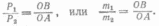
Следовательно, центр тяжести делит расстояние между двумя массами в отношении обратном отношению масс. Если это тело подвесить в точке О, оно останется в равновесии.
Определение координат центра тяжести
Способы определения координат центра тяжести Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
1 Аналитический (путем интегрирования).
2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела). 4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны
Рисунок 1.8
5 Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9 |
Центр тяжести однородных плоских тел
(плоских фигур)
Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать: V = Ah, где А — площадь фигуры, h — ее высота.
Тогда после подстановки в записанные выше формулы получим:
; 
; 
,
где Ак — площадь части сечения; хк, ук — координаты ЦТ частей сечения.
Выражение 
называют
статическим моментом площади (Sy.).
Координаты центра тяжести сечения можно выразить через статический момент:
; 
; 
; 
.
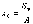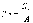Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
Определение координат центра тяжести плоских фигур
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты. Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.3: а) — круг; б) — квадрат, прямоугольник; в) — треугольник; г) — полукруг).
