47.Изгибающие моменты. Правила построение эпюр изгибающий момент.

Изгибающий момент Mx в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.

Правило знаков для Mx: условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде:

Следует отметить, что при использовании правила знаков для Mx в указанном виде, эпюра Mx всегда оказывается построенной со стороны сжатых волокон балки.

3.5. Построение эпюр изгибающих моментов и поперечных сил.

Рассмотрим пример построения эпюр поперечных сил Q и изгибающих моментов M_x.

1. Изображаем расчетную схему (рис. 3.9, а).

2. Определяем реакции опор. Первоначально выбираем произвольное направление реакций (рис. 3.9, а) 

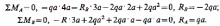
Так как реакция R_B с минусом, изменяем выбранное направление на противоположное (рис. 3.9, б), а про минус забываем.

Проверка: 

Y = 0,  R_A - 2qa + R_B - qa = qa - 2qa + 2qa - qa = 0.

3. Расчетная схема имеет три силовых участка.

I участок АС: 0 < z₁ < a. Начало координат выбираем в крайней левой точке А. Рассмотрим равновесие отсеченной части бруса (рис. 3.10).

В сечении возникают внутренние усилия:

поперечная сила 

Q = qa = const

и изгибающий момент 

M_x = qa * z₁ при z₁ = 0 M_x = 0; при z₁ = a M_x = qa².

II участок CB: 0 < z₂ < 2a. Начало координат перенесено в начало участка С (рис. 3.11).

На этом участке 

при z₂ = 0 Q = qa, M_x = -qa²;

при z₂ = 2 Q = -qa, M_x = qa². 

 

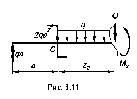
На 2-м участке в уравнении моментов аргумент z₂ имеет 2-ю степень, значит эпюра будет кривой второго порядка, т.е. параболой. На этом участке поперечная сила меняет знак (в начале участка +qa, а в конце -qa), значет на эпюре M_x будет экстремум в точке, Q = 0. Определяем координату сечения, в котором экстремальное значение M_x, приравнивая нулю выражение поперечной силы на этом участке. 

Определяем величину экстремального момента (с учетом знака):

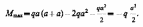
III учаток BD: 0 < z₃ < a. Начало координат на третьем участке помещено в крайней правой точке (рис. 3.12). 

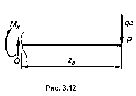
Здесь Q = qa = const; M_x = -qa*z₃; при z₃ = 0 M_x = 0; при z₃ = a M_x = -qa².

4. Строим эпюры Q и M_x (рис. 3.13, б и в). 

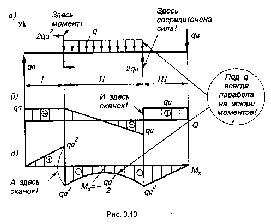
5. Проверка построения.

48.Диффиринциальная зависимость интенсивностью распространению нагрузки, поперечной силой и изгибающим моментом.

Дифференциальные зависимости между распределенной нагрузкой, поперечной силой и изгибающим моментом:

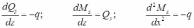
Дифференциальные зависимости используются для контроля правильности построенных эпюр поперечных сил  и изгибающих моментов  .

Помимо дифференциальных зависимостей существуют интегральные зависимости, получаемые из формул дифференциальных зависимостей. Например, изгибающий момент равен определенному интегралу по длине участка балки. Используя интегральную зависимость между изгибающим моментом и поперечной силой и аналитическое выражение поперечных сил, можно построитьэпюру изгибающих моментов, не определяя выражение для них.

В формулах дифференциальных и интегральных зависимостей распределенная нагрузка (q) положительна, если направлена вниз.