44.Полярный момент инерции. Полярный момент инерции для круга, для кольца.

Полярный момент инерции

[0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&veaction=edit&vesection=0"править | 0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&action=edit&section=0"править исходный текст]

Материал из Википедии — свободной энциклопедии

Не следует путать с 0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8"Момент инерции.

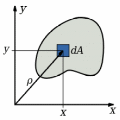
Схема к вычислению полярного момента инерции

Поля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ² (в 0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82"полярной системе координат), взятая по всей площади сечения. То есть:

Эта величина используется для прогнозирования способности объекта оказывать сопротивление 0%9A%D1%80%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5"кручению. Она имеет размерность единиц длины в четвёртой степени (м⁴, см⁴) и может быть лишь положительной.

Для площади сечения, имеющей форму 0%9A%D1%80%D1%83%D0%B3"круга 0%A0%D0%B0%D0%B4%D0%B8%D1%83%D1%81"радиусом r полярный момент инерции равен:

Если совместить начало 0%94%D0%B5%D0%BA%D0%B0%D1%80%D1%82%D0%BE%D0%B2%D0%B0_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82"декартовой прямоугольной системы координат 0 с полюсом полярной системы (см. рис.), то

потому что  .

Полярный момент - инерция - круг

Страница 1

Полярный момент инерции круга в два раза больше осевого момента инерции круга относительно оси, проходящей через его центр. [1]

Вычислим полярный момент инерции круга относительно его центра, а также момент инерции относительно центральной оси. [2]

Определим полярный момент инерции круга относительно его центра. [3]

Зная полярный момент инерции круга относительно центра, легко найти его момент инерции относительно диаметра. Поскольку осевые моменты инерции одинаковы для всех диаметров, из ( А. [4]

Вычислим полярный момент инерции круга относительно его центра, а также момент инерции относительно центральной оси. [5]

Чему равны полярные моменты инерции круга и кольца относительно их центров. [6]

Сначала определяем полярный момент инерции круга. [7]

Установим формулу для определения полярного момента инерции круга. [8]

Рассмотрим теперь, как вычисляется полярный момент инерции круга относительно его центра ( рис. А. [9]

Исходя из этого определения, вычислим полярный момент инерции круга. [10]

В предыдущей главе без вывода были приведены формулы для полярных моментов инерции круга и кругового кольца; выведем эти формулы. [11]

Чему равны осевые моменты инерции круга и кольца относительно осей, проходящих через их центры тяжести. Чему равны полярные моменты инерции круга и кольца относительно их центров. [12]